Основные теоремы электростатики и магнитостатики

Основные уравнения, описывающие свойства статических электрических и магнитных полей, приведены в табл. 4.1.

Таблица 4.1

Закон	Электростатика	Магнитостатика
Теорема Гаусса	Источники электрического поля – заряды	Магнитных зарядов не существует
Теорема о циркуляции поля	Потенциальность электрического поля	Источники магнитного поля – токи (вихревой характер магнитного поля)
Материальные уравнения	,

Постоянные электрическое и магнитное поля имеют различную физическую сущность: источниками электростатического поля являются заряды, источниками магнитного поля – постоянные токи; электростатическое поле является потенциальным, а магнитное – вихревым (соленоидальным).

Система уравнений электростатики не содержит никаких характеристик магнитного поля, как и система уравнений магнитостатики не содержит никаких характеристик электрического поля, т.е. уравнения электростатики и магнитостатики являются независимыми, а электрические и магнитные поля, описываемые этими уравнениями, существуют отдельно одно от другого.

Однако известны явления, которые указывают на взаимосвязь электрических и магнитных полей. Например, появление магнитного поля вокруг движущегося заряда. В данном случае электрический заряд является источником электрического и магнитного полей. Другой пример – явление электромагнитной индукции.

Взаимосвязь и взаимопревращаемость электрических и магнитных полей в природе были установлены Дж. Максвеллом, обобщившим труды Фарадея и создавшим теорию электромагнитного поля. В основе этой теории лежит система уравнений Максвелла.

4.2. Вихревое электрическое поле.
Первое уравнение Максвелла

Индукционный ток в неподвижном проводнике появляется при изменении магнитного потока. Это свидетельствует о появлении в контуре сторонних сил, приводящих в движение заряды. Сторонние силы обусловлены возникающим в контуре особым вихревым электрическим полем , циркуляция которого по замкнутому контуру отлична от нуля и равна ЭДС индукции:

.

С учетом закона Фарадея для электромагнитной индукции (3.1) получаем:

. (4.1)

Максвелл предположил, что изменяющееся со временем магнитное поле приводит к появлению в пространстве электрического поля (рис. 4.1), независимо от того присутствует в этом пространстве проводящий контур или нет. Наличие контура лишь позволяет обнаружить это электрическое поле по возникновению индукционного тока в проводнике.

В общем случае электрическое поле 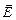слагается из потенциального поля , циркуляция которого по замкнутому контуру равна нулю, и вихревого поля :

, где .

Первое уравнение Максвелла в интегральной форме:

. (4.2)

Интеграл в левой части берется по произвольному замкнутому контуру, в правой части – по произвольной поверхности, опирающейся на этот контур.

4.3. Ток смещения.
Взаимопревращаемость электрических и магнитных полей.
Второе уравнение Максвелла

Максвелл предположил, что не только переменные магнитные поля являются источниками электрических полей, но и переменные электрические поля являются источниками магнитных полей. 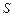Согласно гипотезе Максвелла, изменяющееся во времени электрическое поле создает в окружающем пространстве вихревое магнитное поле, циркуляция которого по любому замкнутому контуру, равна скорости изменения потока электрической индукции через поверхность , ограниченную этим контуром, эта величина получила название тока смещения:

.

Смысл введения этой величины можно пояснить следующим опытом (рис. 4.2). Конденсатор, подключенный к источнику постоянного тока, представляет собой разрыв цепи для тока проводимости, поэтому в такой цепи ток не течет. При этом в конденсаторе имеется электрическое поле, индукция которого .

Если конденсатор подключить к источнику переменного тока, то, как показывает опыт, в цепи будет течь переменный ток. Его существование можно объяснить только тем, что в пространстве между обкладками ток проводимости замыкается током смещения, поскольку теперь . В этом случае конденсатор перестает представлять собой разрыв цепи.

В соответствии с гипотезой Максвелла полный ток в проводнике складывается из тока проводимости 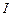и тока смещения , каждый из которых является источником своего магнитного поля так, что общее магнитное поле, существующее вокруг проводника, есть. Следовательно, .

Если контур интегрирования охватывает несколько проводников с током, то в соответствии с теоремой о циркуляции магнитного поля:

, (4.3)

где – плотность тока, протекающего через поверхность .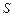

Уравнение (4.3) является вторым уравнением Максвелла в интегральной форме. Физический смысл этого уравнения заключается в том, что источником магнитного поля являются токи проводимости и токи смещения. Следовательно, одним из основных свойств токов смещения является способность создавать магнитное поле. В отличие от токов проводимости токи смещения не выделяют тепло.

По аналогии с плотностью тока проводимости величину называют плотностью тока смещения.

Третье уравнение Максвелла

Третье уравнение Максвелла в интегральной форме совпадает с теоремой Гаусса для магнитной индукции:

. (4.4)

Интегрирование производится по произвольной замкнутой поверхности 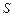. Это уравнение показывает, что в природе не существует «магнитных зарядов».