Силовые линии магнитного поля

Магнитные поля так же, как и электрические, можно изображать графически при помощи силовых линий. Магнитной силовой линией, или линией индукции магнитного поля, называют линию, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции поля.

а)	б)	в)

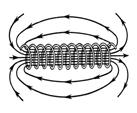
Рис. 1.2. Силовые линии магнитного поля прямого тока (а),

кругового тока (б), соленоида (в)

Магнитные силовые линии так же, как и электрические, не пересекаются. Их прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) величине магнитной индукции магнитного поля в данном месте.

На рис. 1.2, а приведены силовые линии поля прямого тока, которые представляют собой концентрические окружности, центр которых расположен на оси тока, а направление определяется правилом правого винта (ток в проводнике направлен на читателя).

Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. На рис. 1.2, б показаны силовые линии магнитного поля кругового тока. Магнитное поле соленоида представлено на рис. 1.2, в.

Силовые линии магнитного поля замкнуты. Поля, обладающие замкнутыми силовыми линиями, получили название вихревых полей. Очевидно, что магнитное поле – вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

В электростатическом поле силовые линии всегда разомкнуты: они начинаются и заканчиваются на электрических зарядах. Магнитные силовые линии не имеют ни начала, ни конца. Это соответствует тому, что в природе нет магнитных зарядов.

Закон Био–Савара–Лапласа

Французские физики Ж. Био и Ф. Савар провели в 1820 г. исследование магнитных полей, создаваемых токами, текущими по тонким проводам различной формы. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и установил зависимость, которая получила название закона Био–Савара–Лапласа.

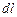Согласно этому закону, индукция магнитного поля любого тока может быть вычислена как векторная сумма (суперпозиция) индукций магнитных полей, создаваемых отдельными элементарными участками тока. Для магнитной индукции поля, создаваемого элементом тока длиной , Лаплас получил формулу:

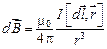, (1.3)

где 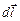– вектор, по модулю равный длине 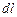элемента проводника и совпадающий по направлению с током (рис. 1.3); 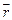– радиус-вектор, проведенный от элемента 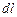в ту точку, в которой определяется 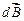; 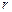– модуль радиуса-вектора .

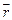Модуль выражения (1.3) определяется формулой:

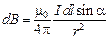, (1.4)

где 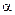– угол между векторами 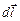и .

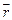Магнитное поле прямого тока

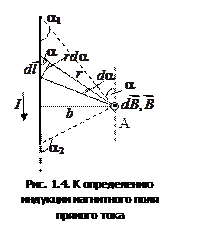Применим формулу (1.4) для вычисления магнитной индукции поля прямого тока, т.е. поля, создаваемого током, текущим по тонкому прямому отрезку провода (рис. 1.4). В произвольной точке 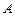, удаленной от оси проводника на расстояние 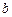, векторы 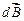от всех элементов тока имеют одинаковое направление («на читателя»). Поэтому сложение векторов 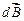можно заменить сложением их модулей. Из рис. 1.4 видно, что

, .

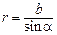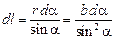Подставив эти выражения в формулу (1.4), получим:

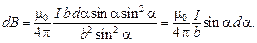
Угол 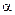для всех элементов отрезка прямого тока изменяется в пределах от 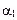до 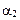, поэтому

.

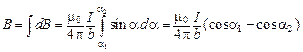Для случая прямого провода бесконечной длины 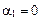, 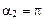и, согласно последнему выражению, магнитная индукция определяется формулой:

.
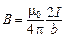