Программный комплекс reactop и его применение для разработки моделей технологических объектов
 |
Программный комплекс ReactOp предназначен для решения задач разработки математических моделей технологических объектов, в которых происходит превращение исходных продуктов в конечные за счет различных химических превращений, и использования моделей для последующего анализа поведения объекта.
Программная система подразделена на ряд подпрограмм, называемых experts или Wizard, предназначенных для решения ряда задач общей проблемы.
Первая подпрограмма или
Wizard - «Модель» (Model) предназначена для разработки модели технологического объекта. Она содержит набор моделей объектов, учитывающих структуру потоков технологических сред, и включает в себя следующие объекты:
1. Аппараты периодического действия (с одновременной загрузкой всех компонентов (batch reactor-br) c различными видами режимов теплообмена: адиабатический режим, заданная температура без учета теплообмена, режимы с теплообменом. Эти тепловые режимы используются и для всех других типов аппаратов.
2. Аппараты полупериодического действия, когда часть компонентов загружается в аппарат, а часть дозируется с задаваемой скоростью (semi batch reactor-sbr).
3. Проточные аппараты идеального смешения с упомянутыми в пункте 1 тепловыми режимами для жидкой и газовой фазы (continuous stirred tank reactor for liquid –cstrl, continuous stirred tank reactor for gases - cstrg).
4. Каскад проточных аппаратов идеального смешения для 2-х и 3-х аппаратов (2cstrl, 3cstrl).
5. Проточные аппараты идеального вытеснения с различными тепловыми режимами для жидких потоков реагентов (plug flow reactor for liquid –pfrl).
6. Проточные аппараты идеального вытеснения для потоков реагентов в газовой фазе с учетом переменной скорости потока за счет изменения плотности реакционной среды за счет изменения давления и температуры (plug flow reactor for gases –pfrg)
7. Нестандартные модели, которые могут быть созданы пользователем за счет модификации стандартных моделей.
Для построения конкретной модели объекта нужно кликнуть мышью на Model Wizard и войти в эту подпрограмму.
На экране дисплея высвечивается меню, содержащее различные возможности построения модели
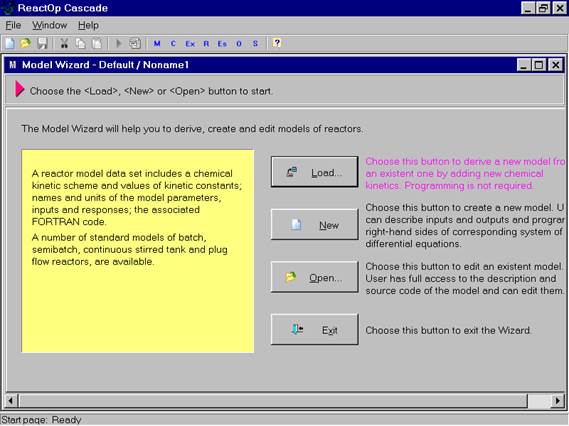 |
Load- загрузить существующую из выше перечисленных моделей, описывающих гидродинамику потоков. К этой модели необходимо добавить схему реакций, происходящих в аппарате и условия теплообмена и модель будет готова.
New- построить новую нестандартную модель
Open- открыть уже созданную модель для дальнейшей работы
Exit - выйти из данной подпрограммы.
Для выбора желаемого действия необходимо кликнуть мышью по соответствующему пункту меню.
Например, мы хотим построить модель объекта с использованием банка существующих моделей. Для этого мы подводим мышь к названию Load и открываем соответствующую страницу.
На экране появляется следующая страница. Нажав команду Browse, мы входим в список моделей.
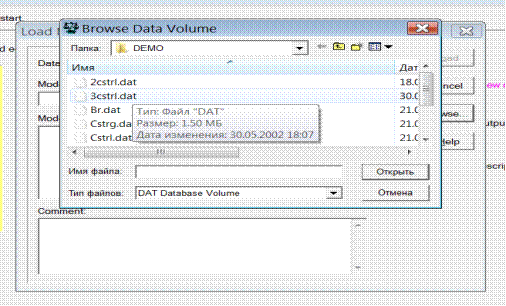
Выбрав в списке моделей, например Br реактор периодического действия мы получаем на экране его схематическое изображение и уравнения математической модели в общем виде. Это изображено на следующей картинке экрана.
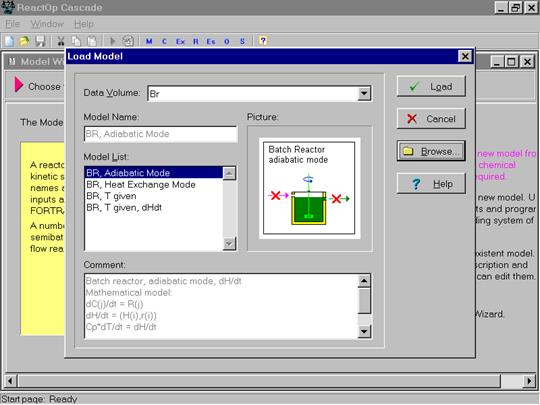
Теперь необходимо нажать команду Load (загрузить), чтобы ввести в модель схему реакций. На экране появляются окна для загрузки схемы реакций.
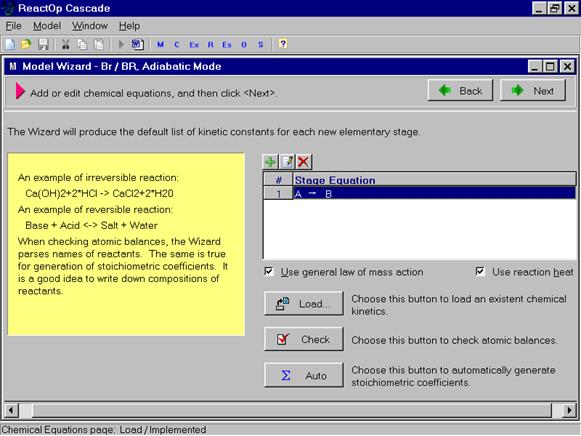
Над окном для изображения схемы реакций имеются три кнопки 1-я кнопка(крестик) –добавить реакцию, 2-я кнопка – редактировать и 3-кнопка удалить реакцию. Нажав 1-ю или 2-кнопку мы входим в окно, позволяющее записывать реагенты в правой и левой частях уравнения и вид протекания стадии
-обратимая (reversible) и необратимая (irreversible). Последовательно вводятся уравнения всех химических стадий.
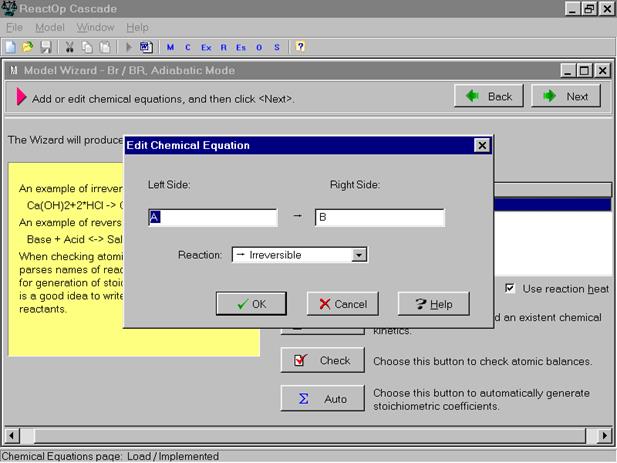
После ввода химических стадий нажимается кнопка OK и мы переходим на следующую страницу, предлагающую ввести кинетические константы и тепловые эффекты для записанных стадий процесса.
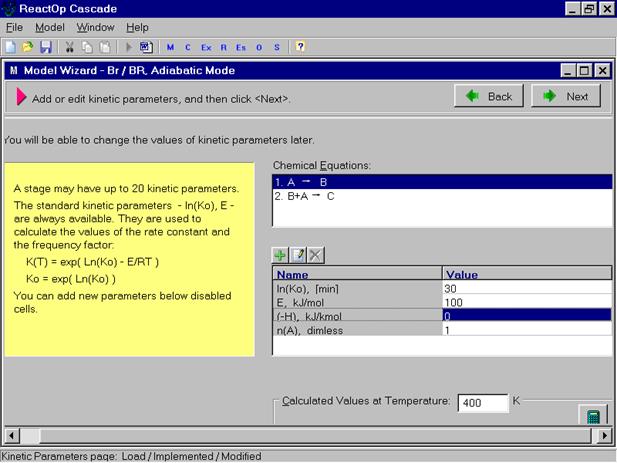
Здесь показываются значения параметров для каждой стадии и имеются три кнопки, позволяющие добавить, отредактировать, или убрать соответствующие параметры для отмеченной стадии. Отметив необходимое действие, мы получаем окно для редактирования параметров.
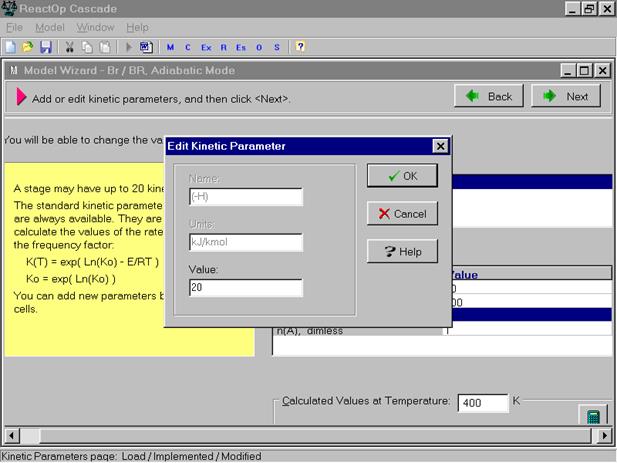
После ввода всех необходимых параметров модели, мы нажимаем команду Next и выходим в следующее окно сохранения модели.
Нажав команду save as (сохранить как) мы попадаем в следующее окно меню, в котором нам предоставляется возможность создать папку (Volume) для хранения модели и присвоить ей собственное имя. Эта картинка представлена на следующем изображении экрана.
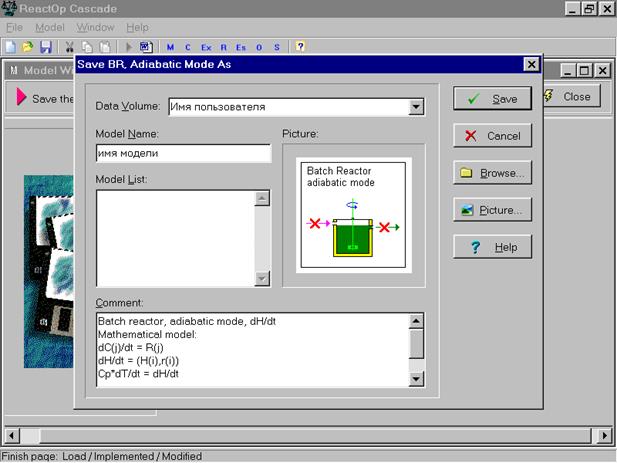
Таким образом, модель готова для решения. С ней могут быть проделаны следующие действия:
1. Решение ее при заданных начальных условиях переменных состояния и условиях работы аппарата. Это выполняется при использовании Simulation wizard
2. Создание таблицы экспериментальных данных по результатам наблюдения за объектом моделирования в соответствии со структурой созданной модели. Это выполняется при использовании Experiment wizard
3. Решение задачи идентификации модели объекта путем поиска параметров модели по экспериментальным данным. Это выполняется при использовании Estimation wizard.
4. Решение задачи определения оптимальных условий функционирования объекта по критерию оптимизации, сформулированному из переменных состояния, путем поиска кинетических констант. Это делается при использовании Estimation Wizard.
В качестве 1-го действия необходимо решить уравнения модели при заданных условиях функционирования объекта. Это эквивалентно проведению наблюдениий над объектом с помощью его математической модели. Для выполнения этого действия необходимо войти в Simulation Wizard.
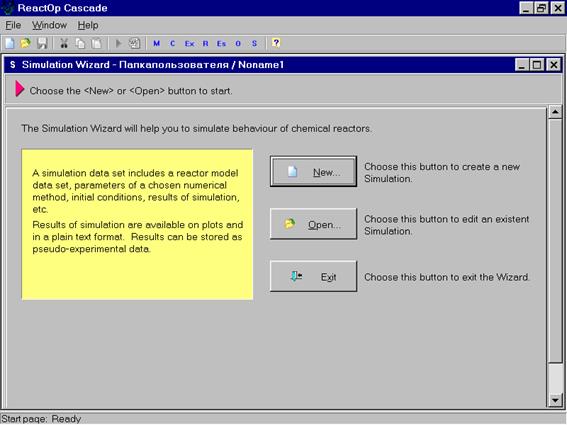 |
Далее необходимо нажать кнопку New. Появляется окно создания новой задачи моделирования, с индикацией списка созданных моделей.
Когда мы решаем задачу первый раз мы, естественно, создаем новую задачу. Щелкнув мышью по команде New, мы входим в меню создания задачи моделирования.
Здесь предоставляется список имеющихся моделей, из которых мы выбираем необходимую модель. При первом решении это будет одна модель. Выбрав эту модель, мы входим в окно задания условий моделирования.
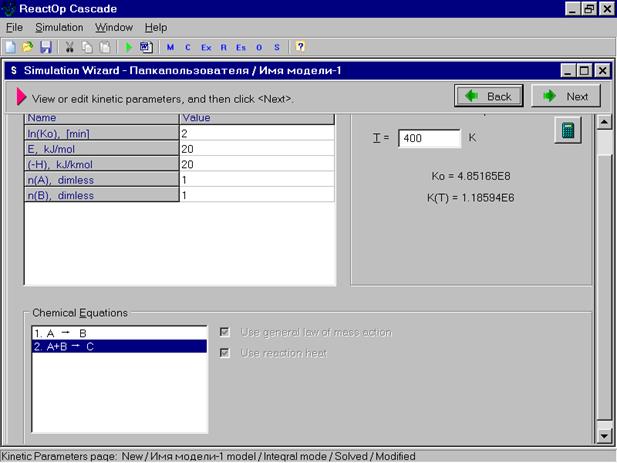
В этом окне мы можем отредактировать параметры модели и перейти к заданию начальных условий
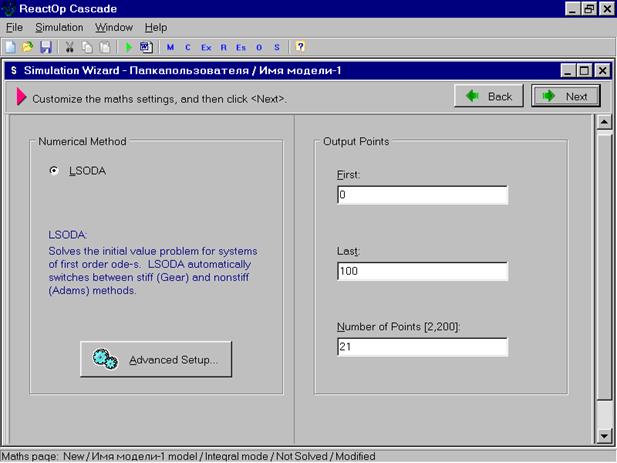
В этом окне выбирается длительность времени процесса, количество точек выдачи результатов, а также уточняются математические методы решения и задаваемая точность решения.
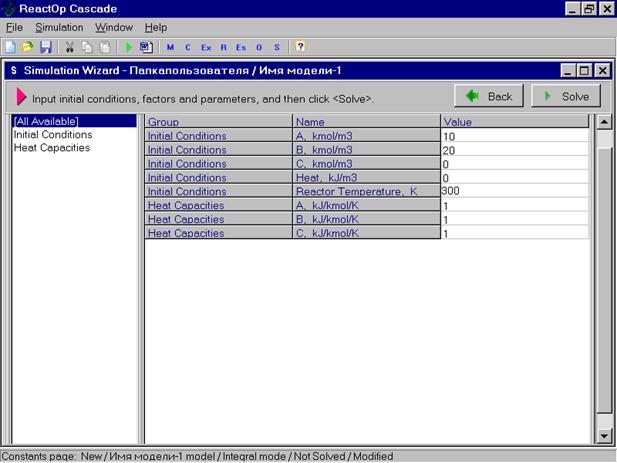
В следующем окне задаются начальные условия моделирования по всем переменным состояния, описываемым в модели и свойства компонентов.
Задав все необходимые условия, мы нажимаем команду Solve ( решать) и осуществляем решение уравнений модели. В результате решения мы получаем картину концентрации компонентов. Результаты представлены в следующем окне.
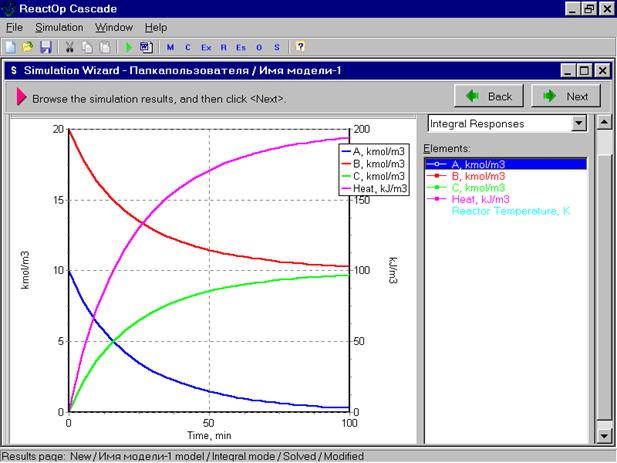 |
После окончания решения нажимается команда Next и мы попадаем в следующее окно, предоставляющее возможность сохранить результаты, как результат моделирования, как модель или как экспериментальные данные для последующего использования. В верхней строке меню имеется кнопка, помеченная знаком W(Word), нажатие которой позволяет создать отчет, включающий в себя описание модели, условий моделирования и результаты расчетов в виде таблиц. Имеется возможность скопировать рисунок с помощью правой кнопки мыши и присоединить его к отчету.
Далее мы можем приступить к решению задачи создания таблицы экспериментальных данных в соответствии со структурой модели. Для этого лучше всего сохранить вначале результаты моделирования как эксперимент. В результате будет автоматически сформирована таблица экспериментальных данных, которую можно затем откорректировать.
Для решения задачи создания таблиц экспериментальных данных входим в главное меню системы и нажимаем мышью команду Experiment wizard.
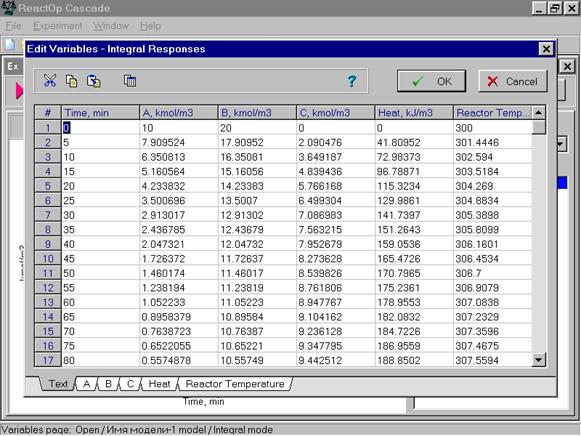
Мы попадаем в окно этой подпрограммы, предлагающее создать новую таблицу для интегральных или дифференциальных откликов, или открыть уже существующий файл.

Поскольку мы уже имеем первый вариант экспериментальных данных, мы нажимаем команду Open.
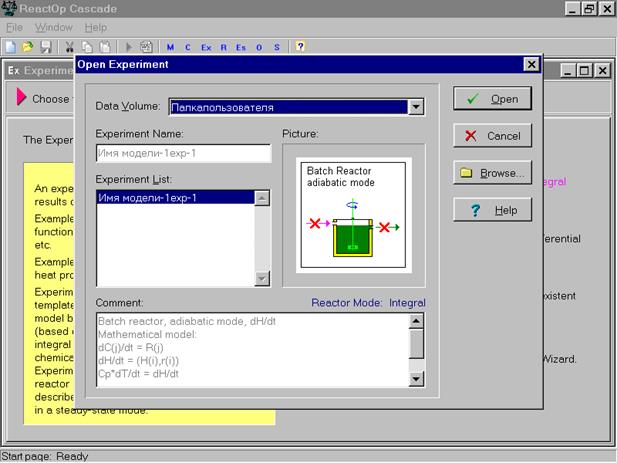
Высвечивается название файла экспериментальных данных, название используемой модели, ее схема и математическая модель. Отмечаем необходимый файл и нажимаем команду Open ( открыть), Выбранный файл экспериментальных данных открывается для редактирования, т.е. фактически для ввода экспериментальных данных в форме, соответствующей структуре созданной модели.
На экране высвечиваются введенные результаты моделирования.
Кликнув мышью по графику, мы входим в таблицу экспериментальных данных, внизу которой обозначены все переменные.
Поочередно нажимаем мышью на все переменные и вводим вместо расчетных экспериментальные данные в соответствующие точки по времени ( или по длине).Это показано далее для переменной, соответствующей концентрации реагента А.
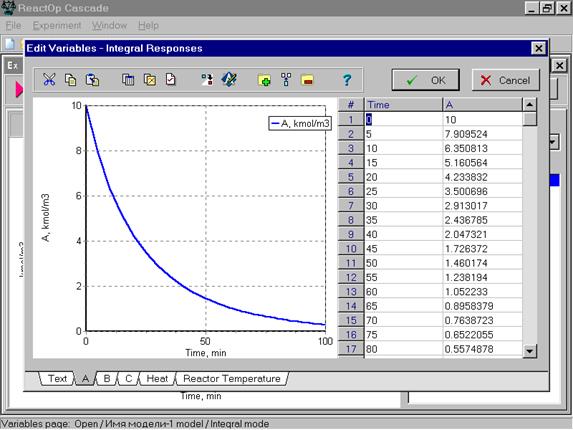 |
После ввода фактических экспериментальных данных по соответствующей переменной, нажимаем команду OK и переходим к следующей переменной. После ввода всех экспериментальных данных, нажимаем команду Next, и выходим в окно задания начальных условий данного эксперимента.
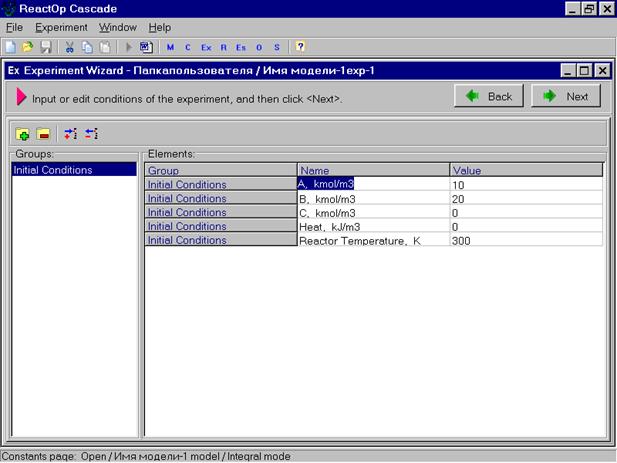
Задав начальные условия данного эксперимента, переходим в следующее окно сохранения результатов.
Сохраняем результаты корректировки под другим именем в своей папке данных.
После этого мы можем приступать к решению задачи 3 –определения параметров математической модели по экспериментальным данным из условия минимального рассогласования между результатами расчета и моделирования. В качестве функции рассогласования используется выражение определяемое формулой (3). Для решения этой задачи входим в главное меню системы и нажимаем команду входа в Estimation wizard.
Открывается окно Estimation wizard и предлагается также три возможности
New –создать новую задачу оценки параметров
Open – открыть существующую задачу
Exit- выйти из подсистемы оценки параметров
Для первого решения задачи нажимаем команду New и попадаем в окно, показывающее список моделей. Выбираем созданную модель и нажимаем команду OK. Попадаем в следующее окно, предлагающее загрузить экспериментальные данные.
Нажимаем команду Load Experiment (загрузить эксперимент) и попадаем в окно со списком экспериментальных файлов.
Выбираем необходимый файл экспериментальных данных и нажимаем команду Load. Появляется окно экспериментальных данных со списком всех переменных, описываемых моделью. Выбираем те переменные, по которым есть результаты измерений и которые будут использоваться при формировании функции рассогласования s(kj), определяемой формулой (3). Подводим к соответствующей переменной мышь и дважды ее нажимаем. Соответствующая переменная помечается цветом и знаком ˅. После этого нажимается команда Next и мы попадаем в окно выбора метода поиска констант и настройки точности вычислений .
После выбора метода ( отметив мышью выбранный метод) и установки точности ( входом в окно Advanced Setup) мы переходим в следующее окно задания условий поиска.
Далее задаются неопределенные в модели параметры теплоемкости компонентов и мы попадаем в окно определения начального приближения параметров модели.
Записав соответствующие схемы реакций, мы кликаем мышью по надписи next и переходим к следующей странице программы.
На следующей странице программа предлагает записать первое приближение для параметров модели – lnk0 и E – натуральный логарифм предэкспоненциального множителя константы скорости реакции и энергию активации для каждой стадии записанных химических превращений.
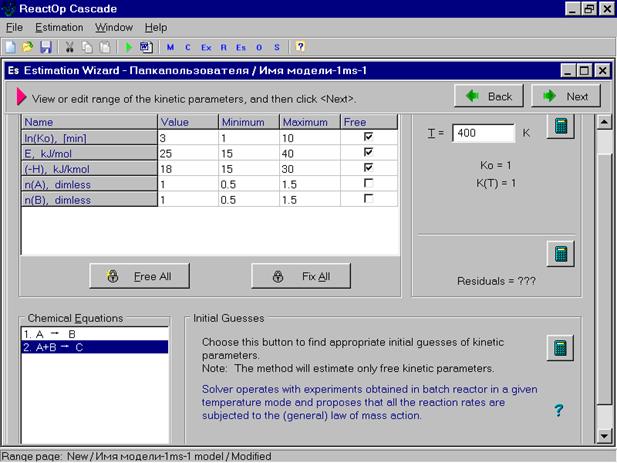
В правой колонке таблицы отмечается, какие параметры могут варьироваться, а не отмеченные параметры фиксируются на заданном уровне. Кнопка Residuals позволяет вычислить величину рассогласования при заданном начальном приближении. Нажав кнопку Next, мы попадаем в следующее окно.
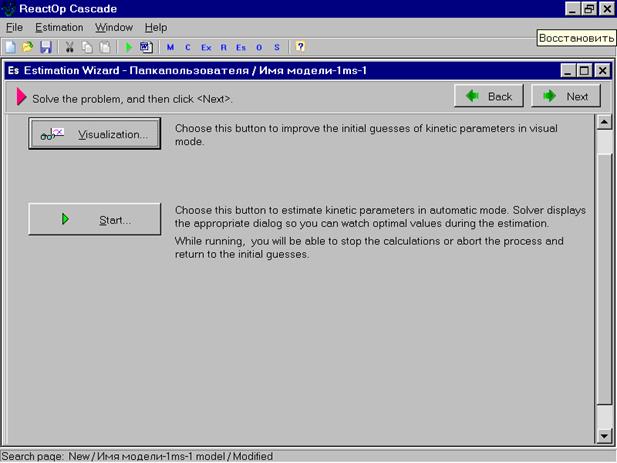
Клавиша Visualisation (визуализация) позволяет просмотреть, как описываются экспериментальные данные при начальном приближении параметров. На следующей картинке окна показано описание моделью концентрации реагента А при начальном приближении параметров.
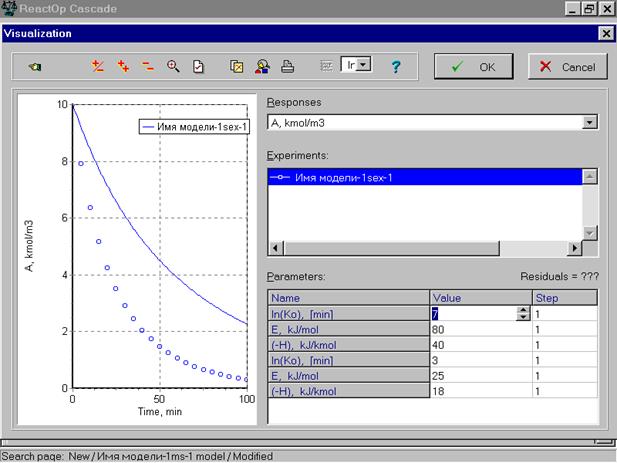
В правом верхнем окошке находится список переменных модели, которые можно перелистать и просмотреть, как описывается каждая переменная.
Из рисунков видно, что при начальном приближении параметров экспериментальные данные описываются неудовлетворительно. Поэтому мы активизируем мышкой команду Start, которая включает процедуру поиска по варьируемым параметрам модели. Текущие результаты поиска отображаются в следующем окне.
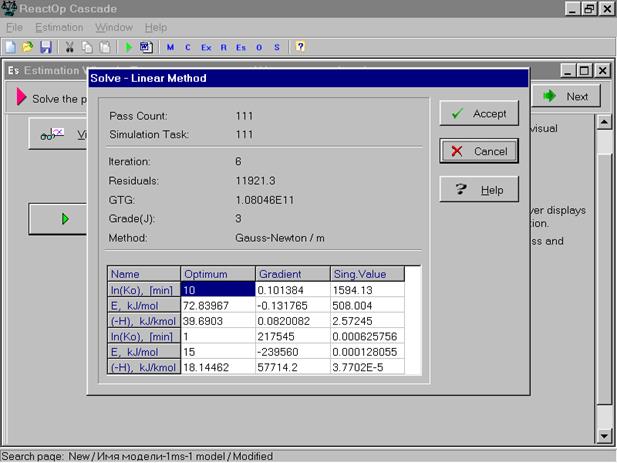
В окне отображаются результаты поиска в виде количества шагов поиска, текущей величины градиента функции, текущих значений параметров и значений частных производной функции по каждому параметру модели.
После завершения процедуры поиска по заданной точности нахождения экстремума, высвечивается окно окончания поиска с результатами параметров в точке минимума и величиной рассогласования между результатами моделирования и эксперимента. Эта величина характеризует качество описания. Окно представлено на следующей картинке.
Надпись The solving is over означает, что поиск закончен. Нажав клавишу OK, мы получаем возможность визуально посмотреть качество описания всех переменных моделью, как это показано на картинке следующего окна.

В окне приведено качество описания переменной А и найденные параметры модели. Если качество описания удовлетворительно, можно нажать клавишу OK и перейти в окно результатов статистического анализа полученных результатов. Окно представлено на следующей картинке.
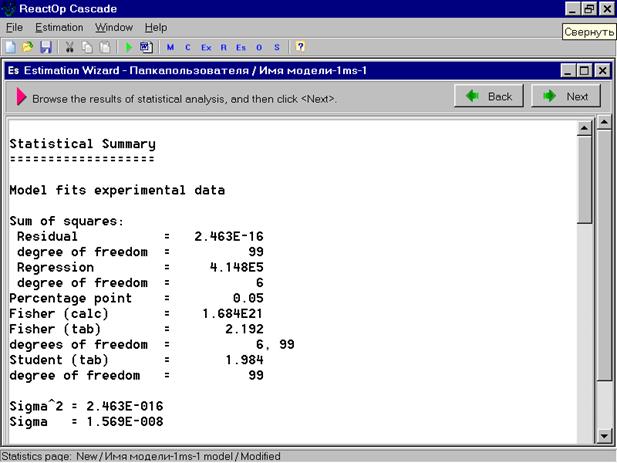
Надпись Model fits experimental data означает, что модель адекватно описывает экспериментальные данные. Выбрав в верхней строчке меню кнопку со знаком W можно сформировать отчет о результатах поиска. К отчету можно присоединить необходимые графики сопоставления расчетных и экспериментальных данных. Для этого нужно скопировать выбранный рисунок с помощью кнопки Copy as picture и вставить рисунок в отчет. Отчет затем можно сохранить в виде файла и распечатать для составления отчета.
Работа №1 по курсу «Математическое моделирование» По результатам наблюдения за технологическим аппаратом построить математическую модель аппарата и исследовать поведение аппарата в заданном диапазоне температур.
Объект исследования – Реактор периодического действия, в котором протекают последовательные реакции 1-го порядка. A®P®F
1. Организовать наблюдение за объектом и получить экспериментальные данные в виде зависимости концентраций компонентов от времени. Для наблюдения за объектом создать его модель в программном комплексе ReactOp Cascade..
2. Создать математическую модель реактора.
3. Используя математическую модель определить кинетические параметры
4. Провести моделирование процесса в исследованном диапазоне температур и определить для каждой температуры время достижения максимальной концентрации компонента Р и значение его определить на графике.
5. Определить максимальную конверсию в целевой продукт и построить зависимость максимальной конверсии от температуры.
6. Составить отчет о выполненной расчетно- графической работе. Представить графики сопоставления расчетных и экспериментальных данных, графики моделирования при 5-ти температурах из заданного диапазона температур. Построить графики зависимость максимальной конверсии от температуры и времени достижения максимальной конверсии от температуры.
Порядок выполнений работы.
В качестве объекта наблюдения использовать математическую модель реактора, созданную в программном комплексе ReactOp,
Для этого выполнить следующие действия:
1. Открыть программный комплекс ReactOp,
2. Войти в подпрограмму Model wizard, выбрать команду Load.
3. Нажать кнопку Browse
4. Войти на диске C в папку Program Files, CISP, ReactOp Cascade, Demo и выбрать модель Br..
5. В перечне тепловых режимов работы выбрать режим Br, T given.
6. В окне химических реакций ввести схему реакций и нажать кнопку Next.
7. В появившемся окне кинетических параметров ввести кинетические параметры:
Для 1 реакции lnk0=14: E=55
Для 2 реакции lnk0=4; E=25
8. Входим в подпрограмму Simulation wizard.
9. Нажимаем кнопку New для создания новой задачи моделирования.
Открывается окно создания модели с именем вновь созданной модели в списке моделей.
10. Нажимаем команду OK и открывается список реакций и констант
модели, которые можно редактировать.
11. Нажимаем команду Next, открывается окно задания интервала интегрирования и количества точек выдачи решения. Оставляем предложенные по умолчанию 100 минут и 21 точка.
12. Нажимаем клавишу Next, открывается окно задания температуры. По умолчанию предлагается температуры 400 К. Кликаем левой клавишей мышки по полю рисунка, открывается таблица задания температуры и задаем температуру в виде линейного изменения температуры в интервале от 300 К при нуле и 400 К при 100 мин.
13. Нажимаем клавиалшу Next, открывается окно задания начальных условий. Задаем начальную концентрацию исходного продукта А=10 кмоль/м3. Нажимаем команду solve.
14. Нажимаем команду Next и переходим на страницу сохранения результатов. Сохраняем результаты моделирования по команде Save как результаты моделирования и по команде Save as experiment как результаты наблюдения за реактором.
15. Параметры модели определяются из условия минимального рассогласования между результатами моделирования и экспериментальными данными:
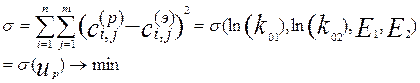 (1)
(1)
Процедура поиска минимума функции рассогласования осуществляется следующим образом:
1. Задаются некоторым начальным приближением искомых параметров up(0).
2. Вычисляется градиент функции рассогласования по искомым параметрам:
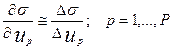
3. Далее изменяют искомые параметры в соответствии со следующим алгоритмом:
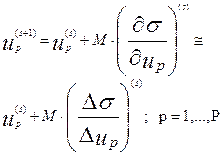
где s-номер шага поиска, М –коэффициент пропорциональности изменения параметра в направлении градиента минимизируемой функции. При градиентном методе параметры изменяются на каждом шаге поиска в направлении градиента, однако, этот метод требует большого объема вычислений, связанных с необходимостью вычисления градиента функции в каждой точке поиска. Для сокращения объема вычислений применяют обычно так называемый метод наискорейшего спуска.
При использовании этого метода после каждого шага по направлению к экстремуму, проверяется, удачным ли был этот шаг:
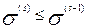
16. Входим в подпрограмму Estimation. Нажимаем команду New.Появляется окно со списком используемых моделей. Отмечаем мышкой созданную ранее модель и нажимаем клавишу OK. Появляется окно с предложеиием загрузки экспериментальных данных. Нажимаем команду Load Experiment. Открывается окно со списком экспериментальных данных. Отмечаем имя экспериментальных данных и нажимаем команду Load. Появляется окно с перечнем переменных, которые можно использовать для формирования функции рассогласования в соответствии с формулой (1) в пункте 15.
Отмечаем в списке выбранные переменные двойным щелчком левой кнопки мышки и нажимаем команду Next. Открывается окно выбора метода оптимизации и настройки точности вычисления. Принимаем предложения по умолчанию и попадаем в окно со списком экспериментальным данных с указанием настроек поиска. Нажимаем клавишу Next.
17. Попадаем в окно задания начального приближения. В качестве начального приближения задаем следующие значения:
Для 1 реакции lnk0=20, min=10, max=50: E=80, min=10, max=100
Для 2 реакции lnk0=2;min=1, max=6, E=15, min=5, max=20
Нажимаем кнопку Residuals, получаем величину 294,812. Далее нажимаем кнопку Next и далее нажимаем кнопку Visualization, просматриваем графики сопоставления экспериментальных и расчетных данных. Рассогласование довольно значительное. Сохраняем графики рассогласования при начальном приближении для последующего помещения в отчет, сохраняя их в промежуточной специально созданной папке.
18. После этого нажимаем кнопку Start и включается процедура поиска. Residuals становится равной 8.11×10-27. Нажимаем кнопку Accept и просматриваем графики сопоставления расчетных и экспериментальных данных. Затем нажимаем кнопку Next и просматриваем результаты статистического анализа. В первой строке написано: Model fits experimental data. Это означает, что модель адекватно описывает экспериментальные данные. Синтезируем отчет о проделанной работе, нажимая кнопку W.
В синтезированный отчет добавляем графики сопоставления экспериментальных и расчетных данных при начальных приближениях, и при найденных оптимальных значениях, а также значения Residuals.
19. Формулируются выводы по работе.
Методические указания к выполнению работы №2. Определение оптимального времени пребывания в проточном реакторе идеального перемешивания для последовательных реакций 1-го порядка для максимального выхода промежуточного продукта при 4-х различных температурах по найденной в предыдущей работе модели.
Порядок выполнения работы следующий:
1.Разделить заданный температурный диапазон 300 – 500 К на четыре равные промежутка.
2. По найденным значениям lnk0 и E вычислить значения констант скорости в четырех точках k1(Ti), k2(Ti).
3. Вычислить значения времени пребывания, обеспечивающие оптимальный выход целевого продукта:

4. Задавшись объемом реактора 1 м3 вычислить расход смеси, обеспечивающий оптимальной время пребывания:
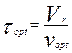
5. Войти в ReactOp и построить модель проточного реактора с заданными температурным режимом и с найденными ранее значениями кинетических параметров и начальной концентрацией реагента, равной 10 кмоль/м3.
6. Сохранить модель под новым именем.
7 Войти в Simulation и создать новую задачу с полученной моделью.
8 Решить задачу четыре раза, задавая определенные температуры и найденные оптимальные расходы, сохраняя каждый раз результаты под разными именами
9. Создать отчет по моделированию, вставив в один отчет результаты всех четырех решений. Выбрать из решений максимальную концентрацию целевого продукта Р и вычислить максимальную конверсию исходного вещества в целевой продукт:
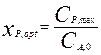
10. Построить график зависимости хP,opt от температуры в программном комплексе Excel
11. Определить оптимальную температуру, обеспечивающую максимальный выход целевого продукта.
Методические указания для выполнения работы №3 «Сопоставление выхода целевого продукта в проточном реакторе идеального перемешивания и идеального вытеснения при времени пребывания, равном оптимальному для реактора идеального перемешивания».
1. Cоздать модель процесса для аппарата идеального вытеснения в котором протекают последовательные реакции 1-го порядка. Использовать кинетические параметры, полученные в работе №1.
Для этого войти в ReactOp, далее в DEMO, выбрать реактор Plug flow reactor liquid (Закд) с температурным режимом Tgiven
2. Создать Задачу моделирования, войдя в Simulation и задав одну из температур и время пребывания из предыдущей задачи. Объем реактора задать равным 1 м3. Отношение длины реактора к диаметру задать равным 10.
3. Проделать моделирование при заданных условиях и сравнить результаты, с результатами, полученными в предыдущей задаче с использование модели реактора идеального перемешивания
4. Провести аналогичные расчеты для всех 4-х температур предыдущей задачи.
5. Вычислить оптимальную конверсию исходного продукта в целевой продукт
6. Построить графики зависимости степени конверсии в целевой продукт от температуры для реактора идеалного перемешивания и идеального вытеснения
7. Оформить отчет с выводами о характере влияния гидродинамического режима на результаты функционирования объекта.
