Определение параметров эмпирических формул

Исходные данные:

Исследуя зависимость между явлениями Х и У экспериментатор выявил с точностью до неизвестных параметров к и т вид этой зависимости в виде: .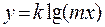

Для определения неизвестных параметров к и т был поставлен эксперимент, по результатам которого получены для десяти значений аргумента Х соответствующие значения функции У. Результаты эксперимента приведены в таблице:

Х	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0
У	-0,86	-0,14	0,27	0,57	0,74	0.94	1,07	1,25	1,35	1,47

Необходимо:

1. По методу наименьших квадратов вычислить наилучшие приближения к искомым значениям параметров к и т.

2. Вычислить СКП расчетных значений параметров к и т.

3. Вычислить СКП значений функции У, определяемых по значениям аргументов Х с использование полученного соотношения.

4. Построить график зависимости: 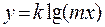. Нанести на этот график эмпирические точки.

Порядок выполнения:

1. По указанию преподавателя вносят изменения в исходные данные.

2. По двум парам значений Х и У , выбираемых по указанию преподавателя, составляют два уравнения с двумя неизвестными. В результате решения этих уравнений находят нулевые приближения k₀ и m₀ неизвестных параметров.

3. Вычисляют значения частных производных 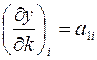и .

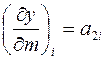
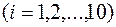4. По формуле 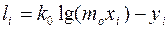вычисляют элементы столбца свободных членов.

5. Составляют два нормальных уравнения вида

.

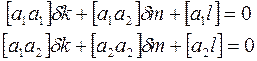6. Решают нормальные уравнения и находят поправки к нулевым приближениям неизвестных параметров, а затем неизвестные параметры в первом приближении по формулам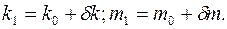

7. По новым вычисленным значениям параметров вновь вычисляют значения частных производных и свободных членов, заново составляют и решают нормальные уравнения и находят новые приближения искомых параметров.

8. Процесс приближений делается до тех пор, пока два соседних приближения не будут отличаться друг от друга на величины, меньшие 0, 001.Значения параметров в последнем приближении и будут являться искомыми.

9. По последним значения коэффициентов нормальных уравнений составляют и решают весовые уравнения.

10. Оценку точности выполняют по следующим формулам:

· СКП единичного веса - 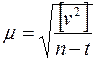, где 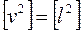, причем величины l берутся по последнему приближению.

· СКП величины к ;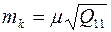

· СКП величины т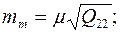

· СКР определения любого значения функции 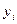по полученному уравнению .

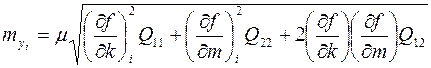Вычисления следует выполнить для всех десяти значений аргумента Х.

11. Строят график функции с определенными параметрами и наносят на него эмпирические точки.

Приложение 1

Таблица значений функции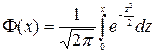
(таблица распределения функции Лапласа)

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0,00	0,0000	0,32	0,1255	0,64	0,2389	0,96	0,3315
0,01	0,0040	0,33	0,1293	0,65	0,2422	0,97	0,3340
0,02	0,0080	0,34	0,1331	0,66	0,2454	0,98	0,3365
0,03	0,0112	0,35	0,1368	0,67	0,2486	0,99	0,3389
0,04	0,0160	0,36	0,1406	0,68	0,2518	1,00	0,3413
0,05	0,0199	0,37	0,1443	0,69	0,2549	1,01	0,3438
0,06	0,0239	0,38	0,1480	0,70	0,2580	1,02	0,3461
0,07	0,0279	0,39	0,1517	0,71	0,2612	1,03	0,3485
0,08	0,0319	0,40	0,1554	0,72	0,2642	1,04	0,3508
0,09	0,0359	0,41	0,1591	0,73	0,2673	1,05	0,3531
0,10	0,0398	0,42	0,1628	0,74	0,2704	1,06	0,3553
0,11	0,0438	0,43	0,1664	0,75	0,2734	1,07	0,3577
0,12	0,0478	0,44	0,1700	0,76	0,2764	1,08	0,3599
0,13	0,0517	0,45	0,1736	0,77	0,2794	1,09	0,3621
0,14	0,0557	0,46	0,1772	0,78	0,2823	1,10	0,3643
0,15	0,0596	0,47	0,1808	0,79	0,2852	1,11	0,3665
0,16	0,0636	0,48	0,1844	0,80	0,2881	1,12	0,3686
0,17	0,0675	0,49	0,1879	0,81	0,2910	1,13	0,3708
0,18	0,0714	0,50	0,1915	0,82	0,2939	1,14	0,3729
0,19	0,0754	0,51	0,1950	0,83	0,2967	1,15	0,3749
0,20	0,0793	0,52	0,1985	0,84	0,2996	1,16	0,3770
0,21	0,0832	0,53	0,2019	0,85	0,3023	1,17	0,3790
0,22	0,0871	0,54	0,2054	0,86	0,3051	1,18	0,3810
0,23	0,0910	0,55	0,2088	0,87	0,3079	1,19	0,3830
0,24	0,0948	0,56	0,2123	0,88	0,3106	1,20	0,3849
0,25	0,0987	0,57	0,2157	0,89	0,3133	1,21	0,3869
0,26	0,1026	0,58	0,2190	0,90	0,3159	1,22	0,3888
0,27	0,1064	0,59	0,2224	0,91	0,3186	1,23	0,3907
0,28	0,1103	0,60	0,2258	0,92	0,3212	1,24	0,3925
0,29	0,1141	0,61	0,2291	0,93	0,3238	1,25	0,3944
0,30	0,1179	0,62	0,2324	0,94	0,3264	1,26	0,3962
0,31	0,1217	0,63	0,2357	0,95	0,3289	1,27	0,3980

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,28	0,3997	1,63	0,4485	1,98	0,4761	2,66	0,4961
1,29	0,4015	1,64	0,4495	1,99	0,4767	2,68	0,4963
1,30	0,4032	1,65	0,4505	2,00	0,4772	2,70	0,4965
1,31	0,4049	1,66	0,4515	2,02	0,4783	2,72	0,4967
1,32	0,4066	1,67	0,4525	2,04	0,4793	2,74	0,4969
1,33	0,4082	1,68	0,4535	2,06	0,4803	2,76	0,4971
1,34	0,4099	1,69	0,4545	2,08	0,4812	2,78	0,4973
1,35	0,4115	1,70	0,4554	2,10	0,4821	2,80	0,4974
1,36	0,4131	1,71	0,4564	2,12	0,4830	2,82	0,4976
1,37	0,4147	1,72	0,4573	2,14	0,4838	2,84	0,4977
1,38	0,4162	1,73	0,4582	2,16	0,4846	2,86	0,4979
1,39	0,4177	1,74	0,4591	2,18	0,4854	2,88	0,4980
1,40	0,4192	1,75	0,4599	2,20	0,4861	2,90	0,4981
1,41	0,4207	1,76	0,4608	2,22	0,4868	2,92	0,4982
1,42	0,4222	1,77	0,4616	2,24	0,4875	2,94	0,4984
1,43	0,4236	1,78	0,4625	2,26	0,4881	2,96	0,4985
1,44	0,4251	1,79	0,4633	2,28	0,4887	2,98	0,4986
1,45	0,4265	1,80	0,4641	2,30	0,4893	3,00	0,4986
1,46	0,4279	1,81	0,4649	2,32	0,4898	3,20	0,4993
1,47	0,4292	1,82	0,4656	2,34	0,4904	3,40	0,4997
1,48	0,4306	1,83	0,4664	2,36	0,4909	3,60	0,4998
1,49	0,4319	1,84	0,4671	2,38	0,4913	3,80	0,4999
1,50	0,4332	1,85	0,4678	2,40	0,4918	4,00	0,49997
1,51	0,4345	1,86	0,4686	2,42	0,4922	4,50	0,499997
1,52	0,4357	1,87	0,4693	2,44	0,4927	5,00	0,499999
1,53	0,4370	1,88	0,4700	2,46	0,4931
1,54	0,4382	1,89	0,4706	2,48	0,4934
1,55	0,4394	1,90	0,4713	2,50	0,4938
1,56	0,4406	1,91	0,4719	2,52	0,4941
1,57	0,4418	1,92	0,4726	2,54	0,4945
1,58	0,4430	1,93	0,4732	2,56	0,4948
1,59	0,4441	1,94	0,4738	2,58	0,4951
1,60	0,4452	1,95	0,4744	2,60	0,4953
1,61	0,4463	1,96	0,4750	2,62	0,4956
1,62	0,4474	1,97	0,4756	2,64	0,4959

Приложение 2

Критические точки распределения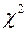

Число степеней свободы	Уровень значимости
0,01	0,025	0,05	0,95	0,975	0,99
	6,6	5,0	3,8	0,0039	0,00098	0,00016
	9,2	7,4	6,0	0,103	0,051	0,020
	11,3	9,4	7,8	0,352	0,216	0,115
	13,3	11,1	9,5	0,711	0,484	0,297
	15,1	12,8	11,1	1,15	0,831	0,554
	16,8	14,4	12,6	1,64	1,24	0,872
	18,5	16,0	14,1	2,17	1,69	1,24
	20,1	17,5	15,5	2,73	2,18	1,65
	21,7	19,0	16,9	3,33	2,70	2,09
	23,2	20,5	18,3	3,94	3,25	2,56
	24,7	21,9	19,7	4,57	3,82	3,05
	26,2	23,3	21,0	5,23	4,40	3,57
	27,7	24,7	22,4	5,89	5,01	4,11
	29,1	26,1	23,7	6,57	5,63	4,66
	30,6	27,5	25,0	7,26	6,26	5,23
	32,0	28,8	26,3	7,96	6,91	5,81
	33,4	30,2	27,6	8,67	7,56	6,41
	34,8	31,5	28,9	9,39	8,23	7,01
	36,2	32,9	30,1	10,1	8,91	7,63
	37,6	34,2	31,4	10,9	9,59	8,36
	44,3	40,6	37,7	14,6	13,1	11,5
	50,9	47,0	43,8	18,5	16,8	15,0
	57,3	53,2	49,8	22,5	20,6	18,5
	63,7	59,3	55,8	26,5	24,4	22,2
	70,0	65,4	61,7	30,6	28,4	25,9
	76,2	71,4	67,5	34,8	32,4	29,7
	82,3	77,4	73,3	39,0	36,4	33,6
	88,4	83,3	79,1	43,2	40,5	37,5
	100,4	95,0	90,5	51,7	58,8	45,4
	112,3	106,6	101,9	60,4	57,2	53,5
	124,1	118,1	113,1	69,9	65,6	61,8
	135,8	129,6	124,3	77,9	74,2	70,1

Приложение 3

Критические точки распределения Стьюдента

Число степеней свободы	Уровень значимости (двусторонняя критическая область)
0,1	0,05	0,02	0,01	0,002	0,001
	6,31	12,70	31,82	63,70	318,30	637,00
	2,92	4,30	6,97	9,92	22,33	312,60
	2,35	3,18	4,54	5,84	10,22	12,90
	2,13	2,78	3,75	4,60	7,17	8,61
	2,01	2,57	3,37	4,03	5,89	6,86
	1,94	2,45	3,14	3,71	5,21	5,96
	1,89	2,36	3,00	3,50	4,79	5,40
	1,86	2,31	2,90	3,36	4,50	5,04
	1,83	2,26	2,82	3,25	4,30	4,78
	1,81	2,23	2,76	3,17	4,14	4,59
	1,80	2,20	2,72	3,11	4,03	4,44
	1,78	2,18	2,68	3,05	3,93	4,32
	1,77	2,16	2,65	3,01	3,85	4,22
	1,76	2,14	2,62	2,98	3,79	4,14
	1,75	2,13	2,60	2,95	3,73	4,07
	1,75	2,12	2,58	2,92	3,69	4,01
	1,74	2,11	2,57	2,90	3,65	3,96
	1,73	2,10	2,55	2,88	3,61	3,92
	1,73	2,09	2,54	2,86	3,58	3,88
	1,73	2,09	2,53	2,85	3,55	3,85
	1,71	2,06	2,49	2,79	3,45	3.72
	1,70	2,04	2,46	2,75	3,39	3,65
	1,68	2,02	2,42	2,70	3,31	3,55
	1,67	2,00	2,39	2,66	3,23	3,46
	1,67	1,99	2,38	2,64	3,21	3,43
	1,66	1,98	2,37	2,63	3,19	3,40
	1,66	1,98	2,36	2,62	3,17	3,37
∞	1,64	1,96	2,33	2,58	3,09	3,29
	0,05	0,025	0,01	0,005	0,001	0,0005
Уровень значимости (односторонняя критическая область)