Проверка теоремы Гюйгенса - Штейнера методом вращательных колебаний
Цель лабораторной работы
Изучение возможности проверки теоремы Штейнера методом вращательных колебаний.
Задачи лабораторной работы
Используя результаты измерений момента инерции свободного стола и периода его колебаний методом вращательных колебаний, провести экспериментальную и теоретическую проверку теоремы Гюйгенса -Штейнера.
Экспериментальное оборудование, приборы и
Принадлежности
 |
Рис.1
Лабораторная установка (рис.1) включает колебательную систему 1, вращающуюся в горизонтальной плоскости, и устройство 2 для измерения жесткости используемых пружин.
К приборами
Принадлежностям относятся
оптический датчик 3, с помощью которого измеряется период колебаний системы, компьютер с необходимым программным обеспечением и концентратор для подключения датчика к компьютеру.
Рис.2
Колебательная система (рис.2) состоит из закрепленного на вертикальной оси шкива 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки. К шкиву жестко прикреплен металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6. Вращательные колебания регистрируются оптическим датчиком 7 в форме импульсов при перекрытии оптической оси датчика язычком 8, жестко скрепленным со шкивом колебательной системы.
Теоретическая часть
Найдем связь между моментом инерции Jподвижной части колебательной системы и периодом колебаний Т. В положении равновесия силы упругости пружин, а, следовательно, и силы натяжения нити с разных сторон от стола, равны. Обозначим эти силы F0. Для выведения шкива из положения равновесия повернем его на угол φ. Тогда натяжение одной пружины увеличится, а другой уменьшится на φd/2, где d — радиус шкива. По закону Гука силы упругости изменятся на kdφ/2, здесь k- коэффициент жесткости одной пружины. На шкив будет действовать возвращающий момент сил:
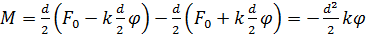(1)
Согласно основному уравнению вращательного движения
Jε= М. (2)
Подставляя (1) в (2)и учитывая, что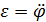 
, получаем
дифференциальное уравнение для φ:
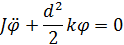
Из теории дифференциальных уравнений следует, что его решение имеет вид:
φ(t)= φ0cos(ωt + α). Здесь φ0 и α- константы, определяемые начальными условиями, а
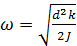(3)
- частота колебаний. Из формулы (3) видим, что момент инерции обратно пропорционален квадрату частоты:
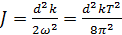(4)
Здесь учтено, что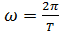 
Следовательно, моменты инерции
подвижной части колебательной системы относятся как квадраты частот их колебаний. Окончательно получаем, что отношение моментов инерции подвижной части колебательной системы
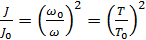(5)
Здесь нулевым индексом отмечены параметры системы, выбранной в качестве эталонной.
За эталонную примем такую подвижную систему, у которой грузы (рис.3) располагаются соосно на оси шкива - в его центральном отверстии, один над другим (в позиции "0-0").
Жесткость упругой связи к, входящую в выражение (4), можно определить по величине растяжения пружин X под действием весовой нагрузки:
G = kX, (6)
Откуда
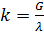(7)
Рис.3
Для определения момента инерции эталонной системы Jo применим формулу (4):
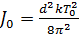(8)
Сформулируем теорему Гюйгенса- Штейнера:
Момент инерции тела относительно произвольной оси равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между этими осями.
Следовательно, момент инерции подвижной системы, у которой два одинаковых груза фиксированной массы т располагаются симметрично на расстоянии гот оси шкива (рис.3, позиции "1-1", "2-2", "3-3", или "4-4") определяется выражением
J = J0 + 2mr2. (9)
Разместим на одинаковых расстояниях г от оси шкива 2 тела фиксированной массы т. После измерения периода колебаний Т производится вычисление момента инерции по формуле 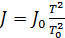(10)
(10)
где Т. и J- - период колебаний и момент инерции эталонной системы. Для проверки теоремы Штейнера по формуле (9) производится расчет момента инерции J- (его теоретическое значение) и сравнивается со значением момента инерции Jэ(10), оцененного экспериментально.