Описание метода и экспериментальной установки
для определения ускорения свободного падения
Метод основан на исследовании движения двух грузов, связанных нитью, перекинутой через неподвижный блок (рис. 1).
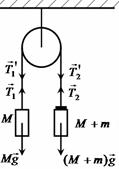Грузы имеют одинаковые массы 
, величина которых значительно превышает массу нити. Если на один из грузов положить дополнительный груз (перегрузок) массы 
, то они начинают двигаться прямолинейно и равноускоренно с некоторым ускорением 
, а блок начинает вращаться с угловым ускорением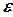 
.
Применяя второй закон Ньютона, запишем уравнения движения грузов в проекциях на оси:
а) для груза без перегрузка:
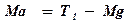, (1)
б) для груза с перегрузком
|
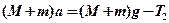, (2) где – ускорение движения грузов; 
и 
– силы натяжения нити (см. рис. 1); 
– ускорение свободного падения.
Уравнение вращения блока (так как по 3-му закону Ньютона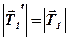 
и
):
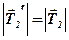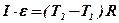, (3)
где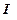 
– момент инерции блока; 
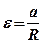– угловое ускорение блока; 
– радиус блока.
Решая систему уравнений (1) – (3), получим формулу для определения ускорения свободного падения в виде:
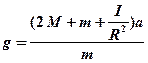. (4)
Из выражения (4) следует, что для определения ускорения свободного падения необходимо знать массы грузов и перегрузка , момент инерции блока 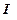и ускорение движения грузов 
.
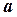Ускорение движения грузов определяется из формулы пути при равноускоренном движении:
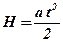, откуда 
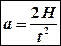, (5)
где 
– время, в течение которого грузы перемещаются на величину 
.
Подставив в формулу (4) выражение ускорения (5), получим:
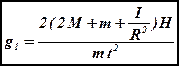– (6)
ускорение свободного падения, рассчитанное с учетом момента инерции блока.
Силы натяжения нити и имеют различные значения и могут быть определены из уравнений (1) и (2)
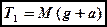, (7)
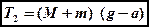. (8)
Если момент инерции блока настолько мал, что величиной 
можно пренебречь по сравнению с массой грузов , то выражение (6) получает вид:
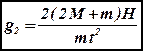- (9)
ускорение свободного падения, рассчитанное без учета момента инерции блока.
Силы натяжения нити при условии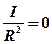 
имеют одинаковые значения 
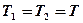. Определить силу натяжения можно из формул (7) либо (8).
Общий вид машины Атвуда показан на рис. 2.
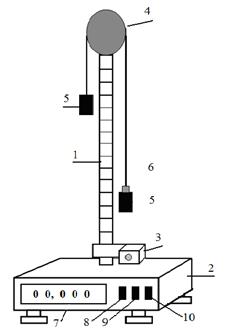
Рис. 2
Конструкция машины была предложена Д. Атвудом и названа в его честь. Машина представляет собой настольный прибор с вертикальной стойкой 1, на которой крепятся все основные элементы машины Атвуда, и основание 2. На вертикальной стойке 1 расположены два кронштейна: нижний 3 и верхний 4. На верхнем кронштейне 4 крепится блок с узлом подшипников качения, через блок перекинута нить с грузами 5 одинаковой массы. Перегрузок 6 кладут на правый груз 5. На верхнем кронштейне находится электромагнит, который с помощью фрикциона при подаче на него напряжения, удерживает систему с грузами в неподвижном состоянии. На нижнем кронштейне 3 крепится фотодатчик, который выдает электрический сигнал окончания счета времени равноускоренного движения грузов. Нижний кронштейн 3 представляет собой площадку с резиновым амортизатором, о который ударяется груз при его остановке. Нижний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке по всей ее свободной длине. На вертикальной стойке 1 укреплена миллиметровая линейка, по которой определяют начальное и конечное положения грузов, а следовательно, и пройденный путь. Начальное положение определяют визуально по нижнему срезу грузов, конечное положение – по индексу нижнего кронштейна. Секундомер 7 выполнен самостоятельным прибором и соединен кабелем с датчиком (фотоэлектрическим). На установке кнопка 8 – "сброс времени", кнопка 9 – "пуск", кнопка 10 – "сеть"
Порядок выполнения работы
Задание 1. Определение ускорения свободного падения с учетом момента инерции блока.
1. Перекинуть нить с двумя грузам через блок и при необходимости отрегулировать положение основания таким образом, чтобы груз с перегрузком проходил по середине рабочего окна фотодатчика.
2. Включить в сеть шнур питания секундомера.
3. Привести подвижную систему (грузы на нити) в исходное положение, т.е. установить правый груз в верхнее положение.
4. Нажать на кнопку "Сеть" секундомера, при этом сработает электромагнит и блок потеряет возможность вращаться.
5. Положить на правый груз перегрузок известной массы .
6. Определить пройденный путь правого груза по шкале как расстояние от верхнего до нижнего положений и занести в табл. 3.
7. Нажать на кнопку "Пуск" секундомера и определить время, в течение которого груз проходит расстояние . Опыт повторить не менее 5 раз. Результаты занести в табл. 1.
8. Произвести статистическую обработку времени и заполнить табл. 1 и 2.
9. Заполнить табл. 3 (масса грузов , перегрузка и указаны на установке).
10. По формуле (5) по среднему значению времени 
рассчитать ускорение движения грузов. Занести в табл. 3.
11. По формуле (6) по среднему значению времени определить ускорение свободного падения 
с учетом момента инерции блока. Занести в табл. 3.
12. Относительную и абсолютную погрешности при определении ускорения свободного падения найти по формулам:
,
.
13. По формулам (7) и (8) определить силы натяжения нити. Результаты записать в табл. 3.
14. Относительные и абсолютные погрешности при определении сил натяжения найти по формулам:
,
,
,
.
Результаты записать в табл. 3.
Задание 2. Определение ускорения свободного падения без учета момента инерции блока.
1. Используя данные табл. 1 и 3, по формуле (9) по среднему значению времени найти ускорение свободного падения 
, занести в табл. 3.
2. Относительную и абсолютную погрешности при определении ускорения свободного падения найти по формулам:
,
.
3. Сравнить результаты, полученные по формулам (6) и (9), рассчитать погрешность по формулам:
, 
,
где 
; 
– ускорение свободного падения, вычисленное по формуле (6); 
– ускорение свободного падения, вычисленное по формуле (9).
4. Сделать вывод.
Таблица 1
 | ||||||||
 ,  | ||||||||
| Dt, | ||||||||
 ,  |
Таблица 2
 |  |  |  |  |  |  |
| | – | – | | | | % |
Таблица 3
 | | | | | | | | | |
 |  | | |  |  | | | | |
  | |||||||||
 | |||||||||
 |
Контрольные вопросы
1. Что называется свободным падением тела?
2. От каких факторов зависит ускорение свободного падения?
3. Сформулировать законы Ньютона.
4. Записать закон всемирного тяготения.
5. Записать основной закон динамики вращательного движения.
6. Что называется моментом инерции материальной точки, твердого тела?
7. Что характеризует момент инерции и от каких факторов он зависит.
8. Теорема Штейнера.
9. Найти момент инерции однородного стержня массой 
и длиной 
относительно оси, проходящей на расстоянии 
от его конца.
Лабораторная работа №106