Интерференция в плоскопараллельной пластине

Общие методические указания

При решении и оформлении задач необходимо соблюдать следующие требования:

1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины.

2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график.

3. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Произвести вычисления по расчетной формуле с соблюдением правил приближенных вычислений.

Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.

ИНТЕРФЕРЕНЦИЯ СВЕТА

Основные формулы и законы

• Скорость света и длина волны в среде

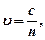
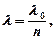
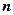где – скорость света в вакууме; – абсолютный показатель преломления среды, который показывает, во сколько раз скорость света в среде меньше, чем в вакууме; 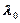– длина волны в вакууме.

• Оптическая длина пути световой волны

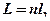
где 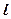– геометрическая длина пути световой волны в среде с показателем преломления .

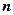• Оптическая разность хода двух световых волн

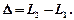
• Зависимость разности фаз 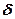от оптической разности хода 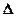световых волн:

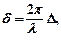
где 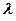– длина световой волны.

• Условие интерференционных максимумов

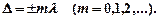
• Условие интерференционных минимумов

· Координаты максимумов и минимумов интенсивности в опыте Юнга

; ,

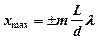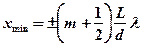где 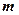= 0, 1, 2… – номер интерференционной полосы; 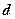– расстояние между двумя когерентными источниками, находящимися на расстоянии 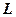от экрана .

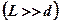• Ширина интерференционной полосы

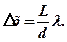
· Оптическая разность хода при интерференции в тонких плёнках в проходящем свете:

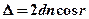или ,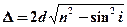

в отражённом свете:

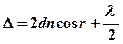или ,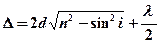

где 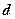– толщина пленки; 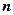– ее показательпреломления; 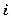– угол падения; 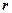– угол преломления.

• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем свете)

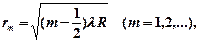
где 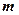– номер кольца; 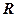– радиус кривизны линзы.

• Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем свете)

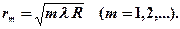
• В случае «просветления оптики» интерферирующие лучи в отраженном свете гасят друг друга при условии

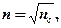
где 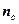– показатель преломления стекла; 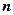– показатель преломления пленки.

Задания

Опыт Юнга

1.1. Расстояние от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной 1 см укладывается 10 темных интерференционных полос. Длина волны равна 0,7 мкм. [0,63 мм].

1.2. Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный (l= 750 нм), б) зеленый (l= 500 нм)? [а) усиление; б) ослабление].

1.3. Разность хода двух интерферирующих лучей монохро­мати­ческого света 0,3l. Определить разность фаз колебаний. [108°].

1.4.Расстояние между двумя щелями в опыте Юнга равно 1 мм, расстояние от щелей до экрана 3 м, расстояние между максимумами яркости смежных интерференционных полос на экране 1,5 мм. Определить длину волны источника монохроматического света. [500 нм].

1.5.В опыте Юнга расстояние между щелями равно 1 мм, а расстояние от щелей до экрана равно 3 м. Определить: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны 0,5 мкм. [1) ±1,5 мм; 2) ±5,25 мм].

1.6.Расстояние между двумя щелями в опыте Юнга равно 0,5 мм. Длина волны света равна 0,6 мкм. Определить расстояние от щелей до экрана, если ширина интерференционных полос равна 1,2 мм. [1 м].

1.7.Во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм). [1,75].

1.8.Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (l=0,5 мкм) заменить красным (l=0,65 мкм)? [В 1,3 раза].

1.9.В опыте Юнга отверстия освещались монохроматическим светом длиной волны 600 нм, расстояние между отверстиями 1 мм и расстояние от отверстий до экрана 3 м. Найти положение трех первых полос. [1,8 мм; 3,6 мм; 5,4 мм].

1.10.В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света равно 0,5 мм, расстояние от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определить длину волны света. [0,6мкм].

1.11.Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n=1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны света равна 0,5 мкм. Определить толщину пластины [5 мкм].

1.12.В опыте Юнга расстояние от щелей до экрана равно 3 м. Определить угловое расстояние между светлыми соседними полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на 4,5 мм. [5·10ˉ⁴ рад].

Интерференция в клине

1.26.На стеклянный клин (n=1,5) с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны 0,698 мкм. Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм. [ ].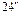

1.27.На тонкий стеклянный клин (n=1,5) нормально падает монохроматический свет. Угол клина равен 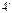. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм. [698 нм].

1.28.На стеклянный клин (n=1,5) падает нормально пучок света с длиной волны 0,582 мкм. Угол клина равен 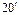. Какое число темных интерференционных полос приходится на единицу длины клина? [5 полос на 1 см].

1.29.Между двумя плоскопараллельными стеклянными пластинками (n=1,5) положили очень тонкую проволочку. Проволочка находится на расстоянии 75 мм от линии соприкосновения пластинок и ей параллельна. В отраженном свете с длиной волны 0,5 мкм на верхней пластинке видны интерференционные полосы. Определить толщину проволочки, если на протяжении 30 мм насчитывается 16 светлых полос. [10 мкм].

1.30.Между двумя плоскопараллельными стеклянными пластинками (n=1,5) на расстоянии 10 см от границы их соприкосновения находится проволока диаметром 0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим светом с длиной волны 0,6 мкм. Определить ширину интерференционных полос, наблюдаемых в отраженном свете. [3 мм].

1.31.Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами равно 0,4 мм. Определить расстояние между интерференционными полосами, если пространство между пластинами, образующими клин, заполнить прозрачной жидкостью с показателем преломления n=1,33. [0,3 мм].

Кольца Ньютона

1.32.Радиус второго темного кольца Ньютона в отраженном свете равен 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается светом с длиной волны 0,64 мкм. [125 мм].

1.33.Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 0,82 мм. Радиус кривизны линзы равен 0,5 м. [1,34].

1.34.На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны 500 нм. Найти радиус кривизны линзы, если радиус четвертого темного кольца Ньютона в отраженном свете равен 2 мм. [2 м].

1.35.Плосковыпуклая стеклянная линза с радиусом кривизны 0,5м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете равен 1,1 мм. Определить длину световой волны. [0,484 мкм].

1.36.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается первое светлое кольцо. [0,15 мкм].

1.37.Расстояние между вторым и первым тёмными кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние между десятым и девятым темными кольцами. [0,39 мм].

1.38.Диаметр второго светлого кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 1,2 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта. [0.4м].

1.39.Плосковыпуклая линза с радиусом кривизны 0,3 м выпуклой стороной лежит на стеклянной пластинке. Радиус четвертого темного кольца Ньютона в проходящем свете равен 0,7 мм. Определить длину световой волны. [0,47 мкм].

1.40.Плосковыпуклая линза с радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм. [0,5 мкм].

1.41.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 550 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается четвертое темное кольцо. [1,1 мкм].

1.42.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы равен 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца равен 1,8 мм. [1,48].

1.43.Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в проходящем свете с длиной волны 0,6 мкм равен 0,9 мм. Определить радиус кривизны линзы. [0,45 м].

1.44.Плосковыпуклая линза с радиусом сферической поверхности 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света. [0,2 мкм].

1.45.Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости. [1,46].

1.46.Найти радиус центрального темного пятна колец Ньютона, если между линзой и пластинкой налит бензол (n=1,5). Радиус кривизны линзы равен 1 м. Показатели преломления линзы и пластинки одинаковы. Наблюдение ведется в отраженном свете с длиной волны 589 нм. [0,63 мм].

Основные формулы и законы

· Радиус внешней границы 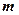- й зоны Френеля для сферической волны

,

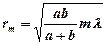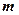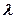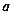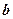где – номер зоны Френеля; – длина волны; и – расстояния от волновой поверхности соответственно до точечного источника и до экрана, на котором дифракционная картина наблюдается.

· Радиус внешней границы 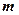- йзоны Френеля для плоской волны

,

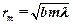где 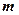– номер зоны Френеля; 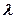– длина волны; 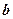– расстояние от диафрагмы с круглым отверстием до экрана, на котором дифракционная картина наблюдается.

· Условия дифракционных максимумов и минимумов от одной щели, на которую свет падает нормально:

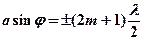– условие максимума

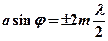– условие минимума

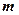( = 1, 2, 3, ...),

где 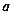– ширина щели; 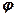– угол дифракции; 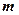– поря­док спектра; 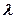– длина волны.

· Условия главных максимумов и минимумов, а также дополнительных минимумов дифракционной решетки, на которую свет падает нормально:

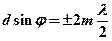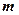( = 0, 1, 2,...) – условие максимума

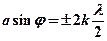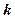– ( = 1, 2, 3...) – условие минимума

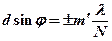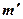( = 1, 2, 3,...,кроме 0, N, 2N,...) – условие добавочных минимумов, где 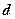– период (постоянная) дифракционной решетки; 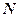– число штрихов решетки.

· Период дифракционной решетки

,

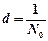где 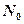– число щелей, приходящихся на единицу длины решетки.

· Условие дифракционных максимумов от пространст­венной решетки (формула Вульфа – Брэггов)

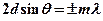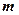( = 1, 2, 3, ...),

где 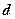– расстояние между атомными плоскостями крис­талла; 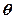– угол скольжения.

· Угловая дисперсия дифракционной решетки

.

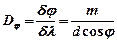· Разрешающая способность дифракционной решетки

,

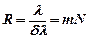где 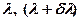– длины волн двух соседних спектраль­ных линий, разрешаемых решеткой; 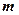– порядок спектра; 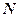– общее число штрихов решетки.

· Закон Малюса

,

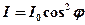где 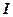– интенсивность плоскополяризованного света, прошедшего через анализатор; 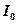– интенсивность плоскополяризованного света, падающего на анализатор; 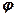– угол между главными плоскостями поляризатора и анализатора.

Если в анализаторе часть ( 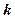) световой энергии поглощается и отражается (теряется на поглощение и отражение), то закон Малюса выглядит так:

.

· Закон Брюстера

,

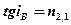где 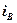– угол падения, при котором отраженный от диэлектрика луч является плоскополяризованным; 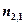– относительный показатель преломления второй среды относительно первой.

· Угол поворота плоскости поляризации:

– для оптически активных кристаллов и чистых жидкостей

;

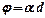– для оптически активных растворов

,

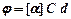где 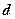– длина пути, пройденного светом в оптически активном веществе; 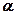- постоянная вращения; 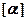– удельная постоянная вращения; 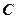– массовая концентрация оптически активного вещества в растворе.

Задания

Дифракция Френеля

2.1. Посередине между точечным источником монохроматического света (l=550 нм) и экраном находится диафрагма с круглым отверстием. Дифракционная картина наблюдается на экране, расположенном на расстоянии 5 м от источника. Определить радиус отверстия, при котором центр дифракционных колец, наблюдаемых на экране, будет наиболее темным. [1,17 мм].

2.2. Определить радиус третьей зоны Френеля, если расстояния от точечного источника света (l= 0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равны 1,5 м.[1,16 мм].

2.3. На диафрагму с круглым отверстием диаметром 5 мм падает нормально параллельный пучок света с длиной волны 0,6 мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля. [1) 5,21 м; 2) 3,47 м].

2.4. Определить радиус третьей зоны Френеля для случая плоской волны. Расстояние от источника до волновой поверхности и от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны 0,6 мкм. [1,64 мм].

2.5. Определить радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм. [2,83 мм].

2.6. Определить радиус первой зоны Френеля, если расстояния от точечного источника света (l = 0,5 мкм) до зонной пластинки и от пластинки до места наблюдения 1 м. [0,5 мм].

2.7. На зонную пластинку падает плоская монохро­матическая волна (l = 0,5 мкм). Определить радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения 1 м. [707 мкм].

2.8. Дифракция наблюдается на расстоянии 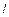от точечного источника монохроматического света (l = 0,5 мкм). Посередине между источником света и экраном находится непрозрачный диск диаметром 5 мм. Определить расстояние 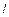, если диск закрывает только центральную зону Френеля. [50 м].

Поляризация света

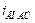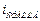2.45.1. Определить угол полной поляризации отраженного света для воды (n = 1,33), стекла (n =1,6) и алмаза (n = 2,42); 2. Как поляризован падающий луч, если в этом слу­чае отраженные лучи отсутствуют? [1) =53°, =58°, 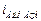=67°30¢; 2) плоско поляризован].

2.46. Угол преломления луча в жидкости 35°. Определить показатель преломления жидкости, если известно, что отраженный луч максимально поляризован. [1,4].

2.47. Свет падает под углом полной поляризации на границу раздела двух сред. Какой угол образуют между собой отраженный и преломленный лучи? [90°].

2.48. Предельный угол полного внутреннего отражения для некоторого вещества равен 60°. Чему равен для этого вещества угол полной поляризации? Какова скорость света в этом веществе? [49°6¢; 2,6×10⁸ м/с].

2.49. Пучок естественного света падает на стекло с показателем преломления 1,73. Определить, при каком угле преломления отраженный от стекла пучок света будет полностью поляризован. [30°].

2.50.Два николя расположены так, что угол между их главными плоскостями составляет 60°. 1. Во сколько раз уменьшится интенсивность естественного света при прохождении его через один николь? 2. Во сколько раз уменьшится интенсивность света при прохождении через оба николя? При прохождении каждого из николей потери на отражение и поглощение составляют 5%. [1) 2,1; 2) 9,1].

2.51. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через эти призмы, уменьшилась в 4 раза? Поглощением света пренебречь. [45°].

2.52. Главные плоскости двух призм Николя, поставленных на пути луча, образуют между собой угол 60°. Как изменится интенсивность света, прошедшего через эти призмы, если угол между их плоскостями поляризации станет равным 30°? [Увеличится в 3 раза].

2.53. Во сколько раз ослабляется естественный свет, проходя через два николя, главные плоскости которых составляют угол 30°, если в каждом из николей на отражение и поглощение теряется 10% падающего на него светового потока? [3,3].

2.54. Между двумя скрещенными поляроидами размещается тре­тий поляроид так, что его главная плоскость составляет угол 45° с главной плоскостью первого поляроида. Как изменится интенсивность естественного света, проходящего через такое уст­ройство? Поглощением света в поляроидах пренебречь. [Уменьшится в 8 раз].

2.55.Пучок естественного света падает на систему из четырех николей, главная плоскость каждого из которых повернута на угол 60° относительно главной плоскости предыдущего николя. Во сколько раз уменьшится интенсивность света, проходящего через эту си­стему? Поглощением света пренебречь. [В 128 раз].

2.56. Угол между главными плоскостями поляриза­тора и анализатора составляет 30°. Определить измене­ние интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°. [Уменьшится в 1,5 раза].

2.57.Интенсивность естественного света, прошед­шего через два николя, уменьшилась в 8 раз. Пренебрегая поглощением света, определить угол между главными плоскостями николей. [60°].

2.58. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями 60°, а в каждом из николей теряется 8% интенсив­ности падающего на него света. [В 9,45 раза].

2.59. Определить, во сколько раз уменьшится ин­тенсивность естественного света, прошедшего через два николя, главные плоскости которых образуют угол в 60°, если каждый из николей как поглощает, так и от­ражает 5% падающего на них света. [В 9,88 раза].

2.60. Естественный свет проходит через поляризатор и анализатор, угол между главными плоскостями которых равен j. Поляризатор и анализатор как погло­щают, так и отражают 10% падающего на них света. Определить угол, если интенсивность света, вышедшего из анализатора, равна 12% интенсивности света, падающего на поляризатор. [52°14'].

2.61. Узкий параллельный пучок рентгеновского излучения с длиной волны l = 245 нм падает на естественную грань монокристалла каменной соли. Определить расстояние между атомными плоскостями монокристалла, если дифракционный максимум второго порядка наблюдается при падении излучения к поверхности монокристалла под углом скольжения 61°. [0,28 пм].

2.62. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстояниеммежду его атомными плоскостями 0,3 нм. Определить длину волны рентгеновского излуче­ния, если под углом 30° к плоскости грани наблюдается дифракционный максимум первого порядка. [300 пм].

2.63. Кварцевая пластинка освещена монохроматическим светом определенной длины волны. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации j = 180°. Удельная постоянная вращения в кварце для данной длины волны [a] = 0,52 рад/мм. [6,04 мм].

2.64. Раствор глюкозы с массовой концентрацией 0,21 г/см³, находящийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через раствор, на угол 24°. Определить массовую концентрацию глюкозы в другом растворе в трубке такой же длины, если он поворачивает плоскость поляризации на угол 18°. [157 кг/м³].

2.65. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации света с длиной волны l=500 нм равен 48°. Постоянная вращения кварца для этой длины волны a= 30°/мм. [1,6 мм].

2.66. Определить удельное вращение раствора сахара, концентрация которого 0,33 г/см³, если при прохождении монохроматического света через трубку с раствором угол поворота плоскости поляризации 22°. Длина трубки 10 см. [6,67°×см²/г].

3. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ

Основные формулы и законы

· Поток энергии 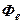, т.е. энергия, излучаемая (или поглощаемая) телом за единицу времени:

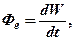
где 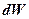– энергия, излучаемая (или поглощаемая) телом во всем диапазоне частот (длин волн) за время .

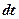· Энергетическая светимость тела:

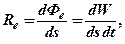
где 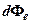– поток излучения с участка поверхности тела площадью .

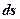· Закон Стефана-Больцмана

,

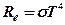где 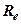– энергетическая светимость (излучательность) чёрного тела; 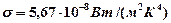– постоянная Стефана-Больцмана; 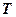– абсолютная температура.

· Энергетическая светимость серого тела

,

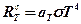где 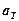– поглощательная способность серого тела.

· Спектральная плотность энергетической светимости

.

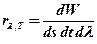· Связь энергетической светимости и спектральной плотности энергетической светимости чёрного тела

.

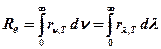· Закон смещения Вина

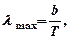
где 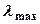– длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости чёрного тела; 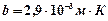– постоянная Вина.

· Зависимость максимальной спектральной плотности энергетической светимости чёрного тела от температуры

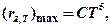
где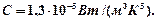

· Формула Рэлея-Джинса для спектральной плотности энергетической светимости чёрного тела

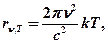
где – постоянная Больцмана;

– скорость света в вакууме; 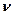– частота излучения.

· Энергия кванта света (фотона)

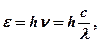
где 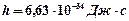- постоянная Планка.

· Импульс и масса фотона

, .

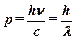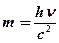· Формула Эйнштейна для внешнего фотоэффекта

,

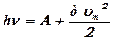где 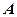– работа выхода электрона из металла; 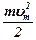– максимальная кинетическая энергия фотоэлектрона, 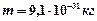– масса электрона.

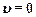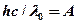Если , то или , где 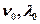– «красная граница» фотоэффекта, т.е. минимальная частота или максимальная длина волны, при которой возможен фотоэффект.

· Связь между максимальной кинетической энергией электрона и задерживающим напряжением

,

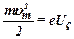где 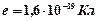– заряд электрона.

· Давление света при нормальном падении на поверхность

,

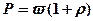где 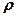– коэффициент отражения (для зеркальной поверхности 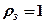, для чёрной поверхности 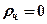); 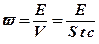– объёмная плотность энергии излучения; 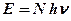– энергия всех фотонов; 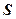– площадь поверхности, на которую падает свет; 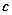– скорость света в вакууме; 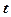– время воздействия света; 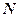– число фотонов; 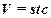- объем.

· Изменение длины волны рентгеновского излучения при комптоновском рассеянии

,

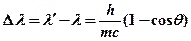где 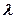и 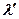– длина волны падающего и рассеянного излучения соответственно, 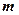– масса электрона, 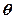– угол рассеяния.

Задания

Законы теплового излучения

3.1.Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны 0,48 мкм. Считая, что Солнце излучает как чёрное тело, определить температуру его поверхности и мощность, излучаемую его поверхностью. [6,04 кК; 4,58·10²⁶ Вт].

3.2.Определить количество теплоты, теряемой 50 см² поверхности расплавленной платины за 1 мин, если поглощательная способность платины 0,8. Температура плавления платины равна 1770^оС. [237 кДж].

3.3.Определить, во сколько раз необходимо уменьшить темпера­туру чёрного тела, чтобы его энергетическая светимость ослабилась в 16 раз. [В 2 раза].

3.4.Энергетическая светимость чёрного тела равна 10 кВт/м². Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела. [4,47 мкм].

3.5. Определить, как и во сколько раз изменится мощность излучения чёрного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с 720 нм до 400 нм. [Увеличится в 10,5 раз].

3.6.Чёрное тело находится при температуре 3000 К. При остывании тела длина волны, соответствующая максимуму энергетической светимости, изменилась на 8 мкм. Определить температуру, до которой тело охладилось. [323 К].

3.7.Чёрное тело нагрели от температуры 600 К до 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) на сколько уменьшилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости. [1) в 256 раз; 2) на 3,62 мкм].

3.8.В результате нагревания чёрного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилась с 2,7 мкм до 0,9 мкм. Определить, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. [1) в 81 раз; 2) в 243 раза].

3.9.Считая никель чёрным телом, определить мощность, необходимую для поддержания температуры расплавленного никеля 1453 ºС неизменной, если площадь его поверхности равна 0,5 см². Потерями энергии пренебречь. [25,2 Вт].

3.10. Металлическая поверхность площадью 15 см², нагретая до температуры 3000 К, излучает в одну минуту 100 кДж. Определить: 1) энергию, излучаемую этой поверхностью, считая её чёрной; 2) отношение энергетических светимостей этой поверхности и чёрного тела при данной температуре. [1) 413 кДж; 2) 0,242].

3.11.Принимая Солнце за чёрное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время вследствие излучения. [1) 5,8 кК; 2) 2,34·10²⁹Дж; 3) 2,6·10¹² кг].

3.12.Мощность излучения чёрного тела равна 34 кВт. Найти температуру этого тела, если его поверхность равна 0,6 м². [1000 К].

3.13.Температура вольфрамовой спирали в 25-ваттной электрической лампочке равна 2450 К. Отношение энергетической светимости лампочки и черного тела при данной температуре равно 0,3. Найти величину излучающей поверхности спирали. [4·10^-5м²].

3.14.Мощность излучения чёрного тела равна 10⁵ кВт. Найти величину излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности энергетической светимости, равна 700 нм. [14,4 см²].

3.15.Найти, какое количество энергии с одного квадратного сантиметра поверхности в одну секунду излучает чёрное тело, если известно, что максимум спектральной плотности энергетической светимости приходится на длину волны 4840 Å. [7350 Дж].

3.16.В каких областях спектра лежат длины волн, соответствующие максимуму спектральной плотности энергетической светимости, если в качестве источника света взять: 1) спираль электрической лампочки (Т=3000 К); 2) поверхность Солнца (Т=6000 К); 3) атомная бомба, имеющая в момент взрыва около 10 млн. градусов. Излучение считать близким к излучению чёрного тела. [1) 1 мкм; 2) 500 нм; 3) 2,9 Å].

3.17.На сколько процентов увеличится энергетическая светимость чёрного тела, если его температура увеличится на 1%? [На 4%].

Внешний фотоэффект

3.18.Красная граница фотоэффекта для цезия 6530 Å. Определить скорость фотоэлектронов при облучении цезия светом длиной волны 4000 Å. [6,5·10⁵ м/с].

3.19.Определить работу выхода электронов из натрия, если «красная граница» фотоэффекта равна 5000 Å. [2,49 эВ].

3.20.Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при задерживающем напряжении 3,7 В. [1,14 Мм/с].

3.21.«Красная граница» фот