Доказательство теоремы Гаусса
| dS |
| q |
| V |
| SV |
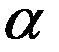³0. Элементарный поток через dS равен тогда 
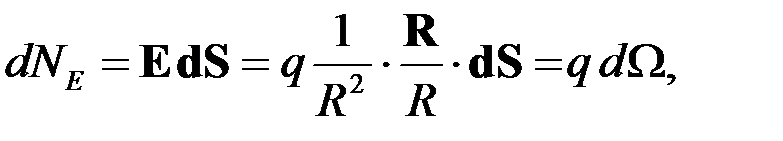(7)
где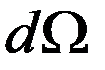 
–элементарный телесный угол, под которым видна площадка dS. При вычислении полного потока через SV мы суммируем все элементарные потоки, т. е. интегрируем по полному телесному углу, а поскольку в интеграле
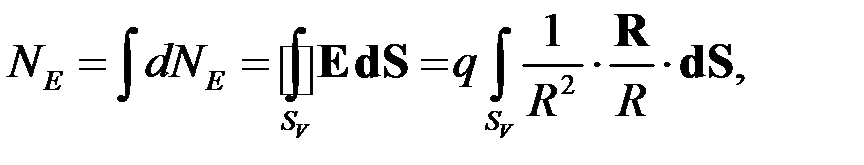(8)
они умножаются на постоянный множитель q, этот множитель вынесен за знак интеграла. Сам интеграл просто представляет собой полный телесный угол 4 
, и мы приходим к формуле (1)
Рассмотрим теперь систему точечных зарядов. Используя принцип суперпозиции, получим
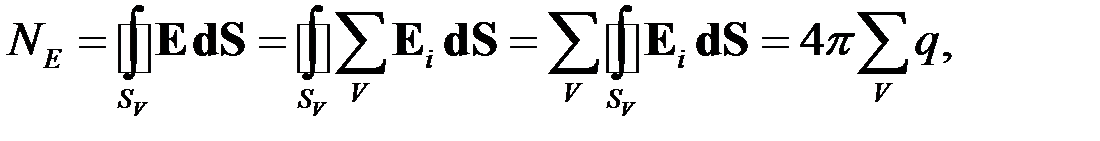(9)
где в соответствии с полученными соотношениями в сумму входят только заряды из объема V.
При непрерывном распределении зарядов каждый бесконечно малый объем можно рассматривать как точечный заряд, и к нему также применимы полученные соотношения . Это приводит нас к формуле (1), которую теперь можно считать доказанной. Ее называют электростатической теоремой Гаусса-Остроградского в интегральной форме.
Перепишем ее в СИ, умножив левую и правую часть на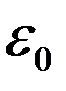 
:
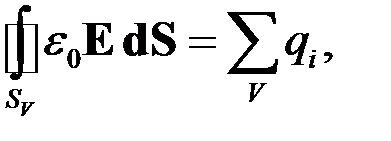(10)
или, короче,
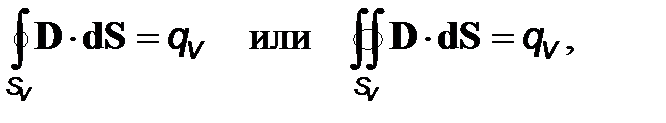(11)
где вектор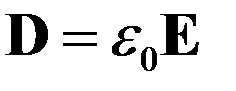 
называется электрическим смещением или электрической индукцией; справа–суммарный заряд, находящийся в объеме V. Таким образом, в СИ формулировка теоремы Гаусса-Остроградского предельно лаконична:
Поток электрической индукции из объема V равен суммарному заряду этого объема
Вектор Dэлектрического смещения вводится так просто только в вакууме. При изучении диэлектриков мы познакомимся с общим определением электрического смещения. Но и здесь и там он вводится для удобства, чтобы физические законы имели более простой вид.
Для областей пространства, в которых заряд непрерывно распределен по объему, электростатическая теорема Гаусса-Остроградского с помощью формулы Гаусса–Остроградского может быть приведена к иной форме:
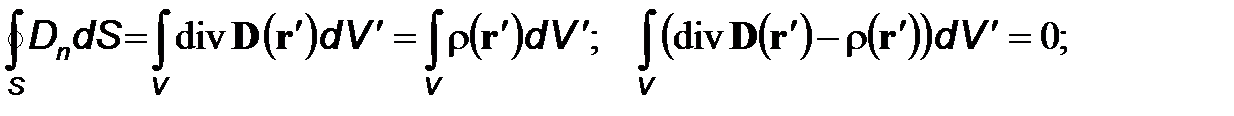
последний интеграл тождественно равен нулю для любой области пространства V, а это возможно, только если равно нулю подынтегральное выражение. Мы приходим, таким образом, к теореме Гаусса в дифференциальной форме
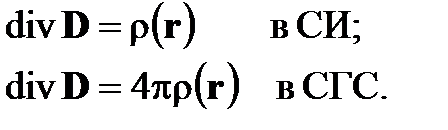(12)
Закон Био-Савара-Лапласа
Магнитная индукция движущегося со скоростью v заряда q, радиус-вектор которого в данный момент есть r¢, в точке с радиус-вектором r определяется соотношением вида
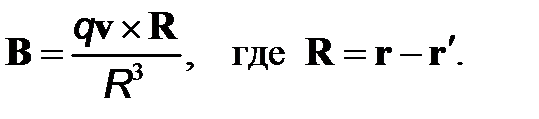(1)
В общем случае эта формула, должна содержать коэффициент пропорциональности, зависящий от системы единиц. Этот коэффициент пропорциональности принят равным единице в СГСМ. В СИ он равен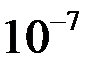 
Гн/м (точно) и записывается в виде 
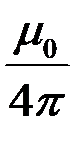. Коэффициент 
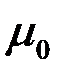называется магнитной постоянной. В СГС (симметричной системе Гаусса) коэффициент пропорциональности в формуле (1) равен 1/c.
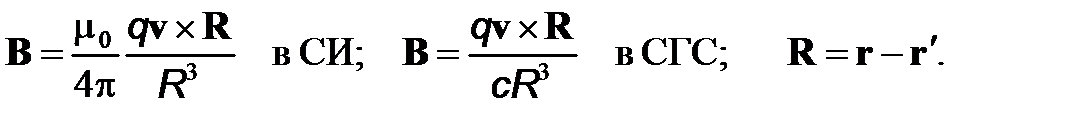(2)
Электрический ток представляет собой поток заряженных частиц, и потому также создает магнитное поле. Если средняя скорость заряженных частиц в малом объеме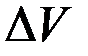 
равна u, а их счетная концентрация равна n, их суммарный заряд в указанном объеме равен 
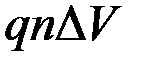. Ввиду малости 
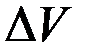считаем этот заряд точечным, поэтому магнитную индукцию этого заряда записываем в СГСМ по формуле (1):
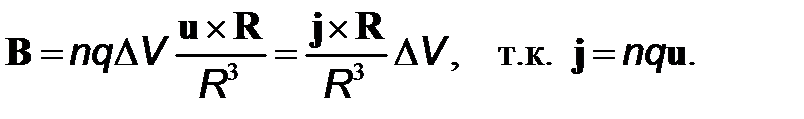
Бесконечно малый (физически) объем dV создает магнитную индукцию
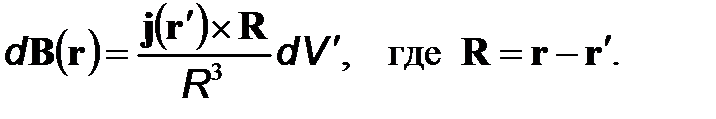
Конечный объем проводника, согласно принципу суперпозиции магнитных полей, создает поле (в СГСМ)
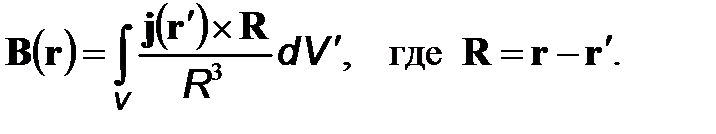(3)
Эта формула носит название закона Био–Савара–Лапласа для объемных токов.
Если ток течет по проводам, а магнитная индукция рассчитывается на расстояниях, больших по сравнению с поперечными размерами проводов, это выражение можно преобразовать к иному, более удобному для расчетов виду. Учтём, что
jdV=j∆Sdl=j(∆Sdl)=(j∆S)dl=Idl, (4)
где dl–длина отрезка провода, т. е. объема dV; dl–соответствующий этому отрезку провода вектор, ∆S–площадь поперечного сечения проводника, нормаль которой направлена в ту же сторону, куда и вектор dl. Здесь принято во внимание, что векторы j и dl параллельны и что j∆S представляет собой силу тока в проводнике в направлении, соответствующем направлению вектора dl. В результате приходим еще к одной формуле, выражающей закон Био–Савара–Лапласа, но уже для линейных токов. Для элемента тока бесконечно малой длины
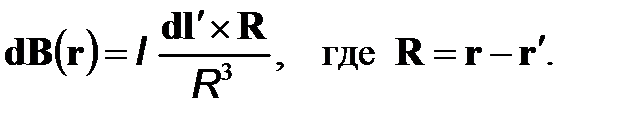(5)
Для провода конечной длины
.
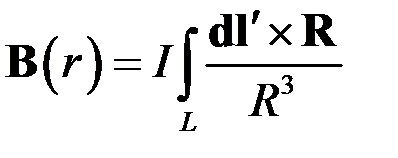