Основной закон электромагнитной индукции
Физических причин возникновения индукционного тока могут быть две, но результат один:
= 
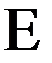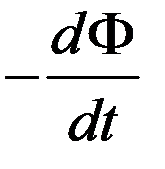
–основной закон электромагнитной индукции:
| ................................................. |
| - |
| - |
| B |
| v |
| F |
| Рис. 1 |
| + |
= 
.
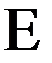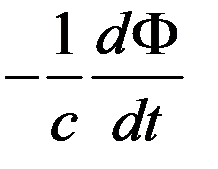Рассмотрим эти две причины.
1. Магнитное поле не меняется со временем.
Пусть в однородном магнитном поле с индукцией B в плоскости, перпендикулярной вектору B, поступательно движется со скоростью v прямолинейный металлический проводник длиной l в направлении, перпендикулярном проводнику (рис. 1). Действующая на свободные электроны проводника магнитная сила (в СИ) F=-ev×B, где e–элементарный заряд,станет смещать электроны вдоль проводника, в результате чего один торец (1), потеряв некоторое количество электронов, приобретёт положительный заряд, на другом (торце 2) окажется избыточное количество электронов, и он приобретёт отрицательный заряд. Порожденное этим зарядом электрическое поле будет противодействовать магнитной силе[1], и при
F=-e(E+v´B)=0, E=-v´B
электрическая и магнитная силы уравновесят друг друга. Подставляя последнюю формулу в выражение для разности потенциалов (интеграл от напряжённости электрического поля вдоль отрезка, соединяющего противолежащие точки торцевых поверхностей проводника), находим
| .................................................................................... |
| - |
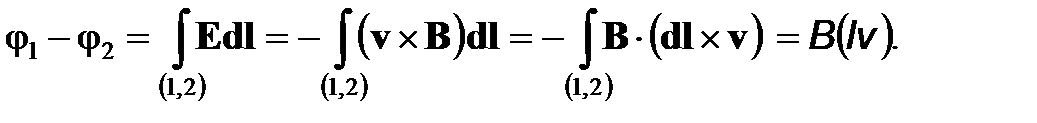
| G |
| B |
| v |
| F |
| Рис. 2 |
| + |
Пусть теперь этот проводник скользит по двум параллельным прямолинейным проводникам, присоединённым к гальванометру, как показано на рис. 2. Под действием разности потенциалов B(lv) между точками 1 и 2 через
гальванометр потечёт ток. Действующая в этом контуре в направлении по часовой стрелке ЭДС равна B(lv), и если суммарное сопротивление проводов контура и гальванометра равно R, то гальванометр покажет ток силой
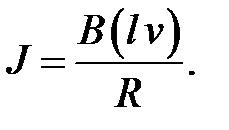
Легко увидеть, если ось X направить по вектору скорости проводника, то произведение
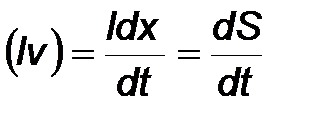
представляет собой приращение площади контура, по которому потечёт ток, за единицу времени, а
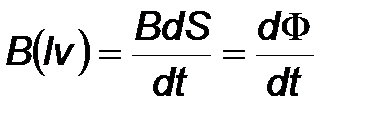
величину скорости изменения магнитного потока через площадь контура. Учитывая, что при выбранном направлении обхода контура векторы магнитной индукции и нормали к площади направлены в противоположные стороны, можем записать
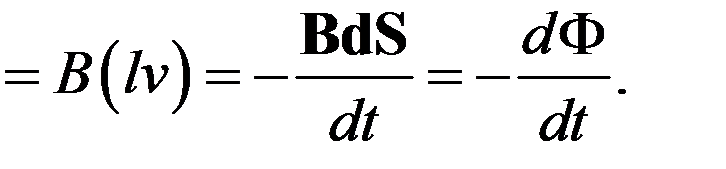
Трактовка Максвелла
.
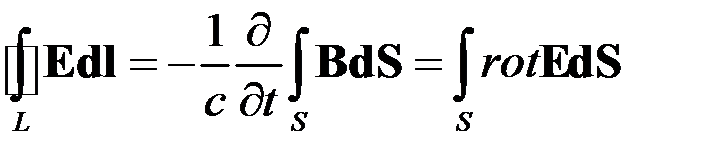Отсюда вытекает дифференциальная форма закона электромагнитной индукции
.
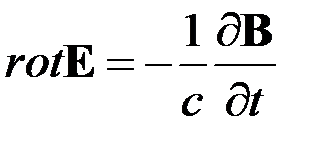Закон Кулона
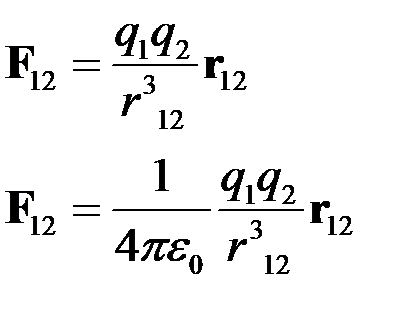
Здесь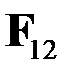 
- cила, действующая на заряд 2 со стороны заряда1. Вектор 
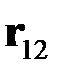направлен от заряда 1 к заряду 2.
Точечный заряд – тело , размерами которого можно пренебречь в данной задаче.
Закон Кулона справедлив для точечных зарядов.
Электрические силы являются дальнодействующими и очень сильными.
Закон Кулона справедлив для покоящихся зарядов.
Закон Кулона проверен вплоть до расстояний порядка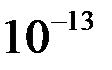 
см.
Кулоновская сила является ньютоновской
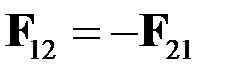
Сила взаимодействия двух зарядов не изменяется при наличии третьего заряда, а также при наличии большего числа зарядов. Это утверждение, проверенное опытным путём носит название принципа суперпозиции.
Электрический заряд-величина инвариантная, она не изменяется при движении заряда.
Электрически заряд аддитивен: заряд любой системы равен сумме зарядов его составляющих.