Плоские электромагнитные волны в диэлектрике

Найдем вид дифференциальных уравнений для Eи H в однородном диэлектрике (величины e и m постоянны, r=0 и j=0). Система уравнений Максвелла в данном случае принимает вид

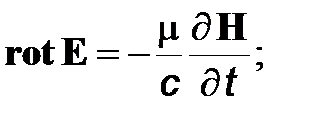(1)

divH=0; (2)

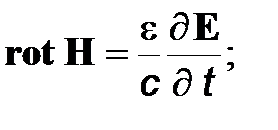(3)

divE=0. (4)

Возьмем ротор от обеих частей (1) и учтем (4). Получим

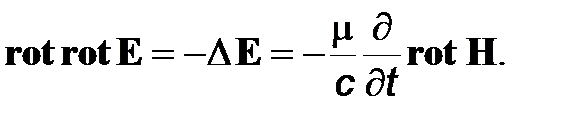(5)

Далее подставим в (5) выражение для ротора поля из (3). Находим

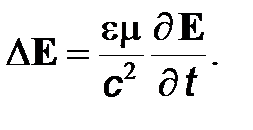(6)

Если взять ротор от обеих частей (3), то с помощью аналогичных преобразований получим

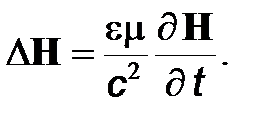(7)

Введем обозначение

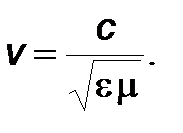(8)

Тогда уравнения (6), (7) принимают стандартный вид волновых уравнений

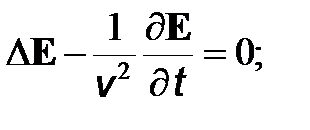(9)

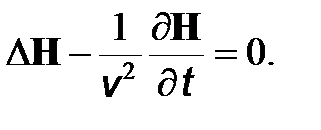(10)

Уже отсюда ясно, что скорость распространения электромагнитных волн в однородном диэлектрике будет определяться по формуле (8). Из этой формулы вытекает, что в вакууме скорость распространения электромагнитных волн совпадает со скоростью света c.

Далее рассмотрим плоские монохроматические волны в однородном диэлектрике, распространяющиеся (для определенности) вдоль оси 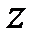. Решение уравнений (9), (10) будем отыскивать в комплексной форме

E=a(z)e^iwt;  H=h(z)e^iwt. (11)

Напомним, что прямой физический смысл имеют только вещественные части этих выражений. Подставив (11) в (9), (10), определим следующие дифференциальные уравнения

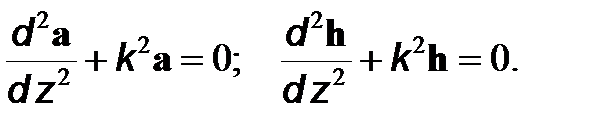(12)

Решения этих уравнений имеют вид

a=a₀e^-ikz+a¢₀e^ikz; h=h₀e^-ikz+h¢₀e^ikz; (13)

В формуле (13) введено обозначение

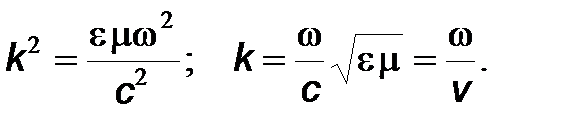(14)

Рассмотрим волну, распространяющуюся в положительном направлении оси Z. Для такой волны окончательно получаем

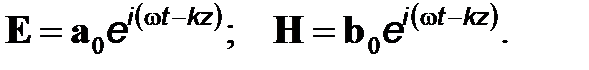(15)

Здесь a₀ и h₀ - амплитуды (вообще говоря, комплексные) векторов E и H. Величину k называют, как обычно, волновым числом. Второе соотношение (14) представляет собой обычную для произвольных плоских монохроматических волн любой природы связь между волновым числом, частотой и скоростью распространения волны.

Вычислим действие оператора Ñ на выражение e^i(wt-kz), входящее в формулы для плоских волн. Находим

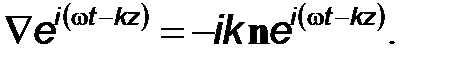(16)

Здесь n–орт оси Z. Легко аналогично определить, что при произвольном направлении распространения плоской монохроматической волны

Ñ=-ikn, (17)

где единичный вектор n совпадает с направлением распространения волны (совпадает с направлением волнового вектора k). На основании соотношения (17) имеем далее

divB=Ñ×(mH)=-ikmnH=0, (18)

divD=-ikenE=0. (19)

Из соотношений (18), (19) вытекает, что векторы E и Hперпендикулярны к направлению распространения волны. Таким образом, плоские электромагнитные волны являются поперечными.

Дифференцирование полей по времени сводится, очевидно, к умножению их на iw. Поэтому из уравнения (1) получаем

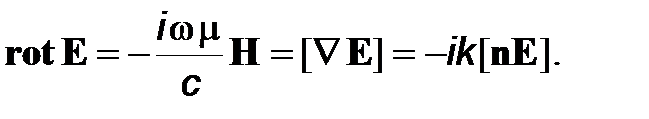(20)

Далее из (20) имеем

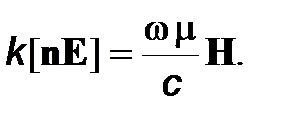(21)

Подставив в (21) выражение (14) для k получим

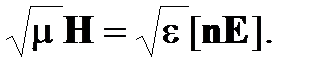(22)

Из уравнения (22) вытекает, что векторы E и H взаимно перпендикулярны. Так как каждый из них перпендикулярен к n, то соотношение (22) также означает, что векторы n, E и H образуют правовинтовую систему. Далее из соотношения (22) вытекает следующее равенство для модулей векторов E и H:

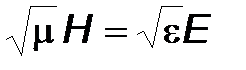(23)

Наконец, из (23) следует, что векторы E и H имеют одинаковые фазы и поэтому изменяются синхронно. Отметим, что для электромагнитной волны в вакууме выполняется особенно простое соотношение

H=E. (24)

Электромагнитная индукция