Возникновение упорядоченности в гидродинамике. Понятия аттрактора и динамического хаоса
Рассмотрим в качестве примера течение воды при термодинамическом равновесии, при малых и больших отклонениях от него. Особенности перехода от ламинарного течения к турбулентному важны для практики, для гидро- и аэромеханики, и они неоднократно решались в рамках физики, механики и математики. Термин «турбулентность» (от лат. turbulentus — беспорядочный) ввел еще Кельвин. Точного описания его нет до сих пор, как нет простой математической модели турбулентных движений, которые оказались связанными с нелинейностью.
В теории обычно имеют дело с безразмерным параметром — числом Рейнольдса Re, введенным в гидродинамические теории (1883) и связанным с режимом течения жидкостей и газов: Re = 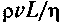 , где v — скорость потока; L — линейный размер, фигурирующий в задаче;
, где v — скорость потока; L — линейный размер, фигурирующий в задаче; 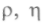 — плотность и динамическая вязкость жидкости. Такие теории (гидро- и аэродинамические) развивали русские ученые Н. Е.Жуковский, С. А.Чаплыгин и др. Одна из наиболее стройных теорий перехода к турбулентности была построена в 1944 г. Л.Д.Ландау. Вообще, это явление очень сложное, можно сказать, что это целый комплекс связанных явлений.
— плотность и динамическая вязкость жидкости. Такие теории (гидро- и аэродинамические) развивали русские ученые Н. Е.Жуковский, С. А.Чаплыгин и др. Одна из наиболее стройных теорий перехода к турбулентности была построена в 1944 г. Л.Д.Ландау. Вообще, это явление очень сложное, можно сказать, что это целый комплекс связанных явлений.
При равновесии, если система замкнута и v = 0, ее энтропия максимальна. При наличии градиента давления жидкость течет в сторону меньших давлений, ее движение происходит как бы слоями, параллельными направлению течения (ламинарное течение). Потоки и термодинамические силы связаны линейно, производство энтропии в стационарном состоянии (течении) минимально. При малых значениях числа Re единственная стационарная картина течения соответствует ламинарному течению. Небольшие отклонения скоростей движения от стационарных значений, возникающие из-за флуктуации, экспоненциально затухают со временем, появляется пара вихрей. При увеличении скорости потока выше критической некоторые из малых возмущений перестают затухать, система теряет устойчивость и переходит в новый режим; вихри начинают осциллировать, движение жидкости становится турбулентным. Линейная зависимость потоков и сил нарушается, как и теорема Пригожина о минимальном приросте энтропии, хотя картина еще стационарна. В этом случае говорят о
первой бифуркации (в пер. — раздвоение, разветвление), или бифуркации Хопфа.
С увеличением числа Re новый периодический режим вновь теряет устойчивость, возникают незатухающие колебания с частотой, определяемой величиной Re. Растет неравновесность, и вместе с ней число корреляций и параметров, характеризующих систему. При переходе к турбулентности между отдельными областями течения возникают новые корреляции, новые макроскопические связи. Затем появляются новые частоты, сокращается интервал частот, и, по теории Ландау, появляющиеся новые движения имеют все более мелкие масштабы. Нерегулярное поведение, типичное для турбулентности, — результат бесконечного каскада бифуркаций. Говорят, что система из «царства необходимости» переходит в «царство свободы». Но и в «царстве свободы» периодически возникают области, где движение вновь приобретает порядок — «острова необходимости».
При существенном усложнении структуры течения одновременно увеличивается его внутренняя упорядоченность. Это уже не тот беспорядок, что был в равновесном состоянии. Существенно меняется характер броуновского движения частиц, турбулентность сказывается на поглощении и рассеянии электромагнитных и звуковых волн. Например, фотографии распределения световой волны, прошедшей через турбулентную жидкость, фиксируют пятна типа интерференционной картины, соответствующей фокусам и каустикам, которые возникают в световом пучке.
Проблема турбулентности важна не только в связи с инженерными приложениями. Большая часть среды Вселенной находится в турбулентном движении, и с неустойчивостями сталкиваются в физике атмосферы и астрофизике, в океанологии и физике планет. Вообще отношение к хаосу было разнообразным. У древних греков хаос считался первичным состоянием материи, но, как отметил Б. Пастернак, «напрасно в годы хаоса искать конца благого».
Хаотические эффекты, нарушавшие стройную картину классической физики с первых дней становления теории, в XVII в. воспринимались как досадные недоразумения. Кеплер отмечал нерегулярности в движении Луны вокруг Земли. Ньютон, по словам своего издателя Р. Котеса, принадлежал к тем исследователям, которые силы природы и простейшие законы их действия «выводят аналитически из каких-либо избранных явлений и затем синтетически получают законы остальных явлений». Но закон — однозначное и точное соответствие между рассматриваемыми явлениями, он должен исключать неопределенность и хаотичность. Отсутствие однозначности в науке того времени рассматривалось как свидетельство слабости и ненаучного подхода к явлениям. Постепенно из науки изгонялось все, что нельзя формализовать, чему нельзя придать однозначный характер. Так пришли к механической картине мира и «лапласовскому детерминизму».
Необратимость процессов нарушила универсальный характер механических законов. Поскольку проследить за движением каждой молекулы газа невозможно, пришлось признать ограниченность своих возможностей и согласиться, что закономерности, наблюдаемые в поведении массы газа как целого, есть результат хаотического движения составляющих его молекул. И тогда Клаузиус ввел «принцип элементарного беспорядка», который понимался как независимость координат и скоростей отдельных частиц друг от друга при равновесии. Эту идею Больцман и положил в основу своей молекулярно-кинетической теории. Максвелл указал на принципиальное отличие механики отдельной частицы от механики большой совокупности частиц, подчеркнув, что большие системы характеризуются параметрами (давление, температура и др.), не применимыми к отдельной частице. Так родилась новая наука — статистическая механика. Идея элементарного беспорядка, или хаоса, устранила противоречие между механикой и термодинамикой. На основе статистического подхода удалось совместить обратимость отдельных механических явлений (движений отдельных молекул) и необратимый характер движения их совокупности (рост энтропии в замкнутой системе).
Но идеи хаоса оказались более фундаментальны. При изучении теплового излучения возникли противоречия: электромагнитная теория Фарадея — Максвелла описывала обратимые процессы, но процессы обмена световой энергией между телами, находящимися при разных температурах, ведут к выравниванию температур, т. е. должны рассматриваться как необратимые. Планк ввел гипотезу «естественного излучения», соответствующую гипотезе молекулярного беспорядка. Ее смысл такой: отдельные электромагнитные волны, составляющие тепловое излучение, ведут себя независимо и «являются полностью некогерентными». Эта гипотеза привела к представлению о квантовом характере излучения, которое обосновывалось с помощью теории вероятностей. Хаотичность излучения оказалась связанной с его дискретностью. Квантовый подход позволил Планку и Эйнштейну объяснить ряд законов и явлений (закон Стефана — Больцмана, закон смещения Вина, законы фотоэффекта и др.), которые не находили объяснения в классической электродинамике.
Отступления Луны от траекторий, рассчитанных по законам классической механики, американский астроном Дж.Хилл в конце XIX в. объяснил притяжением Солнца. Французский математик А. Пуанкаре предположил, что вблизи каждого тела есть малозаметные факторы и явления, вызывающие нерегулярности. Поведение даже простой системы существенно зависит от начальных условий, так что не все можно предсказать. Решая задачу трех тел, Пуанкаре обнаружил существование фазовых траекторий, которые вели себя запутанно и сложно, образуя «нечто вроде решетки, ткани, сети с бесконечно тесными петлями; ни одна из кривых никогда не должна пересечь самое себя, но она должна навиваться на самое себя очень сложным образом, чтобы пересечь
много, бесконечно много раз петли сети». В начале XX в. на эту работу особого внимания не обратили.
Примерно в это же время Планк начал изучать другую хаотичность классической науки и нашел выход во введении кванта, который должен был примирить прежние и новые представления, но на самом деле сокрушил классическую физику. В строении атомов долгое время видели аналогию со строением Солнечной системы. Интерес к невозможности однозначных предсказаний возник в связи с появлением принципиально иных статистических законов движения микрообъектов. Соотношения неопределенности Гейзенберга показывают, что может реализовываться лишь некоторая конечная область состояний 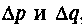 , внутри которой
, внутри которой
лежат начальные координаты q0 и импульсы р0. При этом внутри выделенной области значения координат и импульсов распределены по вероятностному закону, и по мере эволюции системы увеличивается и область ее состояний 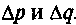 . На небольших вре-
. На небольших вре-
менных интервалах неопределенность состояния будет нарастать медленно и движение системы будет устойчивым. Для таких систем классическая механика плодотворна.
В 60-е гг. XX в. была установлена возможность случайных явлений, от которых нельзя избавиться уточнением начальных условий и исчерпывающим описанием воздействий на систему, и в простых динамических системах, которые считались со времен Ньютона и Лапласа подчиняющимися определенным и однозначным законам механики. Такие движения возникают в механических и электрических нелинейных колебательных системах. Пример такого неустойчивого движения — шарик в двух ямках, разделенных барьером (рис. 13.1). При неподвижной подставке шарик имеет два положения равновесия. При колебаниях подставки он может начать перепрыгивать из одной ямки в другую после совершения колебаний в одной из ямок. После нескольких затухающих колебаний шарик займет в одной из ямок положение, называемое устойчивым равновесием. Периодические колебания с оп-
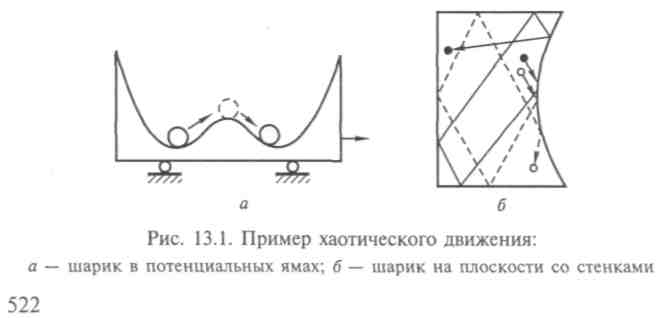
ределенной частотой вызывают колебания с широким спектром частот. Положение же на границе между ямками будет неустойчивым равновесием. Физический смысл этих понятий применим к равновесию любых систем. Режим функционирования динамической системы устойчив, если малые возмущения затухают со временем, стремясь к нулю. Если же они нарастают — режим неустойчивый.
Кроме того, на систему могут действовать и некоторые случайные силы, которые даже при самой малой величине за длительное время действия приведут к непредсказуемым результатам. Такие системы чувствительны не только к начальным значениям параметров, но и к изменениям положений и скоростей в разных точках траектории. Получается парадокс: система подчиняется однозначным динамическим законам и совершает непредсказуемые движения. Решения динамической задачи реализуются, если они устойчивы. Например, нельзя видеть сколь угодно долго стоящий на острие карандаш или монету, стоящую на ребре. Но тогда задача из динамической переходит в статистическую, т. е. следует задать начальные условия статистическим распределением и следить за его эволюцией. Эти случайные явления получили название динамического хаоса.
В 1963 г. метеоролог Э.Лоренц описал новый механизм потери устойчивости, наблюдаемый в процессе конвекции при моделировании процессов возникновения турбулентности. Он обнаружил в фазовом пространстве трех измерений (координаты — скорость и амплитуды двух температурных мод) область, которая как бы притягивала к себе траектории из окрестных областей. Попадая в область, названную им странным аттрактором (лат. attractio — притяжение), близкие траектории расходились и образовывали сложную и запутанную структуру. Переход системы на такой режим означает, что в ней наблюдаются сложные непериодические колебания, очень чувствительные даже к малому изменению начальных условий. Эта чувствительность к малому воздействию получила красочное название — «эффект бабочки». Значит, небольшие флуктуации, подобные взмаху крыльев бабочки, могут вызвать хаотические режимы. Так как две близкие траектории разбегаются в фазовом пространстве, то предсказание движения по начальным данным не может быть точным. С этим связаны трудности предсказания погоды. До Лоренца советские математики Д. В.Аносов и Я. Г. Синай установили существование таких областей и исследовали устойчивость явлений в них.
Возникновением динамического хаоса считается переход к турбулентности, поскольку течение жидкости описывается детерминистическими уравнениями. Но детерминированность подразумевает однозначную связь причины и следствия,
предсказуемость и воспроизводимость, а когда говорят о хаосе, понимают нечто прямо противоположное. Но это понятие не столь простое. Обратимся для примера к броуновской частице. Под действием случайных толчков со стороны соседних молекул частица будет совершать непредсказуемые блуждания, и ее траектория будет выглядеть запутанной (что и наблюдается под микроскопом). Но при многократном наблюдении можно заметить, что эта запутанная траектория не повторяется даже при одинаковых начальных условиях, что соответствует интуитивным представлениям о хаосе.
