Кинематические характеристики вращательного движения. Угловая скорость и угловое ускорение
При вращательном движении все точки тела описывают окружности, при этом радиус-векторы поворачиваются на угол 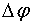 за время
за время 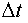 . Для того, чтобы указать, в какую сторону совершается поворот, элементарные повороты изображают в виде вектора
. Для того, чтобы указать, в какую сторону совершается поворот, элементарные повороты изображают в виде вектора 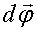 . По модулю
. По модулю 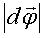 равен величине угла поворота, а направление подчиняется правилу правого винта (рис. 1.6). Быстроту вращения характеризует угловая скорость
равен величине угла поворота, а направление подчиняется правилу правого винта (рис. 1.6). Быстроту вращения характеризует угловая скорость 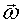 .
.
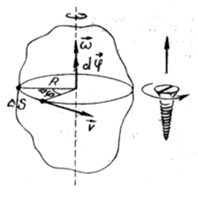
Рис.1.6
Угловой скоростью называется производная от угла поворота по времени.
Модуль угловой скорости равен
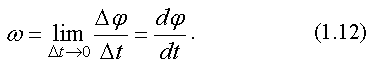
Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта (рис. 1.6). При равномерном вращении угловая скорость 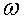 связана с периодом обращения Т и частотой вращения
связана с периодом обращения Т и частотой вращения 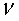 следующим образом
следующим образом

Модуль угловой скорости выражается в радианах в секунду (рад/с). Быстрота изменения угловой скорости характеризуется угловым ускорением 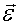 .
.
Угловым ускорением называется производная от угловой скорости по времени. Модуль углового ускорения равен

При вращении тела вокруг неподвижной оси угловое ускорение 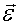 также как и угловая скорость
также как и угловая скорость 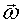 направлено вдоль оси вращения. При ускоренном движении эти вектора сонаправлены
направлено вдоль оси вращения. При ускоренном движении эти вектора сонаправлены 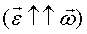 , при замедленном - противоположны
, при замедленном - противоположны 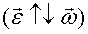 . Угловое ускорение измеряется в рад/с2.
. Угловое ускорение измеряется в рад/с2.
При равномерном вращении
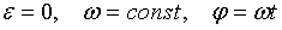 .
.
При равнопеременном вращении
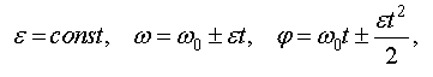
где 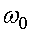 - начальная угловая скорость.
- начальная угловая скорость.
Знак "+" - при равноускоренном движении.
Знак "-" - при равнозамедленном движении.
1.1.8. Связь между линейной и угловой скоростью, линейным и угловым ускорением
При вращении твердого тела вокруг неподвижной оси линейные скорости 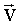 и линейные (тангенциальные) ускорения
и линейные (тангенциальные) ускорения 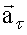 для различных его точек будут различны. Угловая скорость
для различных его точек будут различны. Угловая скорость 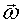 и угловое ускорение
и угловое ускорение 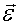 будут одинаковыми для всех точек вращающегося тела.
будут одинаковыми для всех точек вращающегося тела.
Для того чтобы найти связь между модулями линейной и угловой скорости нужно использовать известное в геометрии соотношение между центральным углом 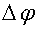 и дугой, на которую он опирается (рис. 1.6)
и дугой, на которую он опирается (рис. 1.6)
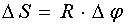 .
.
Отсюда:
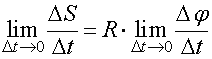 .
.
Используя формулы (1.5) и (1.12), получим

Формула (1.15) показывает, что линейная скорость равна угловой, умноженной на радиус.
Чтобы найти связь между модулями линейного (тангенциального) и углового ускорений, продифференцируем формулу (1.15)
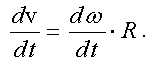
Воспользуемся формулами (1.10) и (1.14) и получим

Из формулы (1.16) следует, что линейное (тангенциальное) ускорение равно угловому, умноженному на радиус.
Задания и вопросы для самоконтроля
1. На какие разделы делится механика?
2. Какие простейшие модели используются в механике?
3. Что называется поступательным движением? Вращательным?
4. Как определяют положение точки в пространстве?
5. Чем отличаются путь и перемещение?
6. Какие Вы знаете кинематические характеристики поступательного движения? Дайте определение скорости, ускорения.
7. Что характеризует нормальное ускорение? Что тангенциальное? Как они вычисляются?
8. Как вычисляются скорость и путь при поступательном движении?
9. Расскажите о кинематических характеристиках вращательного движения. Дайте определение угловой скорости и углового ускорения.
10. Как связаны линейные и угловые характеристики?
