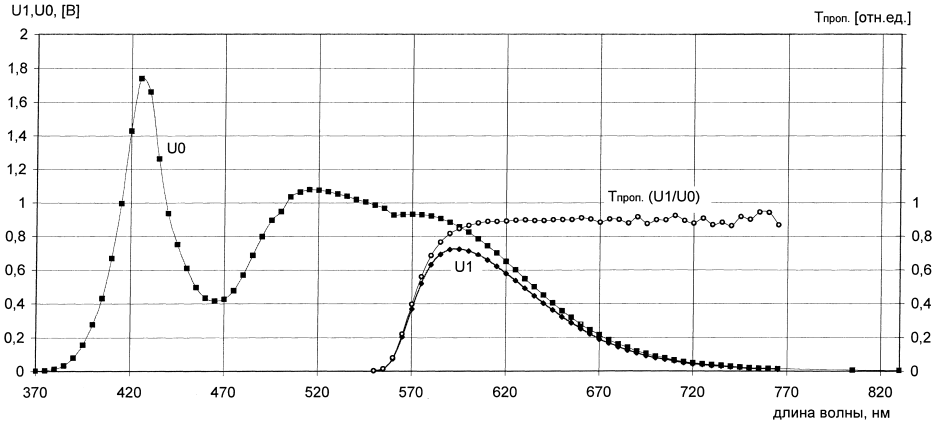
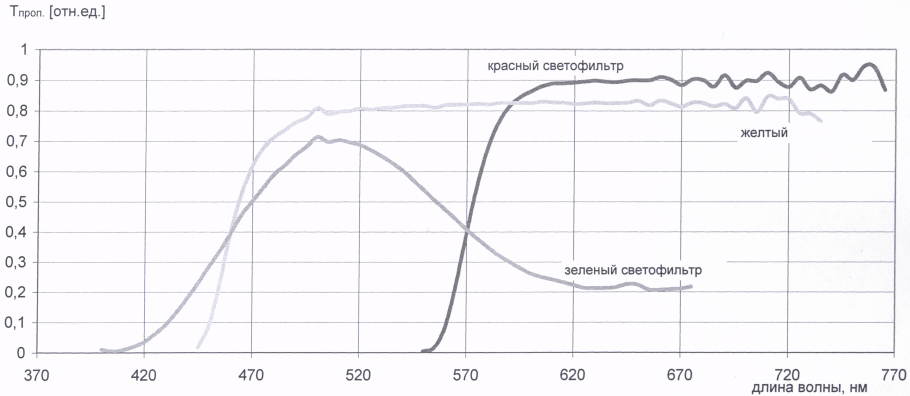
Спектр пропускания красного светофильтра

ПРИЛОЖНИЕ 2

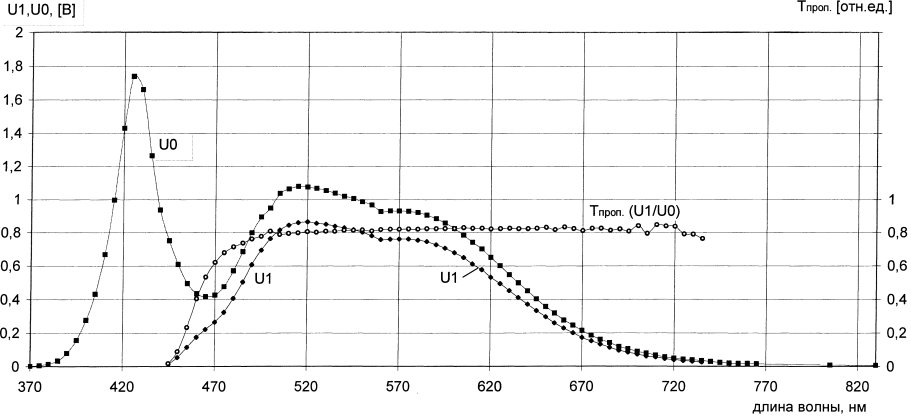
Спектр пропускания желтого светофильтра

ПРИЛОЖНИЕ 3

Спектр пропускания зеленого светофильтра

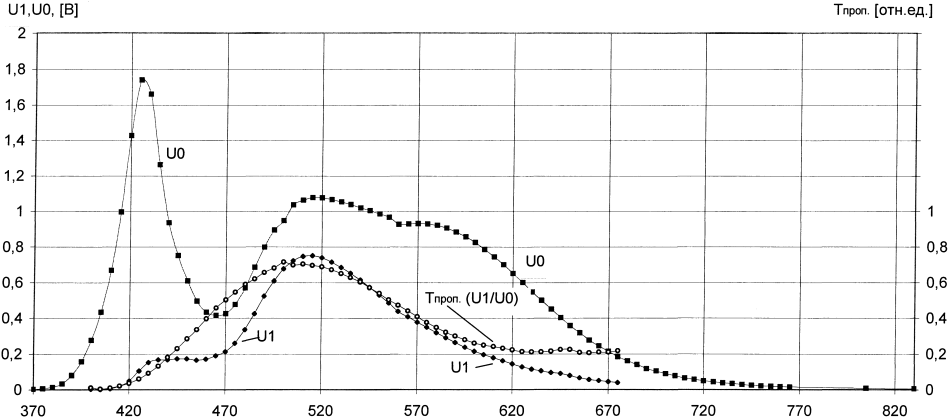
Длина волны, нм

ПРИЛОЖЕНИЕ 4

ЛАБОРАТОРНАЯ РАБОТА № 3.30

ИССЛЕДОВАНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ СВЕТА

Цель работы: ознакомление с дифракционными картинами различных типов, определение углов дифракции света и ширины дифракционной щели.

Теоретические положения

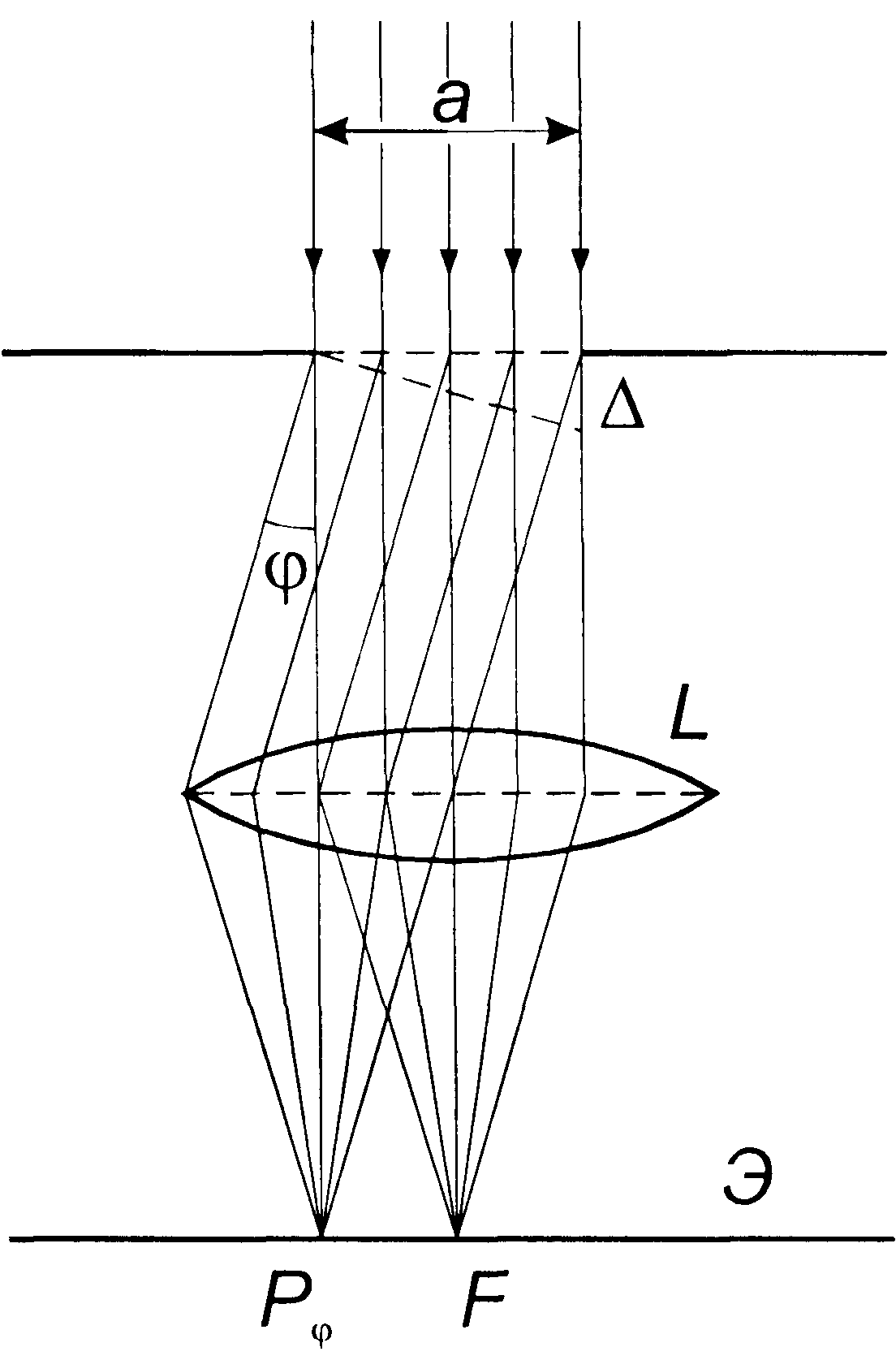Рассмотрим дифракцию плоской монохроматической вол­ны от щели. Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины. Обозначим ширину щели а (рис. 3.30.1).

Рис. 3.30.1.

Световая волна длиной λ падает нормально к плоскости щели. За щелью установлена собирательная линза L, в фокаль­ной плоскости которой находится экран Э. Параллельный пучок лучей, пройдя через щель, дифрагирует под разными углами вправо и влево от первоначального направления. Линза собира­ет параллельные пучки дифрагированных лучей в соответст­вующих точках экрана Э. Тип дифракции, при котором рас­сматривается дифракционная картина, образованная параллель­ными лучами, получил название дифракции в параллельных лу­чах, или дифракции Фраунгофера.

Расчет дает формулу распределения интенсивности света на экране Э в зависимости от угла дифракции φв виде:

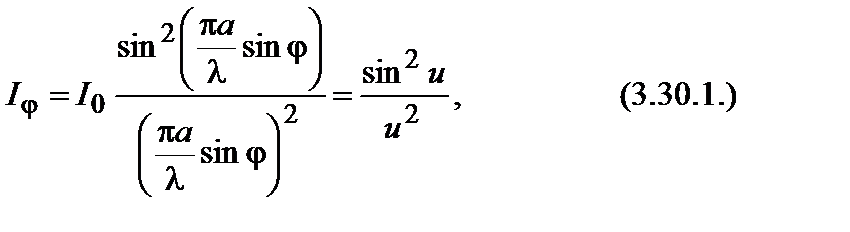
где 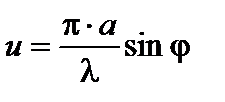, I₀ – интенсивность света в середине дифракционной картины (в направлении φ=0); I – интенсивность света в точке, положение которой определяется данным значением угла φ. При значении угла дифракции φ, удовлетворяющего условию

где k = ± 1,2, 3, ..., интенсивность света равна нулю. Послед­нее условие и количественные соотношения можно полу­чить при решении задачи о дифракции на щели методом графического сложения амплитуд.

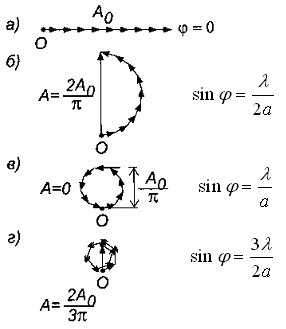
Рис. 3.30.2.

Разобьем открытую часть волновой поверхности на ряд узких параллельных полосок равной ширины. Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Выражая амплитуды каждой полоски векторами рав­ной длины, найдем результирующую амплитуду, пользуясь графическим методом сложения амплитуд. Результаты при разных углах дифракции φпредставлены на рис. 3.30.2.

При φ=0(рис. 3.30.2а), т.е. в фокусе линзы L, амплитуда колебаний A₀ будет максимальной.

В направлении, при котором крайние полоски отличаются по фазе на π(Δ=λ/2), результирующая амплитуда равна 2A₀/π (рис. 3.30.2б), так как последняя равна диаметру полуокружности, длина которой A₀.

В направлении, при котором крайние полоски отличаются по фазе на 2π (Δ=λ),результирующая амплитуда об­ращается в нуль (рис. 3.30.2в). Амплитуда равна нулю во всех случаях, когда разность хода меж­ду крайними лучами Δравна λ, 2λ, 3λ, ..., kλ, т.е. минимумы освещенности соответствуют направлениям

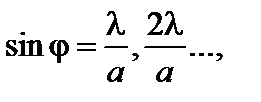(3.30.3)

где k – целое число, так как Δ = a sin φ.

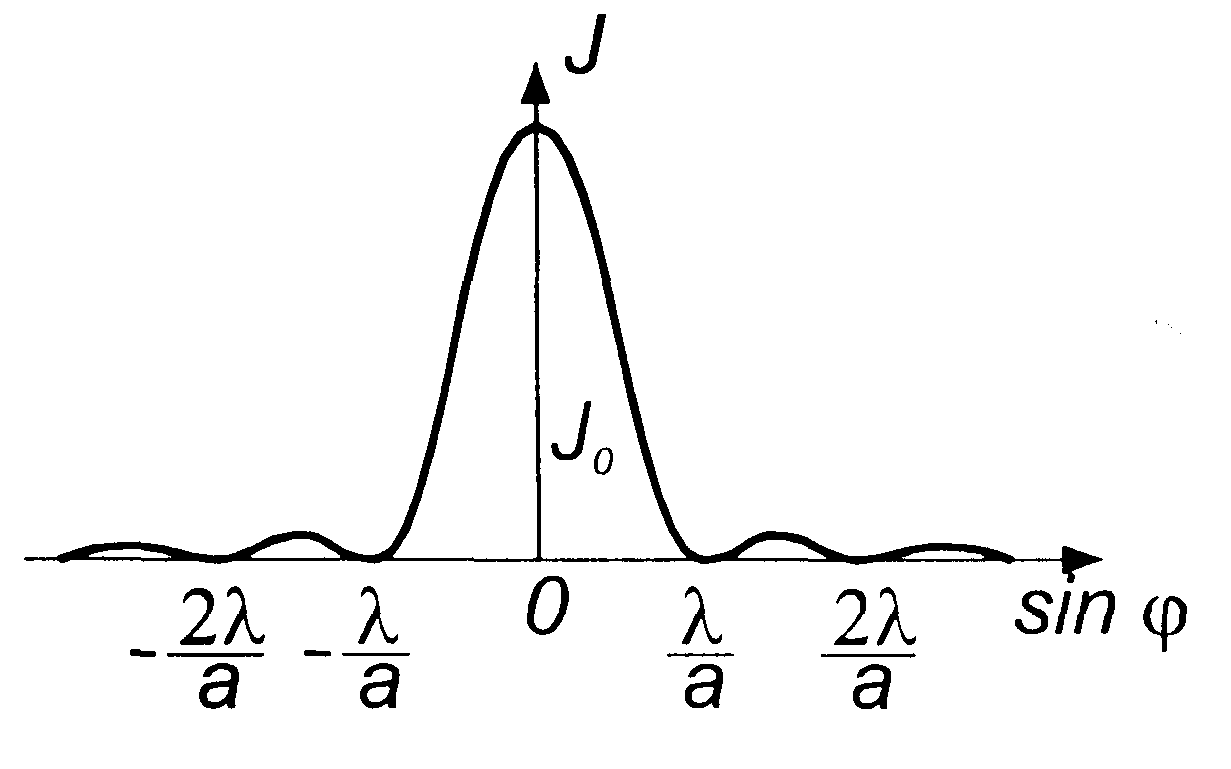
Распределение освещенности в фокальной плоскости линзы L представлено на рис.3. Центральная светлая полоса (максимум нулевого порядка) занимает область между ближайшими правыми и левыми минимумами, т.е. область между

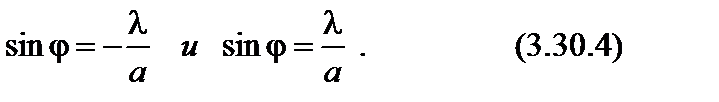
Интенсивность света I₀ определяется квадратом А₀. Следующие максимумы значительно уступают по величине центральному.

Рис.3.30.3.

Действительно, при 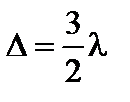амплитуда колебаний 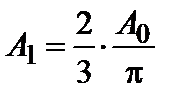(рис. 3.30.2г), интенсивность первого максимума

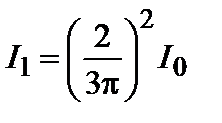(3.30.5)

или

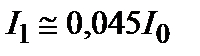. (3.30.6)

Аналогично можно найти и интенсивности остальных максимумов. Расчеты показыва­ют, что интенсивности центрального и следующих максимумов относятся как 1 : 0,045 : 0,016 и т.д.

Рис. 3.30.4.

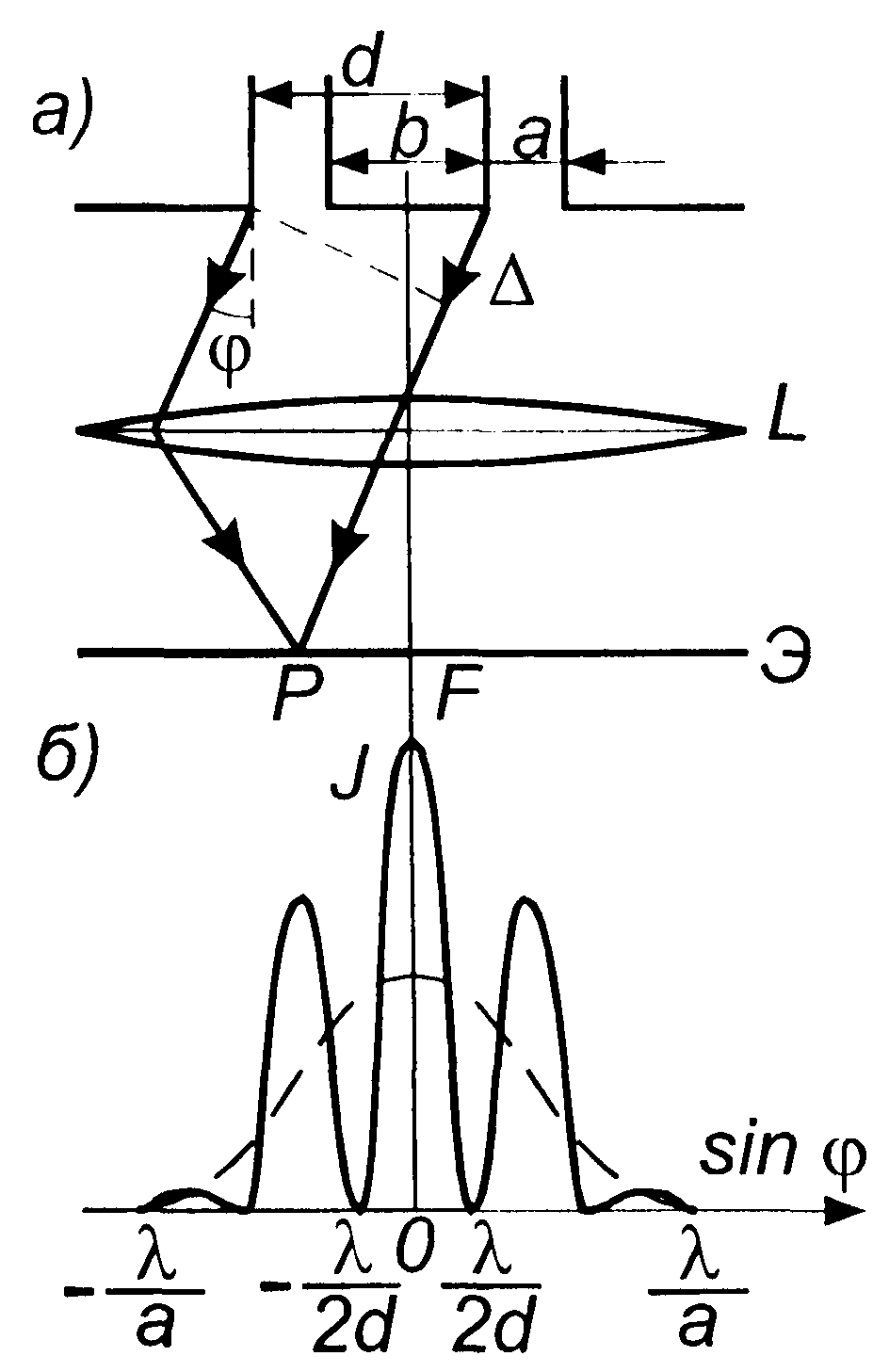Рассмотрим дифракцию от двух параллельных щелей одинако­вой ширины а и расположенных на расстоянии b друг от друга. Ди­фракционная картина наблюдается в фокальной плоскости линзы L. (рис. 3.30.4а). На экран со щелями падает плоская монохроматическая волна длиной λ. Положение дифракционных максимумов и миниму­мов от одной щели не зависит от ее положения, а определяется на­правлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракци­онной картины. Следовательно, картины, создаваемые каждой ще­лью в отдельности, будут совершенно одинаковыми.

Результирующую картину можно определить путем сложения этих двух картин с учетом интерференции волн, идущих от каждой из щелей. Очевидно, что в тех направлениях, в которых ни одна из щелей света не дает света, не будет света и при двух параллельных щелях. Условие минимума интенсивности a sin φ = = kλ, где k = ±1, 2, 3, ..., выполняется и в данном случае. Кроме того, возможны направления, в которых коле­бания, посылаемые двумя щелями, взаимно уничтожаются. Возникают добавочные миниму­мы. Они будут наблюдаться в тех направлениях, которым соответствует разность хода

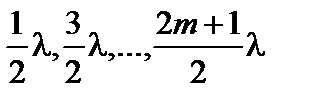
для волн, идущих от соответственных точек (отстоящих на расстоянии а + b) обеих щелей. Такие направления определяются (см. рис. 3.30.4) условием

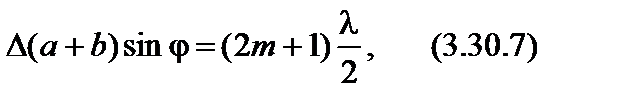
где m = ± 0, 1, 2, 3, .... В направлениях, определяемых из условий

(a + b) sin φ = 0, λ, 2λ, ..., mλ, где m = ± 0, 1, 2,..., (3.30.8)

действие одной щели усиливает действие другой. Этим направлениям соответствуют максимумы интенсивности. Расстояния между первичными минимумами (от одной щели) зависит от ширины щели а. Если а << (а +b), то между двумя первичными минимумами может расположиться несколько минимумов и максимумов. Кривая на рис. 4,б показывает распре­деление интенсивностей света при дифракции на двух параллельных щелях.

Если ширина щели а значительно меньше расстояния от щели до экрана, дифракция Фраунгофера будет иметь место и при отсутствии линзы между щелью и экраном (падающая на щель волна должна быть плоской). В этом случае лучи, идущие в точку Р от краев щели, будут практически параллельны, так что все полученные ранее результаты остаются спра­ведливыми.

Измерив на опыте по дифракционной картине от узкой щели ширину центрального максимума и зная длину волны источника света, можно определить ширину щели. По карти­не дифракции от двух параллельных узких щелей, зная длину волны источника и ширину каждой щели, можно определить расстояние между ними.

В более общем случае при дифракции на совокупности N щелей одинаковой ширины а и расположенных на расстоянии b друг от друга выражение для интенсивности дифрагиро­вавших лучей имеет вид

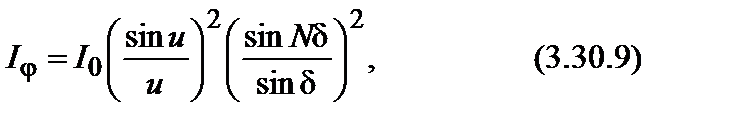
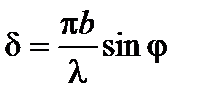
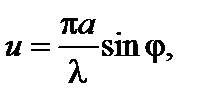
где

Формулу (3.30.9) можно представить в виде произведения двух членов. Первый член, на­зываемый дифракционным, имеет вид:

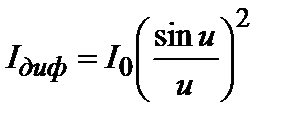(3.30.10)

и описывает дифракцию на одной щели размера а. Вид этой функции совпадает с приведен­ным на рис.3. Второй член, равный

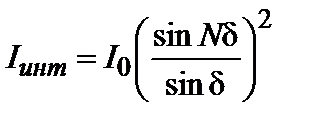, (3.30.11)

описывает интерференцию излучения, приходящего от различных щелей, и носит название интерференционного.

Числитель в формуле (3.30.11) обращается в нуль при

δ=0, π/N, 2π/N, …, (N-l)π/N, π, (N+1)π/N,...

однако для каждого N-гo значения 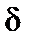= 0, π, 2π, ... в нуль обращается и знаменатель. Воспользовавшись предельным переходом, можно получить, что для этих значений уг­ла функция (3.30.11) имеет одинаковое максимальное значение, равное N². Таким образом, для этих значений угла δ интенсивность будет максимальной. Между этими максимумами, назы­ваемыми главными, располагаются (N – 1)добавочных минимумов, соответствующих нуле­вым значениям числителя в формуле (3.30.11). Так как между любыми двумя соседними добавоч­ными минимумами имеется добавочный максимум, интенсивность которого существенно меньше интенсивности ближайших главных максимумов, то общее число добавочных мак­симумов между главными равно (N – 2).

Вид функции (3.30.11), описывающей распределение интенсивности при дифракции Фраун­гофера на N = 4 щелях, изображен на рис. 3.30.5в. Характерными точками этого графика являются:

главные дифракционные минимумы	sinφ =λ /b, 2λ /b, 3λ /b,…
добавочные интерференционные минимумы	sinφ = λ /Nd, 2λ /Nd, 3λ /Nd, ...., (N-1)λ /Nd, (N+1)λ /Nd,..., (2N-1)λ /Nd, (2N+1)λ /Nd,...
главные интерференционные максимумы	sinφ = 0, λ /d, 2λ /d, 3λ /d, ....

Таким образом, получив на экране дифракционную картину от решетки и подсчитав число добавочных минимумов или максимумов между главными максимумами, можно оп­ределить число щелей решетки.

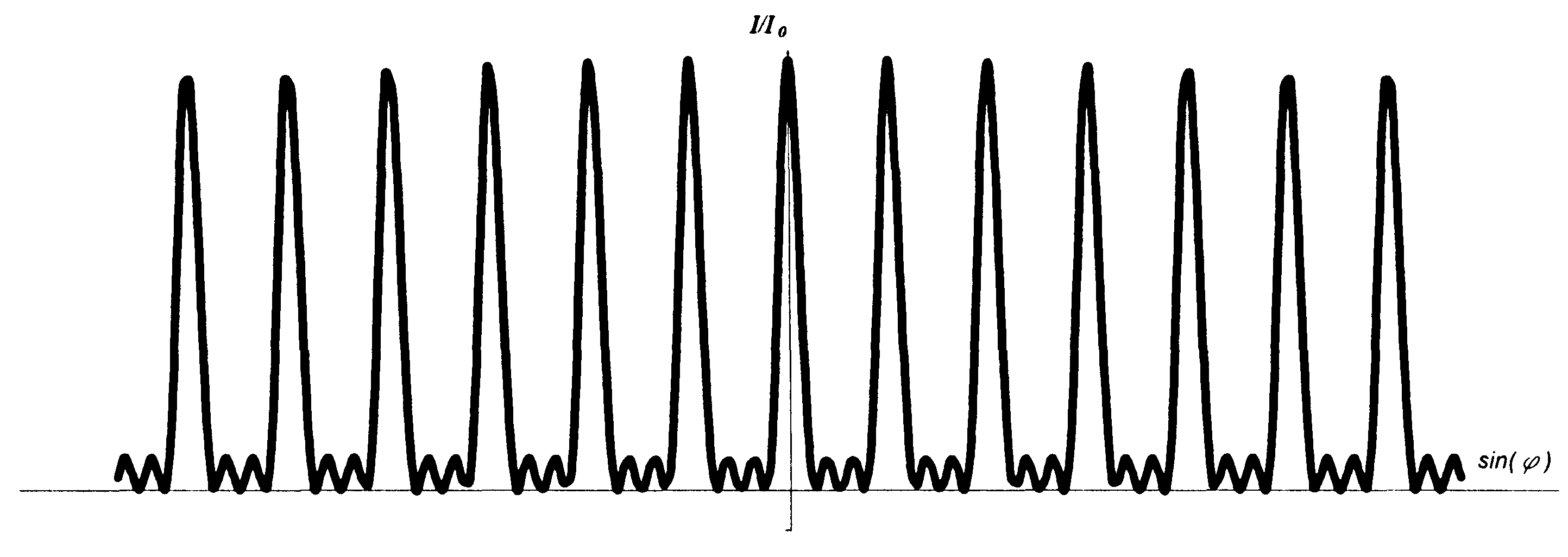
а)

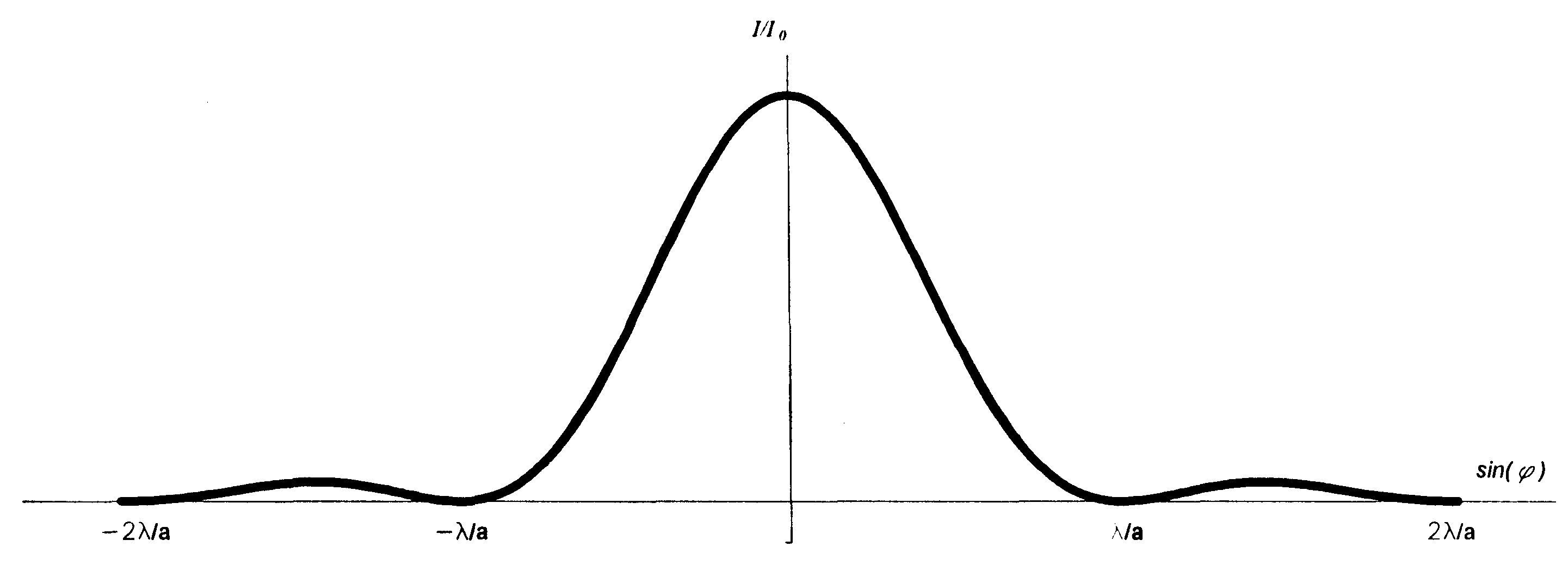
б)

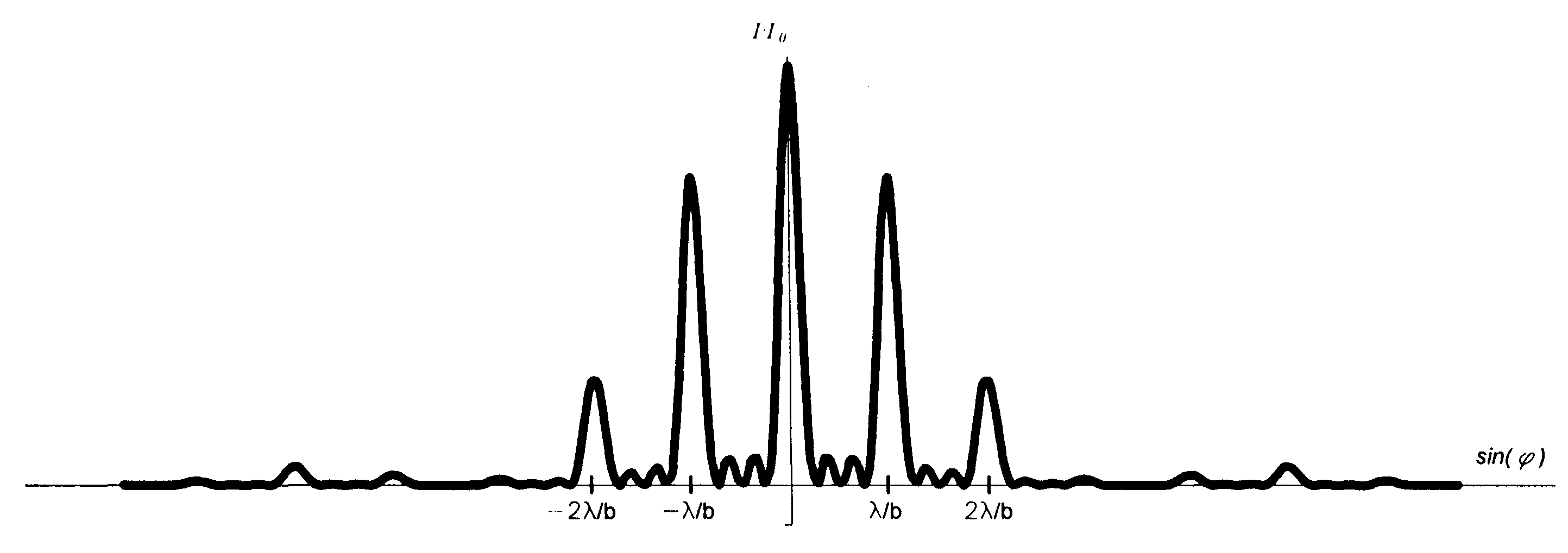
в)

Рис. 3.30.5. Дифракция Фраунгофера на четырех щелях:

а – интерференционный член (5), б – ди­фракционный член (4),

в – общий вид дифракционной картины (3).