Ii. работа с фазовой пластинкой

1. Вращением установить анализатор в такое положение, чтобы полностью погасить свет, попадающий на фотоприемник.

2. Поместить перед анализатором фазовую пластинку.

3. Вращая пластинку вокруг своей оси, убедиться в наличии таких четырех ее положений, в которых опять будет наблюдаться полное гашение света. Эти положения соответствуют ориентации одной из собственных осей пластинки перпендикулярно плоскости главно­го пропускания анализатора.

4. Выбрав любое из таких положений, повернуть пластинку на 45° и закрепить ее в этом положении. В указанном случае мы получаем, что плоскость поляризации падающего излучения ориентирована под углом 45° к собственным осям пластинки, и, таким образом, амплитуды обыкновенного и необыкновенного лучей одинаковы.

5. Вращая анализатор, снять показания с мультиметра аналогично первой части работы и заполнить табл. 2.

Таблица 2

Угол φ

…

I, мА

I0 = <I> – IT

Обработка результатов

1. Построить график зависимости I₀ = f(φ).

2.Найти средние значения I_min и I_mах.

3. Рассчитать эллиптичность, равную отношению малой и большой полуосей эллипса, которая выразится следующим образом:

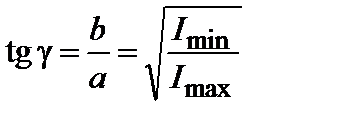(3.26.10)

4. При выполнении условия ориентации осей фазовой пластинки под углом 45° к плоскости поляризации падающего света (п. 4) разность фаз δи εсвязаны между собой простым соотношением: δ = 2γ. Данная формула следует из выражений (6), (8) а также иллюстрирует­ся следующими примерами: при разности фаз между обыкновенным и необыкновенным лучом δ = 0 или δ = π,как было описано выше, эллипс вырождается в прямую – эллиптичность обращается в ноль или бесконечность

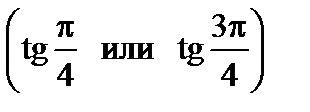
и эллипс превращается в круг.

5. При известной толщине пластинки из слюды можно рассчитать разность показате­лей преломления обыкновенного и необыкновенного лучей (п₀ – п_е).

Контрольные вопросы

1. Что такое естественный и поляризованный свет?

2. Что такое плоскополяризованный и частично поляризованный свет и плоскость поляризации?

3. Что такое поляризатор и анализатор?

4. Что такое эллиптическая поляризация света?

5. Как формулируется закон Малюса?

6. Как плоскополяризованный свет проходит через кристаллическую пластину?

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

2. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.

3. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. –560 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.27

ИССЛЕДОВАНИЕ ДИСПЕРСИИ

ОПТИЧЕСКОГО СТЕКЛА

Цель работы: определение показателей преломления оптического стекла для различных длин волн и построение кривой дисперсии.

Теоретические положения

Дисперсией света принято называть зависимость показателя преломления вещества от длины волны или от частоты электромагнитных световых колебаний. Это явление объясняется разной фазовой скоростью распространения в веществе световых волн различной длины. Показатель преломления вещества представляет собой отношение фазовой скорости света в вакууме к его фазовой скорости в данной среде n = c/v. Если скорость света в среде зависит от длины волны, то и показатель преломления среды должен зависеть от длины волны. Дисперсией обладают практически все прозрачные среды, кроме вакуума, в котором скорость рас­пространения всех электромагнитных волн любой длины одинакова.

Всякий метод, который применяется для определения показателя преломления (пре­ломление в призмах, полное внутреннее отражение, интерференционные методы), может служить для обнаружения явления дисперсии.

В данной работе измерение показателей преломления производится для оптического стекла, имеющего форму призмы. Разложение белого света в спектр при прохождении его через призму вызвано явлением дисперсии. Свет разных длин волн (разного цвета) неоди­наково преломляется на границе двух прозрачных сред, так как n = f(λ) .

Для оптической призмы существует связь угла отклонения лучей призмой от их пер­воначального направления δс показателем преломления стекла призмы n, преломляю­щим углом призмы А и углом падения лучей на призму α. Используя эту зависимость, можно определить показатели преломления вещества призмы. Данный метод и применя­ется в работе.

Рис. 3.27.1.

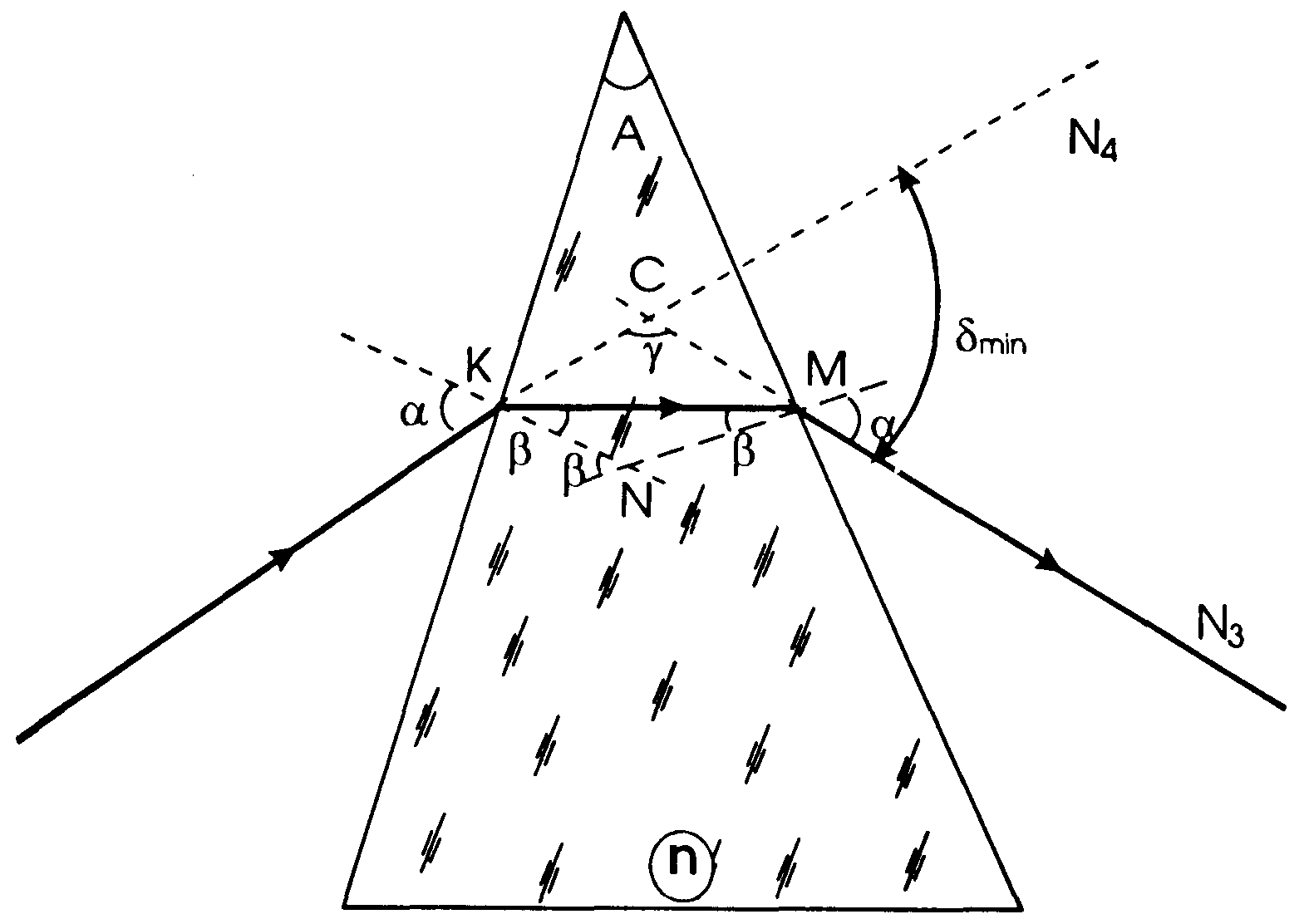При некотором определенном угле падения лучей на призму угол отклонения лучей призмой δ принимает наименьшее значение и носит название угла наименьшего отклонения δ_min. В этом случае угол падения лучей на призму α(рис. 3.27.1) равен углу их выхода из призмы, то есть луч в призме идет параллельно основанию. Установим для это­го случая связь п, А и δ_min .

Запишем закон преломления света для входной грани призмы

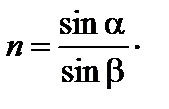(3.27.1)

Из рис. 3.27.1 следует, что

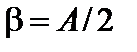, (3.27.2)

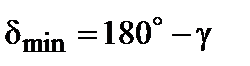, (3.27.3)

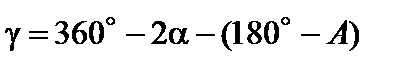(3.27.4)

из четырехугольника NKCM,

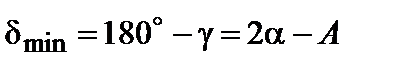. (3.27.5)

Отсюда

. (3.27.6)

Подставляя значения β и αв закон преломления, получаем

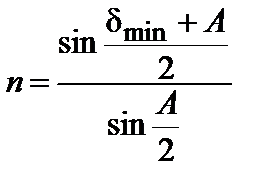. (3.27.7)

Из формулы видно, что в работе должны быть измерены углы А и δ_min для различ­ных длин волн и затем рассчитаны значения показателя преломления.

Описание оборудования

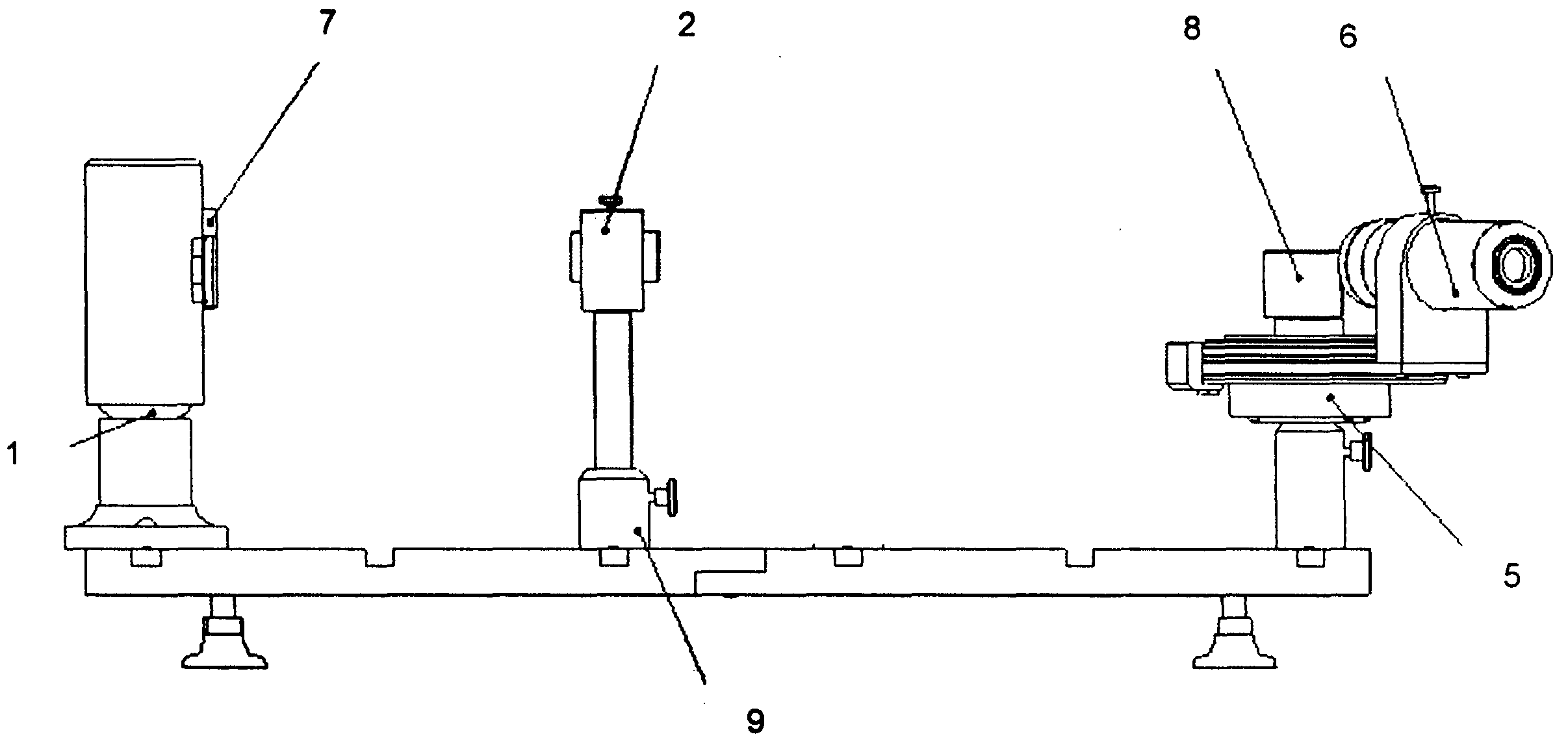Установка смонтирована на двух составных основаниях, на которых закреплены: ис­точник излучения – ртутная лампа в кожухе 1, коллиматор 2 типа МГТ 2,5*17,5 на стойке и гониометрический столик 5 со зрительной трубой 6, закрепленной на его алидаде.

Рис. 3.27.2.

На кожухе лампы имеется прорезь, в которую устанавливается щель. Исследуемый объект 8 (призма) закреплен в оправе с вклеенными магнитами и устанавливается на основании гониометрического столика. Отсчет углов поворота столика производится по угловой шкале с нониусным отсчетом. Излучение от ртутной лампы, заполняющее щель, преобразу­ется коллиматором в параллель­ный пучок, который направля­ется на призму, установленную на столике гониометра. Откло­ненное излучение наблюдается визуально с помощью зритель­ной трубы, сфокусированной на «бесконечность», что позволяет восстановить изображение ще­ли. Угол отклонения излучения измеряется по отсчетной шкале столика. Отсчет целых градусов производить по шкале лимба против нуля нониуса. К этим данным следует доба­вить количество десятых долей, снятых по шкале нониуса – первое деление нониуса, сов­падающее с каким-либо делением шкалы лимба.

Спектр излучения лампы содержит линии, присущие парам ртути и гелия. Длины волн приведены в Приложении. Визуально наблюдаться могут не все линии.

Порядок выполнения работы

Включите источник света, поверните алидаду гониометра так, чтобы оптическая ось зрительной трубы совпадала с осью коллиматора. При этом в поле зрения окуляра появит­ся изображение входной щели коллиматора.

Проверьте и при необходимости произведите фокусировку коллиматора и зритель­ной трубы в следующей последовательности:

1. Сфокусируйте на оптическом стенде с помощью автоколлиматора трубу на «бесконечность». При отсутствии автоколлиматора можно визуально сфокусировать трубу на удаленный предмет в коридоре или за окном.

2. Установите алидаду гониометра соосно с оптической осью коллиматора. Вращением фокусирующей подвижки коллиматора добейтесь резкого изображения щели.

3. Установите исследуемый объект на предметный столик и проверьте наличие дифра­гировавшего или отклоненного излучения.

Определить преломляющий угол А призмы (в работе используется призма АР-90, у которой в качестве рабочих выбираются две грани под углом 45 °, как показано на рис. 3.27.3). На предметный столик поставить призму так, чтобы биссектриса преломляющего угла призмы примерно совпадала с осью освещенного коллиматора. В этом случае боковые грани призмы работают как зеркала. Сначала невооруженным глазом, а затем с помощью окуляра поймать изображение входной щели освещенного коллиматора по направлению отраженных от боковых граней призмы лучей. Поворачивая окуляр, совместить его нить с изображением щели сначала справа от оптической оси коллиматора, а затем слева. При этом снять отсчеты по лимбу и нониусу гониометра (N₁ и N₂). При таком положении призмы искомый угол А равен:

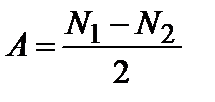. (3.27.8)

Если при перемещении из положения справа в положение слева от оптической оси коллиматора окуляр проходит через ноль лимба, тогда

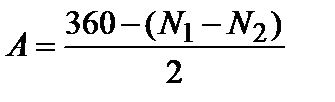. (3.27.9)

Преломляющий угол призмы определить не менее трех раз и найти среднее значение.

Измерить углы наименьшего отклонения для различных длин волн спектра лампы. Прежде всего, необходимо увидеть в окуляр линейчатый спектр лампы. Для этого элемен­ты установки нужно установить в следующем порядке: поместить призму на предметном столике так, как изображено на рис. 3.27.3 (при этом коллиматор, объектив и окуляр образуют угол примерно равный 21-25 градусов).

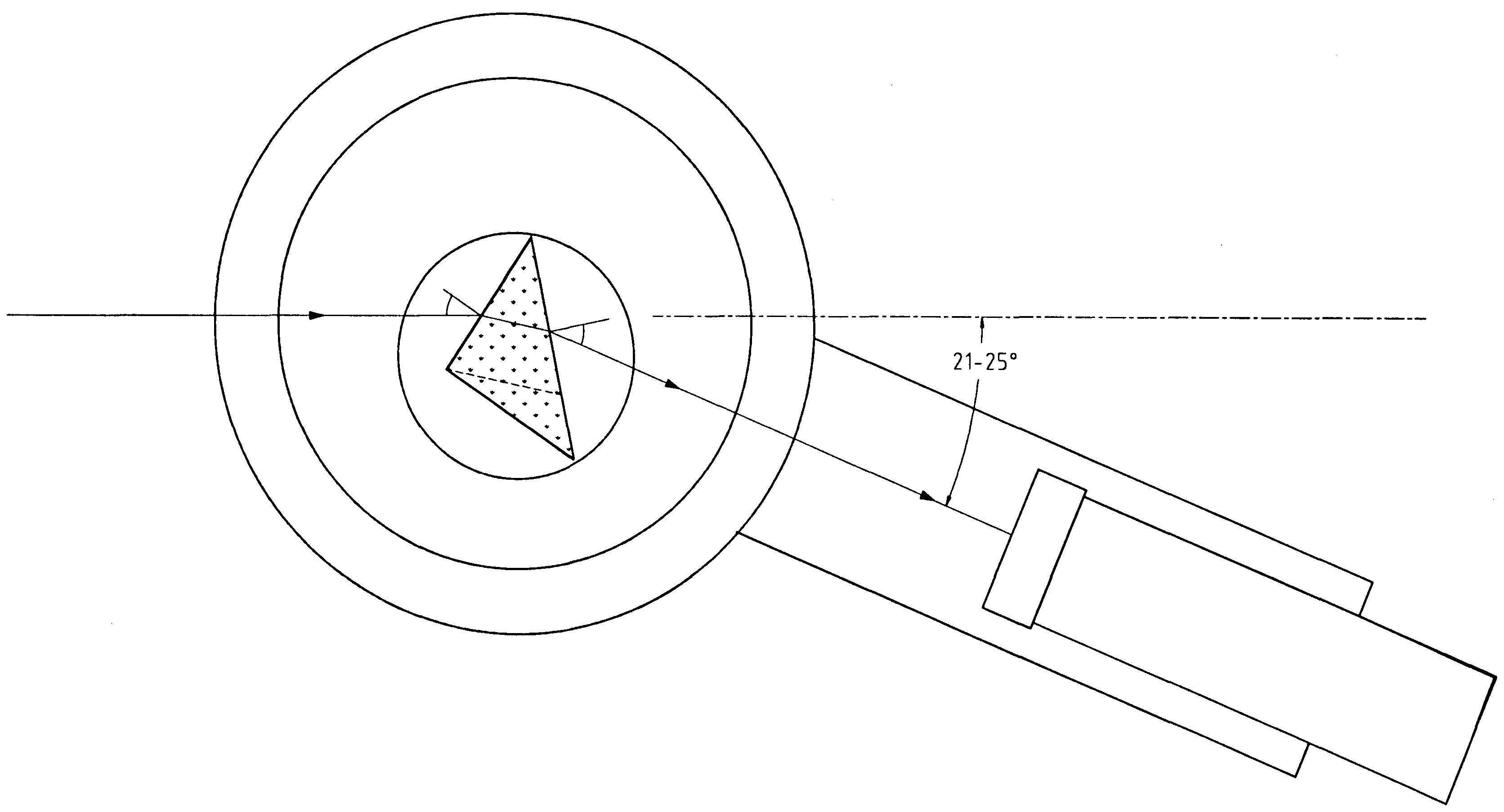
Рис. 3.27.3

Слегка поворачивая столик с призмой и окуляр вблизи данного положения, нужно добиться четкого изображения линий спектра. Далее следует повернуть столик с призмой в одном направлении и проследить за движением спектральных линий. При некотором определенном угле падения луча на призму наблю­даемая спектральная линия останавливается в поле зрения окуляра, а затем начинает дви­гаться в обратном направлении. Положение спектральной линии в момент остановки со­ответствует углу наименьшего отклонения луча δ_min.

Совместив отсчетную нить окуляра с линией спектра в положении минимального отклонения, снять отсчет N₃ по лимбу и нониусу. Далее, чтобы измерить угловую координату лучей, нужно снять призму со столи­ка и совместить окуляр с оптической осью коллиматора, совместить отсчетную нить с изображением входной щели и снять отсчет N₄. Тогда угол наименьшего отклонения для любой спектральной линии:

δ_min = N_{3 –} N₄ . (см. рис. 3.27.1).

Снимать показания не менее 3 раз для всех спектральных линий. Усреднить значения.

Обработка результатов

По измеренным в опыте углам А и δ_min вычислить показатели преломления оптиче­ского стекла призмы для всех указанных длин волн.

Построить график n = n(λ), изображающий дисперсию света в оптическом стекле призмы .

Вывести формулу погрешности для показателя преломления стекла.

Рассчитать дисперсию оптического стекла в желто-зеленой области спектра по формуле

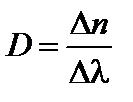. ( 3.27.10)

Контрольные вопросы

1. Что такое дисперсия света?

2. Каков физический смысл показателя преломления света?

3. Как рассчитать показатель преломления призмы?

4. Как определить угол наименьшего отклонения призмы?

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

2. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.

3. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. –560 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.28