Исследование закона малюса и прохождения поляризованного света через фазовую

ПЛАСТИНКУ

Цель работы: проверка закона Малюса и анализ поляризованного света, про­шедшего через фазовую пластинку.

Теоретические положения

Из электромагнитной теории света следует, что световая волна является поперечной, то есть три вектора: напряженность электрического поля Е, напряженность магнитного поля Η и волновой вектор k взаимно перпендикулярны. Свет от обычных источников состоит из множества цугов волн, световой вектор Ε которых ориентирован в поперечной плоскости случайным образом, а колебания различных направлений равновероятны. Такой свет называ­ется естественным или неполяризованным.

Свет, в котором направления колебаний светового вектора упорядочены каким-либо образом, называется поляризованным.Процесс получения поляризованного света называется поляризацией.Если колебания вектора Ε происходят в одной плоскости, то свет считается плоскополяризованным(или линейно поляризованным). Свет, в котором имеется преимуще­ственное направление колебаний вектора Е, называют частично поляризованным.

Плоскость, в которой лежит вектор напряженности электрического поля волны и вол­новой вектор k, называют плоскостью колебанийили плоскостью поляризации.

Поляризация света наблюдается при отражении, преломлении и при прохождении света через анизотропные вещества. Всякий прибор, служащий для получения поляризованного света (независимо от физических эффектов, используемых при этом), называется поляриза­тором.Визуально поляризованный свет нельзя отличить от неполяризованного. Исследова­ние поляризованного света осуществляют с помощью того же прибора, называемого в этом случае анализатором.

Эллиптическая поляризация света

Поляризованное излучение имеет в общем случае эллиптическую поляризацию. При этом ортогональные компоненты светового вектора Е для выбранной системы координат (ось Ζ параллельна направлению распространения света) описываются выражениями вида:

E_x=E_xo sin(ωt + δ_x ), (3.26.1)

Ε_γ=Ε_γο sin(ωt + δ_γ ). (3.26.2)

Сложение ортогональных колебаний вида (3.26.1) и (3.26.2) на плоскости XY дает проекционную картину эллипса. При этом форма эллипса определяется следующими параметрами:

δ = δ_γ – δ_x (3.26.3)

– разность фаз,

tgψ = E_X0 /E_Y0 (3.26.4)

– отношение амплитуд.

При δ, равной нулю или π, эллипс вырождается в прямую и получается линейно поля­ризованный свет. При δ = π/2 и равенстве амплитуд складываемых волн эллипс превраща­ется в окружность – получается свет, поляризованный по кругу.

В зависимости от направления вращения вектора Εразличают правую и левую эллипти­ческую поляризацию. Если по отношению к направлению луча вектор Εвращается по пра­вилу правого винта, поляризация называется правой, в противном случае – левой.

Для описания формы эллипса часто используют другую пару параметров, имеющих бо­лее наглядную геометрическую интерпретацию (рис. 3.26.1):

χ – азимут ориентации большой полуоси эллипса в выбранной системе координат;

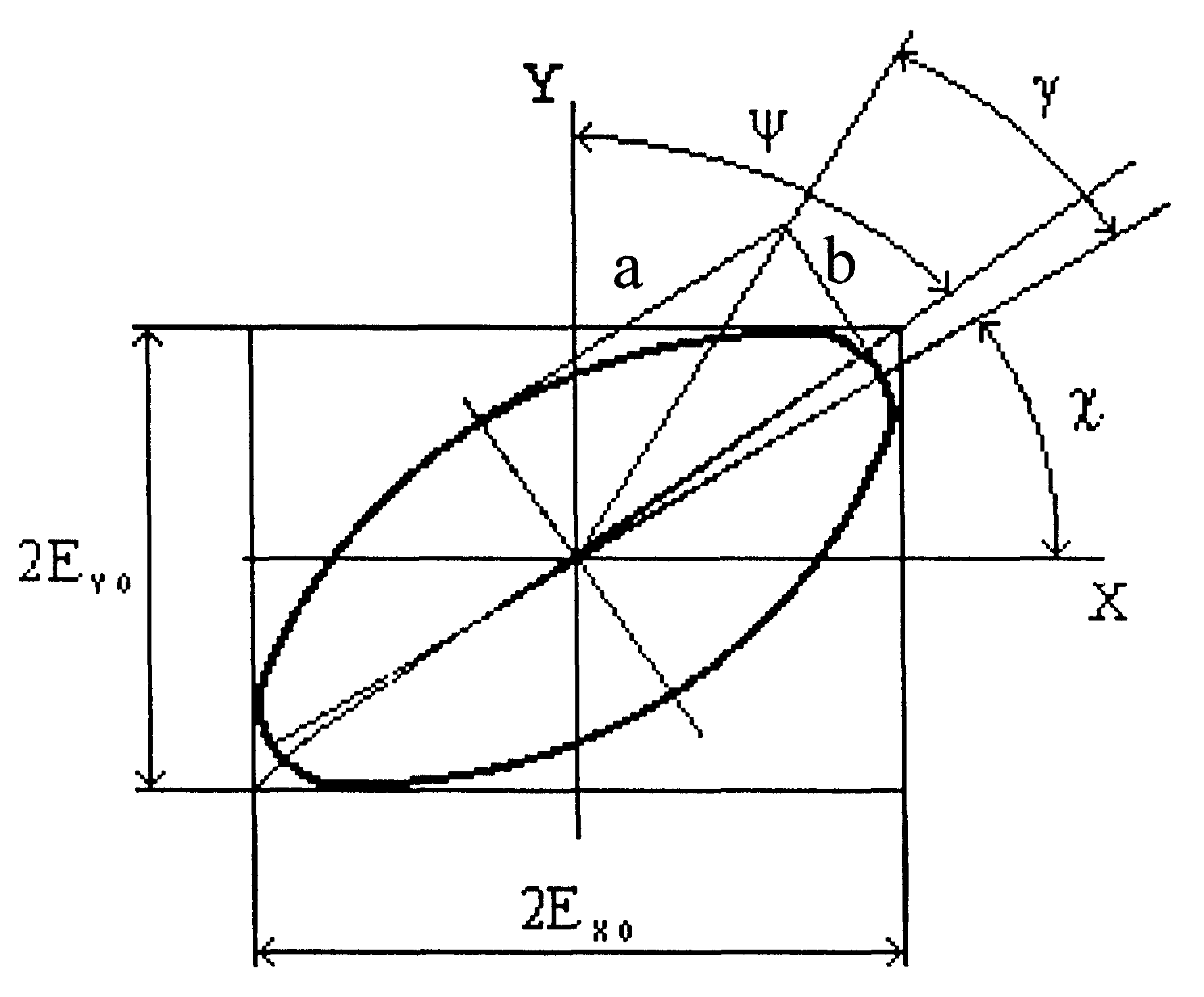
Рис. 3.26.1.

tg γ = b/а – эллиптичность – отношение полуосей эллипса.

Связь между параметрами ψ, δ и χ, γ задается формулами:

cos 2ψ = -cos 2γ cos 2χ, (3.26.5)

tg δ = tg 2γ/sin 2χ, (3.26.6)

tg 2χ = -tg 2ψ cos δ, (3.26.7)

sin 2γ = sin 2ψ sin δ. (3.26.8)

Представление эллипса поляризации двумя парами параметров и соотношение между ними имеют важное практическое значение. Непосредственно измеряемыми параметрами в большинстве измерительных схем являются величины χ и γ, для физической интерпретации результатов измерений часто более удобны параметры ψи δ (например, при построении ма­тематической модели объекта с использованием законов и формул Френеля для обработки результатов измерений).

Закон малюса

Пусть свет на своем пути проходит через поляри­затор и анализатор, причем угол между их плоскостями поляризации составляет φ (рис. 3.26. 2). После поляризатора выйдет свет интенсивностью I₀. Согласно закону Малюса после анализатора мы получим свет, интенсив­ность которого определяется выражением

I = I₀ ^.cos² φ. (3.26.9)

В справедливости этого выражения нетрудно убедиться, вспомнив, что интенсивность пропорцио­нальна квадрату амплитуды Ε.

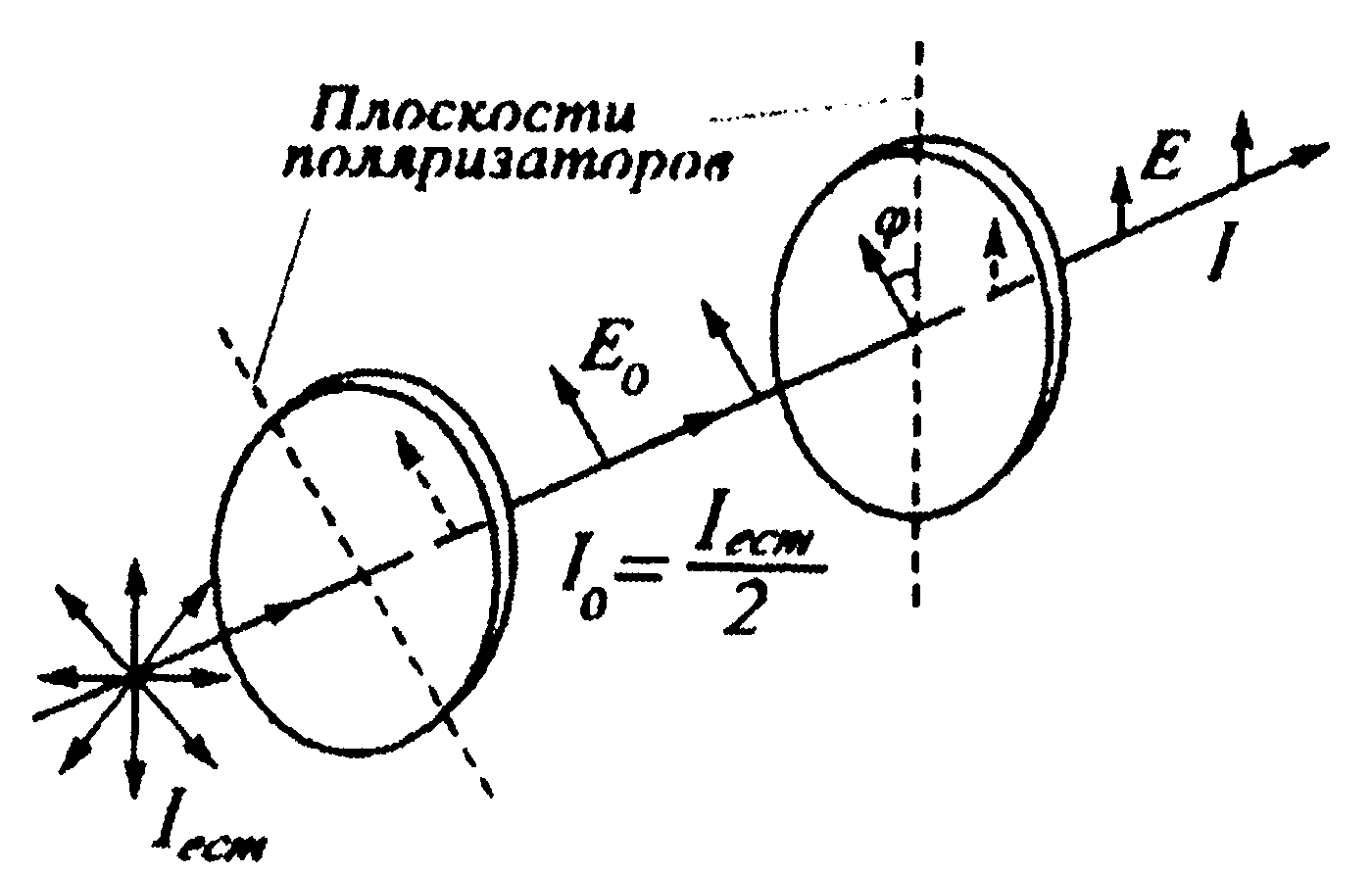
Рис. 3.26.2.

Если частично поляризованный свет пропускать через анализатор, то интенсивность I прошедшего све­та будет меняться в зависимости от положения плоскости поляризации анализатора. Она достигает максимального значения, если плоскость поляризации анализатора и плоскость преимущественных колебаний частично поляризованного света совпадают. Если же эти плоскости перпендикулярны друг другу, то интенсивность света, прошедшего через анализа­тор, будет минимальной.