Определение радиуса кривизны линзы

С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА

Цель работы:изучение интерференции в тонких пленках и определение радиуса кривизны линзы.

Теоретические положения

Интерференция света

Интерференцией света называется явление такого наложения двух, или нескольких волн, в результате которого происходит перераспределение энергии волн, приводящее к усилению интенсивности света в одних местах пространства и уменьшению в других.

Рис. 3.4.1

Из электромагнитной теории Максвелла следует, что свет распространяется в виде электромагнитных волн. Как показал опыт, физиологическое, фотоэлектрическое и др. действия света вызываются колебаниями вектора 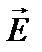напряженности электрического поля волны. Поэтому при характеристике световых колебаний пользуются только вектором .

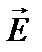Согласно принципу суперпозиции, световые волны, распространяющиеся от разных источников и перекрывающиеся в каком- либо месте пространства, не оказывают влияния друг на друга и напряженность результирующего колебания равна векторной сумме напряженностей складываемых колебаний.

Рассмотрим два гармонических колебания одинаковой частоты, распространяющихся от источников S₁ и S₂ и складывающихся в точке А.

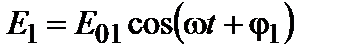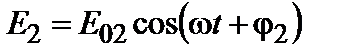; . (3.4.1)

В результате сложения возникает гармоническое колебание с амплитудой

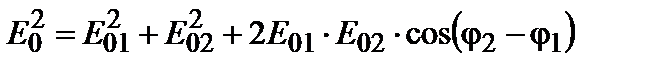. (3.4.2)

Интерференция имеет место, если разность фаз Dj остается постоянной. Такие волны, разность фаз которых в течение времени, достаточного для наблюдения, остается постоянной, называются когерентными. Для когерентности необходимо, чтобы волны были монохроматическими, т.е. имеющими одинаковую строго определенную частоту.

Установлено, что интенсивность света I пропорциональна квадрату амплитуды световой волны:

I ~ 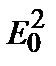. (3.4.3)

При сложении когерентных колебаний интенсивность результирующего колебания, исходя из (3.4.1) и (3.4.2), выразится:

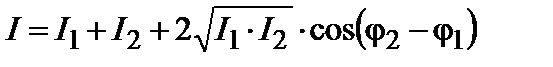, (3.4.4)

то есть результирующая интенсивность отличается от суммы интенсивностей отдельных колебаний: 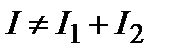. Интерференция обусловлена наличием третьего члена в выражении (3.4.4), который называется интерференционным членом. Он характеризует взаимосвязь складываемых колебаний. Особенно четкой интерференционная картина будет при 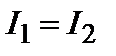. Таким образом, при наложении когерентных колебаний происходит перераспределение энергии светового потока в пространстве, т.е. интерференция света.

Разность расстояний от источников колебаний до рассматриваемой точки экрана 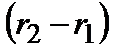называется геометрической разностью хода интерферирующих волн. Величина

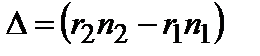(3.4.5)

называется оптической разностью хода интерферирующих волн ( 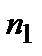и 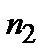- показатели преломления сред, в которых распространяются волны).

Разность фаз и оптическая разность хода интерферирующих волн связаны соотношением:

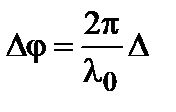. (3.4.6)

Из (3.4.6) следует, что если D равно целому числу длин волн в вакууме:

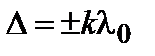,(k=0,1,2,3,...) (3.4.7)

то разность фаз оказывается кратной:

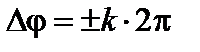. (3.4.8)

Колебания, возбуждаемые в интересующей точке экрана, происходят в одинаковых фазах, и наблюдаются максимумы результирующей интенсивности. Следовательно, (3.4.7) – условие интерференционного максимума.

Если же D равна полуцелому числу длин волн в вакууме

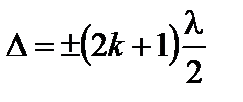, (3.4.9)

,

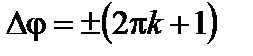то в точках, где разность хода слагаемых волн равна нечетному числу половин длин волн, возникающие колебания происходят в противофазе и наблюдаются минимумы результирующей интенсивности. Условие (3.4.9) – условие интерференционного минимума.

Реальные светящиеся тела испускают некогерентные волны, т.к. поверхность любого светящегося тела состоит из множества атомов, автономно излучающих цуги волн в течение времени 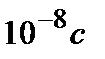, которые не связаны друг с другом фазой и направлением. При этом 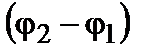непрерывно меняется, принимая с равной вероятностью любые значения. Поэтому среднее значение по времени 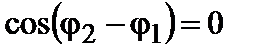, а результирующая интенсивность:

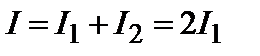, (3.4.10)

т.е. при хаотическом изменении разности фаз происходит простое сложение интенсивностей, и явление интерференции не наблюдается. Только когерентные световые волны могут дать устойчивую во времени интерференционную картину.

Ограничение, налагаемое на интерференцию разностью хода, связано с длиной когерентности. Электромагнитные волны, испускаемые атомами, сохраняют постоянство амплитуды и фазы в течение ограниченного интервала времени, который называется временем когерентности 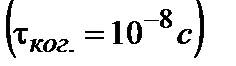. Расстояние

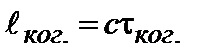, (3.4.11)

Рис. 3.4.2.

на которое распространи­лась волна за время, пока ее фаза и амплитуда оставались в среднем постоянными (~ τ_ког.), на­зывается длиной коге­рентности .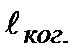

Оказалось, что если 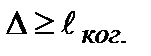, то интерференционный эффект не наблюдается, т.к. при этом соответствующие цуги не наложатся друг на друга вследствие отставания одного из них на расстояние больше 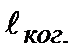. Стационарная контрастная интерференционная картина получается только при соблюдении условия

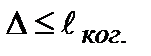, (3.4.12)

называемого условием временной когерентности, которая обусловлена степенью монохроматичности исследуемых колебаний.

Наибольшей когерентностью обладает излучение лазера. Практически когерентные колебания можно получить делением светового пучка путем прохождения и отражения от поверхности (зеркало Френеля, бипризма Френеля, щели Юнга).