Определение показателя преломления стекла

С ПОМОЩЬЮ МИКРОСКОПА

Цель работы:определение показателя преломления стекла с помощью измерения кажущейся толщины стеклянной пластинки.

Теоретические положения

В различных прозрачных средах свет распространяется с различными скоростями, меньшими скорости света в вакууме. Скорость распространения световых волн в среде по теории Максвелла определяется формулой

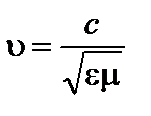, (3.1.1)

где с – скорость света в вакууме, e – диэлектрическая проницаемость среды, m –магнитная проницаемость среды.

Среда, во всех точках которой скорость распространения света одинакова, называется оптически однородной. В такой среде свет распространяется прямолинейно с постоянной скоростью. Если среда неоднородна, то в различных областях скорость света различна, а прямолинейность световых лучей нарушается.

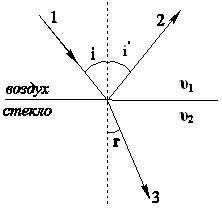
Рис. 3.1.1.

Простейшей неоднородностью является плоская граница раздела двух разнородных сред (например, воздуха и стекла), в которых свет распространяется со скоростями, равными соответственно υ₁ и υ₂. На рис.1 показано, что луч 1, падающий из первой среды под углом i, на границе раздела раздваивается на отраженный луч 2, идущий в той же среде с той же скоростью υ₁, и преломленный луч 3, распространяющийся со скоростью υ₂ во второй среде (в стекле).

Законы отражения света

1. Луч падающий, отраженный и перпендикуляр, восстановленный в точке падения луча к границе раздела двух сред, лежат в одной плоскости.

2. Угол отражения равен углу падения: i^' = i

Законы отражения справедливы при обратном ходе световых лучей, т.е. луч, распространяющийся по пути отраженного, отражается по пути падающего (обратимость хода световых лучей).

Законы преломления света

1. Луч падающий, преломленный и перпендикуляр к границе раздела двух сред, восстановленный в точке падения, лежат в одной плоскости.

2. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред

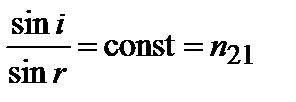. (3.1.2)

Величина n₂₁ называется относительным показателем преломления второй среды относительно первой.

Падающий и преломленный лучи обратимы: если падающий луч пущен по пути преломленного, то преломленный луч пойдет по пути падающего.

Согласно волновой теории, волны от источника света (источника колебаний) распространяются во всех направлениях. Поверхность, до которой одновременно доходят волны от данного источника колебаний, называется волновым фронтом.

Наряду с понятием волнового фронта применяется понятие светового луча. Световые лучи – это семейство прямых, нормальных к волновому фронту.

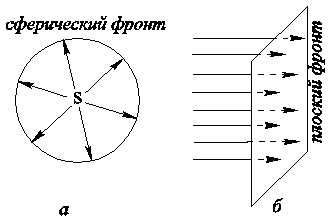
Рис. 3.1.2.

Форма волнового фронта зависит от формы источника колебаний и свойств среды. При точечном источнике S волновой фронт в однородной среде имеет форму сферы; лучи, являющиеся радиусами этой сферы, перпендикулярны волновому фронту (рис.3.1.2 a).

Волны, образующие сферический волновой фронт, называются сферическими. Сферический волновой фронт в изотропной среде является вместе с тем волновой поверхностью, т.е. поверхностью, все точки которой колеблются в одинаковой фазе.

Если фронт волны представляет собой плоскость, то волна называется плоской (рис. 3.1.2 б).

В неоднородной среде, где скорость волны различна в различных направлениях, волновой фронт имеет весьма сложную форму.

В основе волновой теории лежит принцип Гюйгенса:

1. Всякая точка среды, которой достигает волновой фронт, сама становится источником вторичных световых волн.

2. Вторичные волны взаимно гасятся во всех направлениях, кроме направления исходного фронта, поэтому их можно рассматривать как полусферы.

3. Огибающая вторичных сферических волн будет новым фронтом волны.

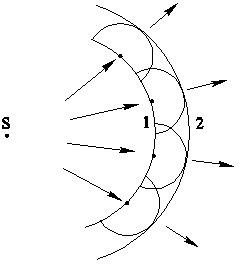
Рис. 3.1.3.

Пусть волновой фронт в однородной среде занимает в данный момент времени положение 1 (рис.3.1.3). Согласно Гюйгенсу, от каждой точки фронта 1 как из центра, начинает распространяться новая сферическая волна. Чтобы построить вторичные волны, вокруг каждой точки исходного фронта опишем сферы радиусом:

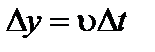, (3.1.3)

где υ –скорость волны, Dt -промежуток времени.

Построив огибающую, получим искомое положение нового волнового фронта 2.

Рассмотрим отражение и преломление света на основе принципа Гюйгенса.

Пусть на границу раздела двух сред с показателями преломления n₁ и n₂ и скоростями распространения света υ₁ и υ₂ соответственно падает фронт плоской волны AB (рис. 3.1.4).

i'

Е

Е

i'

Рис. 3.1.4.

Угол падения лучей равен i. Все точки границы раздела, до которых доходит волновой фронт, становятся по принципу Гюйгенса источниками новых сферических волн. Фронт волны прежде всего достигает точки А на границе раздела. Пока другой край фронта B дойдет до границы раздела сред в точке С, вокруг точки А образуется распространяющийся обратно в первую среду полусферический фронт радиуса:

AD = BC = υ ₁Dt. (3.1.4)

Около промежуточных точек границы раздела возникнут полусферические волны меньшего радиуса. Плоскость СD образует фронт отраженной волны.

Рассмотрим прямоугольные треугольники ABC и АDС. Они имеют общую гипотенузу АС и равные катеты АD = BC. Следовательно, треугольники равны, тогда Ð BAC = Ð DСА. Но Ð BAC равен углу падения, а Ð DСА – углу отражения, т.е. i = i^'_, следовательно, выполняется закон отражения световых волн.

Аналогичным способом выводится закон преломления световых волн при переходе из одной среды в другую. За то время, пока в первой среде край фронта B распространится от точки B до точки С, во второй среде вокруг точки А возникнет вторичная полусферическая волна радиуса AE= υ ₂Dt. От всех остальных точек границы АС (кроме т. С) также распространяются вторичные полусферические волны, радиусы которых окажутся убывающими от точки А к точке С. Тогда касательная плоскость ЕС определит положение фронта преломленных волн.

отношение 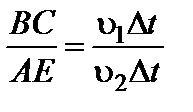. (3.1.5)

Из прямоугольного треугольника АЕС имеем:

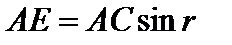, (3.1.6)

где r – угол преломления. Из прямоугольного треугольника АВС имеем:

BC = ACsin i, (3.1.7)

где i − угол падения. Тогда получим:

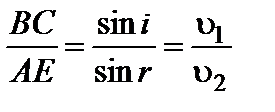. (3.1.8)

Отношение скоростей света для данных двух сред 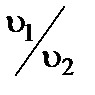величина постоянная. Соотношение (3) выражает закон преломления света.

Сравнивая (3) с (1), получим:

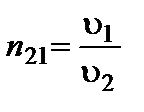. (3.1.9)

Относительным показателем преломления n₂₁ второй среды относительно первой называется отношение скоростей света υ ₁ и υ ₂ соответственно в первой и во второй средах (физический смысл относительного показателя преломления).

Показатель преломления среды относительно вакуума называется абсолютным. Он равен:

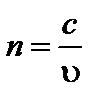, (3.1.10)

где с –скорость света в вакууме, υ – скорость света в среде.

Абсолютный показатель преломления показывает, во сколько раз скорость света в вакууме больше скорости света в данной среде.

Путем простых преобразований относительный показатель преломления можно выразить через абсолютные показатели двух сред:

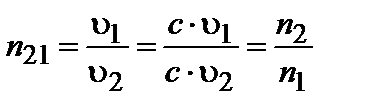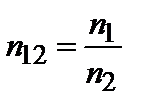, . (3.1.11)

В таблице приводятся абсолютные показатели преломления некоторых веществ

Вещество	Показатель преломления	Вещество	Показатель преломления
воздух вода спирт этил.	1,003 1,333 1,362	стекло (крон) стекло (флинт) алмаз	1,515 1,752 2,420

Для определения показателей преломления веществ существуют различные методы. Одним из них является метод определения показателя преломления стекла с помощью микроскопа.

Содержание работы

В основе метода лежит кажущееся уменьшение толщины пластинки из стекла вследствие преломления световых лучей, проходящих в стекле при рассматривании пластинки нормально к ее поверхности. В точку А, находящуюся на нижней грани пластинки, падает луч света ОА, под углом i к нормали.

Рис. 3.1.5.

Преломившись в точке А, а затем в точке В, он выходит из пластинки под тем же углом i. Наблюдателю кажется, что рассматриваемый луч исходит не из точки А, а из точки D, т.е. толщина пластинки кажется равной СD. Из рис. 3.1.5 видно, что кажущаяся толщина СD = h меньше истинной, т.е. действительной ее толщины АС=H.

Установим связь между показателем преломления стекла n, толщиной стеклянной пластинки H и величиной кажущейся толщины пластинки h.

Показатель преломления стекла относительно воздуха

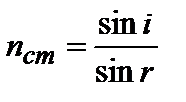. (3.1.12)

Для лучей, близких к нормально падающим, углы падения и преломления малы, тогда синусы можно заменить тангенсами и (6) переписать:

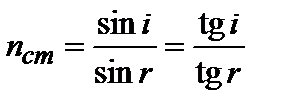. (3.1.13)

Из треугольников AВCи DBC следует

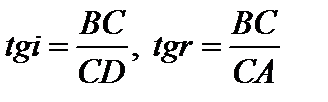. (3.1.14)

Подставив (8) в (7), получим:

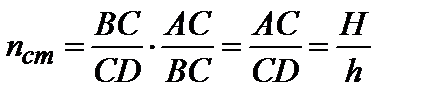или 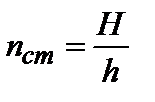(3.1.15)

Т.о., зная толщину пластинки H и ее кажущуюся толщину, можно определить показатель преломления стекла.

ОПИСАНИЕ ОБОРУДОВАНИЯ

Микроскоп с микрометрическим винтом, стеклянные пластинки со штрихами на обеих поверхностях.

Порядок работы

Рис. 3.1.6

Определение кажущейся толщины пластинки производится с помощью микроскопа, снабженного микрометрическим винтом для точного измерения перемещения тубуса.

1. Устанавливают осветительное зеркальце 3 микроскопа так, чтобы поле зрения было хорошо освещено.

1. На предметный столик 1 кладется пластинка 2, на верхней и нижней поверхности которой нанесены параллельные метки, расположенные взаимно перпендикулярно.

2. Сначала микроскоп фокусируется на верхние метки, после чего записывается показание индикатора микрометрического винта. Затем микроскоп фокусируется на нижние метки и записывается новое показание индикатора. Разность показаний индикатора равна кажущейся толщине h.

3. Измеряется при помощи микрометрического винта истинная толщина стекла H.

4. По формуле: 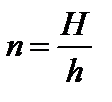вычисляется показатель преломления стекла.

№ п/п	Толщина Н, мм	Перемещение h, мм	Показатель преломления n	Δn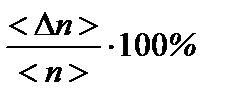
1.
2.
3.
Средн.

Контрольные вопросы

1. Сформулируйте законы преломления и отражения света.

2. В чем состоит принцип Гюйгенса?

3. Выведите законы преломления и отражения света из волновых представлений.

4. В чем состоит физический смысл абсолютного и относительного показателей преломления?

5. Какая рабочая формула используется в работе?

6. Какова методика выполнения работы?

Литература

1. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. –М.: КНОРУС, 2009, 576 с.

2. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.-15-е изд., стереотип. –М.: Издательский центр «Академия», 2007. –560 с.

3. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. –М: Высш. Шк., 1989. –608 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.4