Классическая электродинамика
Здесь состояние электромагнитного поля задается значениями векторов напряженностей Б и Н и индукцией D и В электрических и магнитных полей. Уравнения Максвелла позволяют для этих четырех величин по заданным начальным значениям Б и Н внутри некоторого объема (и граничным условиям) однозначно определить величину электромагнитного поля в любой последующий момент времени.
Понятие состояния в статистических теориях
Статистическая механика
При рассмотрении систем, состоящих из огромного числа частиц (нами рассматривалась молекулярно-кинетиче-ская теория), состояние системы характеризуют не полным набором значений координат и импульсов всех частиц, а вероятностью того, что эти значения лежат внутри определенных интервалов. Тогда состояние системы задается с помощью функции распределения, зависящей от координат, импульсов всех частиц системы и от времени. Функция распределения интерпретируется как плотность вероятности обнаружения той или иной физической величины (например, xt или Pi) в определенных интервалах от хi до xi + + 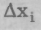 или от Pi до Рi +
или от Pi до Рi + 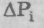 . По известной функции распределения можно найти средние значения любой физиче-
. По известной функции распределения можно найти средние значения любой физиче-
ской величины, зависящей от координат и импульсов, и вероятность того, что эта величина принимает определенное значение в заданных интервалах.
Квантовая механика
В квантовой механике вектором состояния является волновая функция 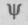 , представляющая собой амплитуду вероятности. Уравнение Шредингера однозначно описывает эволюцию состояния с течением времени. Волновая функция представляет собой, таким образом, полную характеристику состояния: зная волновую функцию
, представляющая собой амплитуду вероятности. Уравнение Шредингера однозначно описывает эволюцию состояния с течением времени. Волновая функция представляет собой, таким образом, полную характеристику состояния: зная волновую функцию 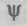 , можно вычислить вероятность обнаружения определенного значения любой физической величины и средние значения всех физических величин. Существует важное различие между описанием состояния в статистической физике и в квантовой механике. Оно состоит в том, что состояние в квантовой механике описывается не плотностью вероятности, а амплитудой вероятности. Плотность вероятности пропорциональна квадрату амплитуды вероятности. Это и приводит к сугубо квантовому эффекту интерференции вероятностей.
, можно вычислить вероятность обнаружения определенного значения любой физической величины и средние значения всех физических величин. Существует важное различие между описанием состояния в статистической физике и в квантовой механике. Оно состоит в том, что состояние в квантовой механике описывается не плотностью вероятности, а амплитудой вероятности. Плотность вероятности пропорциональна квадрату амплитуды вероятности. Это и приводит к сугубо квантовому эффекту интерференции вероятностей.
Как уже отмечалось выше, идеалом классического описания физической реальности считалась динамическая детерминированная форма законов физики. Поэтому первоначально физики негативно относились к введению вероятности в статистические законы. Многие считали, что вероятность в законах свидетельствует о мере нашего незнания. Однако это не так. Статистические законы также выражают необходимые связи в природе. Действительно, во всех фундаментальных статистических теориях состояние представляет собой вероятностную характеристику системы, но уравнения движения по-прежнему однозначно определяют состояние (статистическое распределение) в любой последующий момент времени по заданному распределению в начальный момент. Г.Я. Мякишев подчеркивает, что главное отличие статистических законов от динамических состоит в учете случайного (флуктуаций). В философии давно выработано представление о диалектическом тождестве и различии противоположных сторон любого явления. В диалектике необходимое и случайное — это две противоположности единого явления, две стороны одной медали, которые взаимообусловливают друг друга, взаимопревраща-
ются, не существуют друг без друга. Главное различие между динамическими и статистическими законами с философско-методологической точки зрения состоит в том, что в статистических законах необходимость выступает в диалектической связи со случайностью, а в динамических — как абсолютная противоположность случайного. А отсюда вывод: «Динамические законы представляют собой первый низший этап в процессе познания окружающего нас мира; статистические законы обеспечивают более современное отображение объективных связей в природе: они выражают следующий, более высокий этап познания».
