Основы равновесной термодинамики

Основные формулы

· Молярные теплоёмкости при постоянном объёме ( ) и постоянном давлении ( ):

,

где – число степеней свободы, - универсальная газовая постоянная.

· Связь между удельной ( ) и молярной ( ) теплоёмкостями:

,

где – молярная масса.

· Внутренняя энергия идеального газа:

,

где 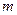- масса газа, - абсолютная температура.

· Изменение внутренней энергии идеального газа:

· Работа расширения газа:

- в общем случае,

где - давление газа, - объём газа.

- при изобарном процессе.

- при изотермическом процессе.

- при адиабатном процессе,

где .

· Первое начало термодинамики:

,

где – количество теплоты, сообщённое системе; - изменение внутренней энергии системы; – работа, совершённая системой против внешних сил.

· Уравнение Пуассона для адиабатного процесса:

.

· Уравнение адиабаты идеального газа в переменных и

.

· Коэффициент полезного действия цикла Карно:

,

где - количество теплоты, полученное от нагревателя; - количество теплоты, переданное холодильнику; - температура нагревателя; - температура холодильника.

Примеры решения задач

Задача 1. Кислород, занимающий при давлении Р=10⁵ Па объем
V = 0,04 м³, расширяется так, что объем увеличивается в два раза. Определите конечное давление и работу, совершенную газом при изобарном, изотермическом и адиабатном процессах.

Дано: Р = 10 5 Па; V = 0,04 м3; V1 =2V =0,08 м3.	Решение: 1. При изобарном процессе Р=const, следовательно, Р1=Р=105 Па. Работа при изобарном процессе А1=РΔV=105 (0,08м3–0,04м3)=0,4·104Дж. 2. При изотермическом процессе начальные и конечные значения давления и объема связаны между собой выражением РV=P2V1, откуда:
P1 - ? P2 - ? P3 - ? A1 - ? A2 - ? A3 - ?

Для определения работы газа при изотермическом процессе воспользуемся выражением: . Из уравнения Клапейрона-Менделеева: , следовательно . После подстановки числовых значений и вычисления получаем: .

3. При адиабатном процессе давление и объем связаны между собой уравнением Пуассона: , где -молярная теплоемкость газа при постоянном давлении, - молярная теплоемкость газа при постоянном объеме. Так как молекула кислорода состоит из двух атомов, то , а отношение Из уравнения Пуассона: . После подстановки и вычисления, получаем: . Работа, совершаемая газом при адиабатном расширении, равна убыли внутренней энергии, т.е. , где Т₃ – абсолютная температура газа после адиабатного расширения. Запишем уравнение состояния до и после адиабатного расширения газа: и , где Т₃ – абсолютная температура газа после адиабатного расширения. Из последних двух уравнений: , а следовательно, . После подстановки числовых значений и вычисления:

Ответ: ; ; ; ; ; .

Контрольные задания

5.1. При изотермическом расширении 2 г азота ( ) при температуре 280 К объём увеличился в два раза. Определите совершённую газом работу, изменение внутренней энергии и количество теплоты, полученное газом.

5.2. Азот ( ) массой 0,1 кг изобарно нагрет от температуры 200 К до температуры 400 К. Определите работу, совершённую газом, полученную им теплоту и изменение внутренней энергии.

5.3. Водород ( ) массой 6,5 г при температуре 300 К и постоянном давлении расширяется вдвое за счет притока тепла извне. Определите работу расширения, изменение внутренней энергии газа и количество теплоты, полученное газом.

5.4. 2 кмоля углекислого газа ( ) нагреваются при постоянном давлении на 50 К. Найдите изменение его внутренней энергии, работу расширения и количество теплоты, полученное газом.

5.5. При адиабатном расширении двух моль кислорода ( ), находящегося при нормальных условиях, объём увеличился в 3 раза. Определите изменение внутренней энергии газа и работу расширения газа.

5.6. Азот ( ), находившийся при температуре 400 К, подвергли адиабатному расширению, в результате которого его объем увеличился в 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.

5.7. Газ расширяется адиабатно и при этом его объём увеличивается вдвое, а температура падает в 1,32 раза. Найдите число степеней свободы этого газа.

5.8. Два моля двухатомного идеального газа нагревают при постоянном объеме до температуры 289 К. Определите количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в 3 раза.

5.9. Работа расширения некоторого двухатомного идеального газа составляет 2 кДж. Определите количество подведенной к газу теплоты, если процесс протекал изобарно.

5.10. Определите количество теплоты, которое надо сообщить кислороду ( ) объёмом 50 л при изохорном нагревании, чтобы давление повысилось на 0,5 МПа.

Электростатика

Основные формулы

· Закон Кулона:

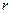где – модуль силы взаимодействия двух точечных зарядов и ; – расстояние между зарядами; - электрическая постоянная; 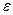-диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума ).

· Напряженность и потенциал электростатического поля:

, , или ,

где 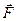– сила, действующая на точечный положительный заряд , помещенный в данную точку поля; – потенциальная энергия заряда ; – работа по перемещению заряда из данной точки поля в бесконечность.

· Напряженность и потенциал электростатического поля, создаваемого точечным зарядом на расстоянии 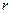от него

; .

· Поток вектора напряженности через площадку :

,

где – вектор, модуль которого равен , а направление совпадает с нормалью к площадке; – составляющая вектора по направлению нормали к площадке.

· Поток вектора напряженности через произвольную поверхность :

.

· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции (наложения) электростатических полей):

; ,

где , – соответственно напряженность и потенциал поля, создаваемого зарядом , – число зарядов, создающих поле.

· Связь между напряженностью и потенциалом электростатического поля:

, или ,

где , , – единичные векторы координатных осей.

· В случае поля, обладающего центральной или осевой симметрией:

.

· Для однородного поля (поля плоского конденсатора):

,

где – разность потенциалов между пластинами конденсатора, – расстояние между ними.

· Электрический момент диполя (дипольный момент):

,

где – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).

· Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, площади и объема:

; ; .

· Теорема Гаусса для электростатического поля в вакууме:

,

где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности ; – число зарядов; – объемная плотность зарядов.

· Напряженность поля, создаваемая равномерно заряженной бесконечной плоскостью:

.

· Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом 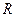с зарядом на расстоянии 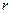от центра сферы:

; при (внутри сферы);

; при (вне сферы).

· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом 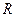на расстоянии 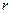от оси цилиндра:

при (внутри цилиндра);

при (вне цилиндра).

· Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1(потенциал ) в точку 2 (потенциал ):

, или ,

где – проекция вектора на направление элементарного перемещения .

· Вектор поляризации диэлектрика:

,

где – объем диэлектрика; – дипольный момент -й молекулы, – число молекул.

· Связь между вектором поляризации и напряженностью электростатического поля в той же точке внутри диэлектрика:

æ _,

где æ – диэлектрическая восприимчивость вещества.

· Связь диэлектрической проницаемости 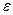с диэлектрической восприимчивостью æ:

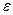= 1 + æ.

· Связь между напряженностью поля в диэлектрике и напряженностью внешнего поля:

.

· Связь между векторами электрического смещения и напряженности электростатического поля:

.

· Связь между векторами , и :

.

· Теорема Гаусса для электростатического поля в диэлектрике:

,

где – алгебраическая сумма заключенных внутри замкнутой поверхности свободных электрических зарядов; – составляющая вектора по направлению нормали к площадке ; – вектор, модуль которого равен , а направление совпадает с нормалью к площадке. Интегрирование ведется по всей поверхности.

· Электроемкость уединенного проводника и конденсатора:

, ,

где – заряд, сообщенный проводнику; – потенциал проводника;
– разность потенциалов между пластинами конденсатора.

· Электроемкость плоского конденсатора:

,

где – площадь пластины конденсатора; – расстояние между пластинами.

· Электроемкость батареи конденсаторов: при последовательном (а) и параллельном (б) соединениях:

а) , б) ,

где – электроемкость -го конденсатора; – число конденсаторов.

· Энергия уединенного заряженного проводника:

.

· Потенциальная энергия системы точечных зарядов:

,

где – потенциал, создаваемый в той точке, где находится заряд , всеми зарядами, кроме -го, - число зарядов.

· Энергия заряженного конденсатора:

,

где – заряд конденсатора; – его электроёмкость; – разность потенциалов между обкладками.

· Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора:

.

· Энергия электростатического поля плоского конденсатора:

,

где – площадь одной пластины; – разность потенциалов между пластинами; – объем области между пластинами конденсатора.

· Объемная плотность энергии электростатического поля:

,

где – напряжённость поля, – электрическое смещение.

Примеры решения задач

Задача 1. Два точечных электрических заряда q₁=1 нКл и q₂=–2 нКл находятся в вакууме на расстоянии d = 10 см друг от друга. Определите напряженность и потенциал поля, создаваемого этими зарядами в
точке А, удаленной от заряда q₁ на расстояние r₁=9 см и от заряда q₂ на расстояние r₂=7 см. Какая сила будет действовать на точечный заряд q΄=1 пКл, если его поместить в точку А?

Дано: q1 = 1 нКл; q2 = -2 нКл; d = 10 см; r1 = 9 см; r2 = 7 см; q΄ = 1 пКл	Решение: Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Рис.6.1 Напряженность электрического поля в искомой точке будет равна геометрической сумме напряженностей и полей, создаваемых каждым зарядом в отдельности:
Е = ? =? F = ?

Модуль вектора найдем по теореме косинусов (рис.6.1):

(1)

где – угол между векторами ₁ и ₂, который может быть найден из треугольника со сторонами r₁, r₂ и d: . В данном случае во избежание громоздких записей удобно значение вычислить отдельно:

Напряженность электрических полей, создаваемых соответственно зарядами q₁ и q₂:

(2)

Подставляя выражения для Е₁ и Е₂ из (2) в (1) и вынося общий множитель 1/(4 ) за знак корня, получаем:

(3)

Сила, действующая на заряд q΄:

F = q΄E. (4)

В соответствии с принципом суперпозиции электростатических полей потенциал результирующего поля, создаваемого двумя зарядами q₁ и q₂ , равен алгебраической сумме потенциалов, т.е.

= ₁ + ₂ . (5)

Потенциал поля точечного заряда q на расстоянии r от него выражается формулой:

(6)

В нашем случае согласно формулам (5) и (6) получаем:

(7)

Подставив в формулы (3), (4) и (7) численные значения физических величин, произведем вычисления:

Ответ: ; .

Контрольные задания

6.1. Расстояние между одноименными одинаковыми зарядами
q = 2 нКл равно 10 см. Определите напряженность поля, создаваемого этими зарядами в точке, находящейся на расстоянии 8 см от первого и 6 см от второго заряда.

6.2. Расстояние между двумя точечными зарядами
q₁= 2 нКл и q₂ = – 3 нКл, расположенными в вакууме, равно
25 см. Определите напряженность поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние 20 см и от второго заряда на 15 см.

6.3. Расстояние между одноименными одинаковыми зарядами q = 2 нКл равно 10 см. Определите напряженность поля, создаваемого этими зарядами в точке, находящейся на расстоянии 8 см от первого и 6 см от второго заряда.

6.4. Расстояние между двумя точечными зарядами
q₁= 2 нКл и q₂ = – 3 нКл, расположенными в вакууме, равно
25 см. Определите напряженность поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние 20 см и от второго заряда на 15 см.

6.5. Определите напряженность поля в точке, находящейся на прямой, соединяющей заряды q₁ =10 нКл и q₂ =-8 нКл, на расстоянии 8 см справа от отрицательного заряда. Расстояние между зарядами равно 20 см.

6.6. С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости? Поверхностная плотность заряда на каждой плоскости 2 мкКл/м².

6.7. К бесконечно заряженной плоскости с поверхностной плотностью заряда 8,85 нКл/см² прикреплен на нити одноименно заряженный шарик с массой 1г и зарядом 2нКл. Какой угол с плоскостью образует нить, на которой висит шарик?

6.8. Два шарика массой 1 кг каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на
угол 60˚?

6.9. Два шарика одинакового радиуса и массы подвешены на двух нитях так, что их поверхности соприкасаются. После сообщения шарикам заряда 4^.10^-7Кл они оттолкнулись друг от друга и разошлись на угол 60˚. Найдите массу каждого шарика, если длина нити 20 см.

6.10. Четыре одинаковых точечных заряда q₁ =q₂ = q₃ = q₄ = 2 нКл находятся в вершинах квадрата со стороной 10 см. Определите силу, действующую на один из зарядов со стороны трех других.

6.11. Расстояние между пластинами плоского конденсатора 5 мм. После зарядки конденсатора до разности потенциалов 500 В между пластинами конденсатора поместили стеклянную пластинку (e=7), полностью заполняющую пространство конденсатора. Определите: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластинке.

6.12. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика — слюдяной пластиной (e₁=7) толщиной d₁ = 1 мм и парафиновой пластиной (e₂=2) толщиной d₂ = 0,5 мм. Определите: 1) напряженности электростатических полей в слоях диэлектрика; 2) электрическое смещение, если разность потенциалов между пластинами конденсатора U = 500 В.

6.13. Расстояние между пластинами плоского конденсатора d = 5 мм, разность потенциалов U = 1,2 кВ. Определите: 1) поверхностную плотность заряда на пластинах конденсатора; 2) поверхностную плотность связанных зарядов на диэлектрике, если известно, что диэлектрическая восприимчивость диэлектрика, заполняющего пространство между пластинами, æ = 1.

6.14. Пространство между пластинами плоского конденсатора заполнено стеклом (e=7). Расстояние между пластинами
d = 5 мм, разность потенциалов U = 1 кВ. Определите:
1) напряженность поля в стекле; 2) поверх­ностную плотность заряда на пластинах конденсатора; 3) поверхностную плотность связанных зарядов на стекле.

6.15. К пластинам плоского воздушного конденсатора приложена разность потенциалов U₁ = 500 В. Площадь пластин
S = 200 см², расстояние между ними d = 1,5 мм. После отключения конденсатора от источника напряжения пространство между пластинами заполнили парафином (e = 2). Определите разность потенциалов U₂ между пластинами после внесения диэлектрика. Определите также электроемкости конденсатора C₁ и С₂ до и после внесения диэлектрика.

6.16. К пластинам плоского воздушного конденсатора приложена разность потенциалов U₁ = 500 В. Площадь пластин
S = 200 см², расстояние между ними d = 1,5 мм. При включенном источнике питания в пространство между пластинами конденсатора внесли парафин (e = 2). Определите разность потенциалов U₂ между пластинами после внесения диэлектрика. Определите также электроемкости конденсатора C₁ и С₂ до и после внесения диэлектрика.

6.17. Плоский воздушный конденсатор электроемкостью
С = 10 пФ заряжен до разности потенциалов U₁ = 500 В. После отключения конденсатора от источника тока расстояние между пластинами конденсатора было увеличено в 3 раза. Определите: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин.

6.18. К пластинам плоского воздушного конденсатора приложено напряжение U₁ = 500 В. Площадь пластин S = 200 см², расстояние между ними d₁ = 1,5 мм. Пластины раздвинули до расстояния d₂ = 15 мм. Найдите энергии W₁ и W₂ конденсатора до и после раздвижения пластин, если источник тока перед раздвижением отключался.

6.19. К пластинам плоского воздушного конденсатора приложено напряжение U₁ = 500 В. Площадь пластин S = 200 см², расстояние между ними d₁ = 1,5 мм. Пластины раздвинули до расстояния d₂ = 15 мм. Найдите энергии W₁ и W₂ конденсатора до и после раздвижения пластин, если источник тока перед раздвижением не отключался.

6.20. Электроемкость батареи, образованной двумя последовательно соединенными конденсаторами, равна 100 пФ, а заряд батареи 20 нКл. Определите электроемкость второго конденсатора, а также разности потенциалов на обкладках каждого конденсатора, если электроемкость первого конденсатора 200 пФ.