А.а. барунин, д.с. маслобоев

А.А. БАРУНИН, Д.С. МАСЛОБОЕВ

ТЕРМОДИНАМИЧЕСКИЕ

РАСЧЕТЫ

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет «Военмех»

А.А. БАРУНИН, Д.С. МАСЛОБОЕВ

ТЕРМОДИНАМИЧЕСКИЕ РАСЧЕТЫ

Учебное пособие

Санкт-Петербург

УДК 541(075.8)

Б26

Барунин, А.А. Термодинамические расчеты: учебное пособие / А.А. Барунин, Д.С. Маслобоев; Балт. гос. техн. ун-т. – СПб., 2016. – 24 с. ISBN 978-5-85546-923-3   Излагаются в упрощенной форме краткие теоретические сведения по одной из основных тем курса химии – «Химическая термодинамика», а также методы и примеры решения типовых задач по расчету термодинамических характеристик химических реакций. Предназначено для студентов технических специальностей, изучающих дисциплину «Химия». Может быть использовано студентами при подготовке к зачету или экзамену.

Б26

УДК 541(075.8)

Р е ц е н з е н т канд. хим. наук, начальник отдела физико-хими-ческих методов исследования АО «ЦНИИМ» В.Н. Разуваев

Утверждено

редакционно-издательским

советом университета

ISBN 978-5-85546-923-3© Авторы, 2016

© БГТУ, 2016

ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ

Энергия

При рассмотрении закономерностей протекания химических процессов наиболее важными являются два типа закономерностей: энергетические и временные. Первые изучает химическая термодинамика, вторые – химическая кинетика.

Изначально термодинамика – это наука о «движении тепла». Она возникла в начале XIX века как теоретическая база создания тепловых машин (в основном паровых котлов), послуживших основой промышленной революции.

Термодинамическое описание химических процессов включает в себя решение двух задач:

1) изучение энергетических характеристик термодинамических систем;

2) возможность предсказать направление протекания самопроизвольных химических процессов и указать способы осуществления целенаправленных химических превращений.

Энергия – одно из основных физических понятий и потому не имеет исчерпывающего определения. Для наших целей примем, что энергия – это такая характеристика движения и взаимодействия тел, которая связана с их способностью совершать изменения в состоянии системы и внешней среды.

Видов энергии очень много: механическая, тепловая, электромагнитная, ядерная и т.д. Каждая из них может только видоизменяться, т.е. превращаться в другие виды энергии.

Термодинамическая система – это ограниченная область пространства, занятая ее элементами. Элементы системы (подсистемы) считаются однородными. Граница системы может быть и физической (стенки сосуда), и мысленной. Все, что вне системы, составляет окружающую среду.

Термодинамические системы бывают трех видов:

1) изолированные (нет обмена ни веществом, ни энергией с окружающей средой). Примеры – герметичный сосуд с газом с теплоизоляционной оболочкой, Вселенная в целом;

2) замкнутые (нет обмена веществом с окружающей средой). Пример – герметичный сосуд;

3) открытые (есть и энерго- и массообмен с окружающей средой). Примеры – костер, человек.

В химической термодинамике изучаются только изолированные и замкнутые системы.

Состояния систем характеризуются параметрами состояния(функциями процесса) и функциями состояния.

Параметры состояния системы – это свойства, однозначно характеризующие однородные части системы. Например, для идеального газа параметрами являются четыре свойства: давление р, объём V, температура T и количество молей ν. Любые три из них независимы. Это означает, что, задав произвольно любые три из четырех параметров, мы по уравнению состояния (в данном случае это будет уравнение состояния Клапейрона–Менделеева) найдем четвертый:

рV= ν RT.

Для более сложных систем могут появиться дополнительные параметры состояния, например химический состав.

Остановимся на параметре T. Это абсолютная температура в градусах Кельвина, которая всегда положительна. Она характеризует среднюю кинетическую энергию хаотического движения, приходящуюся на одну степень свободы частицы системы:

<E> =1/2 ikT,

где i – число степеней свободы, k – постоянная Больцмана, <E> – средняя кинетическая энергия хаотического движения; i=3 для одноатомных молекул (три направления свободного движения), i=5 для двухатомных (свободное движение плюс два вращения), i=6 для трехатомных и более (свободное движение плюс три вращения).

С точки зрения термодинамики температура – особый параметр. Она является индикатором направления передачи тепла: самопроизвольно тепло передается от более горячего тела к более холодному.

Существует понятие нулевого (или четвертого) закона термодинамики, который гласит: две системы, находящиеся в тепловом равновесии с третьей, находятся в равновесии и друг с другом. При этом все три системы характеризуются одинаковым значением определяющего это равенство параметра – температуры. Этот закон сформулировал Ральф Говард Фаулер в 1931 г.

Параметры термодинамической системы делятся на интенсивные и экстенсивные. Интенсивные параметры не зависят от количества вещества в системе (давление, температура, напряженность электрического поля и др.), а экстенсивные зависят (объем, масса, заряд и др.).

Параметры состояния связаны друг с другом функциональными зависимостями. Те из функций, которые не зависят от истории системы, т.е. от того, как она попала в данное состояние, называются функциями состояния. Они однозначно характеризуют это состояние.

В качестве примера приведём такую функцию состояния системы как внутренняя энергия U. К термодинамическому пониманию этой величины мы вернемся позже, пока же достаточно того, что мы знаем об энергии: в изолированных системах она сохраняется во времени.

Особую форму в термодинамике имеет время. Оно лишено такого качества, как длительность, и проявляется только как фиксация качественных изменений. В термодинамике рассматривается не ход процесса, а только его результат. Результатом же в классической термодинамике всегда является равновесное состояние системы и среды. Равновесное состояние характеризуется неизменностью параметров во времени. Термодинамический процесс – это переход системы из одного равновесного состояния в другое. Событие в термодинамике – это изменение равновесных параметров в ходе термодинамического процесса.

По разным признакам в термодинамике процессы классифицируются так:

1. По конечному результату – например, циклические,в результате которых параметры приобретают исходные значения.

2. По характеру взаимодействия с окружающей средой – обратимые и необратимые. Обратимые процессы не оставляют изменений в окружающей среде.

3. По местонахождению причины – самопроизвольные (причина в самой системе) и вынужденные (причина в окружающей среде).

4. При постоянстве какого-либо параметра процесса – изотермический (при постоянной температуре), изобарический, или изобарный (при постоянном давлении), изохорический, или изохорный (при постоянном объеме), адиабатический, или адиабатный (без обмена энергией с окружающей средой), самопроизвольный, несамопроизвольный, неравновесный, равновесный, обратимый, необратимый.

Термодинамика строится на трёх законах (постулатах, началах): первом, втором и третьем. Иногда говорят и о нулевом (или четвертом) законе термодинамики.

Тепловой эффект реакции

Тепловым эффектом химической реакции называется количество теплоты, выделяющейся в экзотермических процессах или поглощающейся в эндотермических процессах при осуществлении реакции при постоянном давлении или постоянном объёме и равенстве температур начального и конечного состояний системы.

Изучением тепловых эффектов реакций занимается термохимия. Наиболее распространенным является метод работы и расчётов при постоянном давлении.

В отличие от химической термодинамики в термохимии процессы рассматриваются с точки зрения окружающей среды, а потому знаки тепловых эффектов обратные: «+» для экзотермических и
«-» для эндотермических процессов. Иными словами,

Q_х.р= - ∆ H_х.р (или Q_r = - ∆H_r).

Индекс «х.р» – химическая реакция, «r» – reaction (реакция).

При записи стехиометрических уравнений в термохимии обязательно указывается агрегатное состояние реагентов и продуктов реакции, а также тепловой эффект:

2H₂O_ж + 2Na_тв = 2NaOHр-р + H_2г + Q_х.р (- ∆H_х.р).

В термохимии введено важное понятие теплоты образованияхимического соединения: это удельный тепловой эффект реакции образования сложного химического соединения из чистых простыхвеществ, находящихся в равновесном состоянии при стандартных условиях. Удельный – значит приходящийся на 1 моль вещества. Стандартные условия давление 1,013∙10⁵ Па (1 атм) и фиксированная температура (298,15 К).

Из определения следует, что теплота образования чистых простых веществ равна нулю. Например, для реакции C_графит + O_2г =
= CO₂ + Q_х.р,проведенной в стандартных условиях, Q_х.р = Q_{обр. CO2}.

В результате большого объёма экспериментальных исследований составлены таблицы теплот образования для огромного количества веществ. Они представлены в виде стандартных энтальпий образования, имеющих вид: ∆_fH⁰_298A, где индекс «f» означает formation (образование), индекс «0» – стандартное состояние, 298 – температуру,
A – вещество. Последний индекс часто опускают, вынося указание на формулу вещества в шапку таблицы.

Величина ∆_fH⁰₂₉₈ имеет размерность кДж/моль и относится к образованию одного моляданного вещества А.

Понятие энтропии

Чтобы это понять, рассмотрим ещё одну функцию состояния, которую ввел в термодинамику Р. Клаузиус (1850 г.) при анализе КПД тепловой машины.

Оказалось, что для обратимых тепловых процессов, протекающих при постоянной температуре, изменение некоторой величины S связано с количеством энергии, передаваемой в форме тепла ∆Q_T, следующим соотношением:

∆S = ∆Q_T /T.

Величина S является функцией состояния, поскольку, как оказалось, зависит только от природы и параметров системы T, р и V и не зависит от того, каким путем система приходит из начального состояние в конечное. Эта функция имеет размерность Дж/ К и называется энтропией.

В пределе соотношение, введенное Клаузиусом (и называемое формулой Клаузиуса) выглядит так:

dS = δ Q_T / T.

Формула Клаузиуса является определением термодинамической энтропии как функции состояния.

Энтропия – экстенсивная функция состояния, поэтому для удобства сравнения различных систем (а в химии системы различаются по составу) чаще используется удельная характеристика – энтропия одного моля вещества в системе, имеющая размерность Дж/(моль К).

Обратим внимание на то, что в правой части формулы Клаузиуса – строго фиксированная температура (температура – мера кинетической энергии частиц). А потому передаваемое здесь тепло не изменяет среднюю кинетическую энергию частиц в системе. Но что же тогда меняется?

Поскольку тепло – это та часть кинетической энергии частиц системы, которая связана исключительно с хаотическим движением,можно сказать, что понятие тепла выявляетособую качественную характеристику системы – её хаотичность, а энтропия – количественная мера хаотичности системы.

Осознание понятия термодинамической энтропии, количественно характеризующей хаос, утвердило и сам хаос как одно из объективных качеств окружающего нас физического мира,равнозначное таким его характеристикам, как энергия, масса, объем, давление.

К таким же выводам приводит и другой подход к определению энтропии, который развил Л. Больцман, исходя из вероятностного подхода к описанию термодинамических систем.

Больцман связал хаотичность с непредсказуемостью: чем более хаотична система, тем труднее предсказать ее конкретную структуру при заданном термодинамическом состоянии, т.е. при заданных параметрах. Например, для газов чрезвычайно сложно указать конкретные координаты и импульсы всех молекул в заданном объеме при определенных р, V, T. Он ввел и меру сложности предсказания – термодинамическую вероятность W.

Термодинамическая вероятность W – это число возможных микросостояний системы, которые обеспечивают параметры данного макросостояния.

Больцман показал, что такая, вероятностная, трактовка хаотичности связана с энтропией по Клаузиусу соотношением

S = k∙lnW,

где k – постоянная Больцмана (1,38∙10^{- 23}Дж/К), W – термодинамическая вероятность данного состояния.

Рассмотрим такой вопрос: сколькими способами (взаимным расположением в пространстве и заданием энергетического состояния) можно реализовать систему, содержащую 1 моль газообразного водорода при давлении 1,013∙10⁵ Па и температуре 298 К?

Энтропия моля водорода при этих (стандартных) условиях равна S⁰_{298 H2} = 130,59 Дж/(моль К).

Расчет по формуле Больцмана дает

W 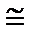exp (10000000000000000000000000).

Таково число вариантов размещения в 22,4 литрах пространства 6,02∙10²³ штук молекул водорода при стандартных условиях. Очевидно, что это «стандартное состояние» весьма хаотично!

Расчет изменения энтропии в конкретных процессах является хорошо разработанным разделом термодинамики. После введения понятия энтропии оказалось, что в термодинамических системах, помимо первого, существует и действует второй закон (второе начало) термодинамики.

Он имеет много формулировок, первую из которых дал Клаузиус (теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому), однако для нас будет важна следующая:
в изолированных системах самопроизвольно протекают только процессы, сопровождающиеся увеличением энтропии.

Математически это записывается как

dS_ad≥0 (здесь индекс ad – адиабатический процесс).

Равенство нулю dS_ad возможно при обратимом проведении циклических (равновесных) процессов.

Следует подчеркнуть, что действие второго начала термодинамики строго ограничено только изолированными системами. А вот понятие энтропии, которое породило этот закон, применимо ко всем видам термодинамических систем и играет важную роль в понимании хода всех термодинамических процессов. Вне рамок адиабатических процессов энтропия, по физическому смыслу представляющая хаос, если в системе ей не противостоит какая-то противодействующая причина, стремится к возрастанию.

В общем случае для любого процесса второй закон термодинамики можно представить в виде

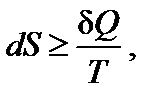
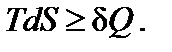
Знак равенства относится к равновесным процессам, знак неравенства – к неравновесным. Знак неравенства появляется потому, что работа, производимая системой в необратимом (неравновесном)
процессе, меньше работы, производимой в обратимом (равновес-
ном) процессе: W_неравн< W_равн. Из первого начала термодинамики
(dU =dQ + dW) и с учетом того, что внутренняя энергия – функция состояния (dU_равн = dU_неравн), следует: dQ_неравн > dQ_равн. Тогда для необратимого (неравновесого) процесса изменение энтропии

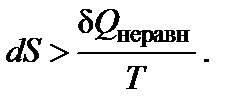
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Пример 1. Определить тепловой эффект процесса термического разложения хлорида аммония и составить термохимическое уравнение реакции.

Решение. Реакция выражается уравнением NH₄Cl(к) → NH₃(г) + + HCl(г). Согласно следствию из закона Гесса

∆H⁰_{298 (реакции)} = ∑(n'∆_fH⁰₂₉₈)_прод− ∑(n''∆_fH⁰₂₉₈)_исх =

= ∆H⁰₂₉₈(NH₃)(г) + ∆H⁰₂₉₈(HCl)(г) - ∆H⁰₂₉₈(NH₄Cl)(к).

Используя справочные данные значений ∆H⁰₂₉₈веществ, получаем

∆H⁰_{298(реакции)} = (-46,2 – 92,2) – (-314,2) = + 175 кДж.

Таким образом, термическое разложение NH₄Cl является эндотермической реакцией. Термохимическое уравнение имеет вид

NH₄Cl(к) → NH₃(г) + HCl(г) - 175 кДж.

Пример 2. Тепловой эффект реакции С(т) + ½О₂(г) = СО(г) при постоянном объеме и температуре 20º С равен 108,9 кДж. Определить тепловой эффект реакции при постоянном давлении.

Решение. Соотношение между тепловым эффектом при
V = const (Q_V =∆U) и тепловым эффектом при р = const (Q_р =∆H) выражается уравнением ∆H = ∆U + р∆V. Определяем изменение числа молей газов в ходе реакции:

∆n = 1 - ½ = ½ (моль).

Учитывая значение Т = 293 К, R = 8,314 Дж/моль·К, а также единицы измерения величин, получаем для теплового эффекта реакции при р = const

∆H = ∆U + ∆n R T = - 108,9+1/2·8,314 /10³·293 = - 107,68 кДж.

Пример 3. Возможен ли процесс получения металлического железа из оксида Fe₂O₃ действием водорода при стандартных условиях Fe₂O₃(к) + 3H₂(г) = 2Fe(к) + 3H₂O(ж)? Как скажется повышение температуры на вероятности протекания этой реакции?

Решение. Для ответа на первый вопрос задачи необходимо
рассчитать изменение свободной энергии Гиббса ∆G⁰₂₉₈ для
рассматриваемой реакции, используя уравнение ∆G_{T(реакции)} =
= ∆H_{T (реакции)} − T∆S_{Т(реакции)}. Значения ∆H⁰₂₉₈ и ∆S⁰₂₉₈ для всех веществ, участвующих в реакции, приводятся в задании или берутся из таблиц термодинамических величин.

По следствию из закона Гесса ∆H⁰_{298(реакции)} =
= ∑(n'∆_fH⁰₂₉₈)_прод − ∑(n''∆_fH⁰₂₉₈)_исх,найдем

∆H⁰_{298(реакции)} = 3∆H⁰₂₉₈ (H₂O)(ж) – ∆H⁰₂₉₈(Fe₂O₃)(к) = 3 (-285,8) – (-822,0)=

= - 857,4 + 822,0 = - 35,4 кДж.

Значение ∆H⁰₂₉₈ (H₂)(г) = 0 и ∆H⁰₂₉₈ (Fe)(к) = 0.

Согласно

∆S⁰_{298(реакции)}= ∑(n'S⁰₂₉₈)_прод − ∑(n''S⁰₂₉₈)_исх,

найдем

∆S⁰_{298(реакц)} =[3S⁰₂₉₈(H₂O)(ж) + 2S⁰₂₉₈(Fe)(к)] - [S⁰₂₉₈ (Fe₂O₃)(к) +

+ 3S⁰₂₉₈(H₂)(г)] = (3·70,1 + 2·2,27) - (87,0 + 3·130,5) = - 213,8 Дж/К.

По найденным данным вычисляем

∆G⁰₂₉₈ = ∆H⁰₂₉₈ − T∆S⁰₂₉₈ = - 35,4 + 213,8·10^-3·298 = 28,34 кДж.

Положительное значение ∆G указывает на невозможность восстановления Fe₂O₃ водородом при стандартных условиях.

Ответ на второй вопрос задачи определяется знаком ∆S. Рас-
чет показал, что ∆S⁰_{298реакции} < 0, следовательно, в уравнении ∆G = ∆H − T∆S величина −T∆S > 0. Повышение температуры приводит к увеличению значения ∆G, а значит, не будет способствовать протеканию реакции в прямом направлении.

Пример 4. Определить стандартный тепловой эффект реакции, если известны теплоты образования веществ.

1. Реакция образования сульфата алюминия из оксида алюминия и триоксида серы:

Al₂O_{3 (кр)} + 3SO_{3 (газ)} = Al₂(SO₄)_{3 (кр)}.

Вещество	Al2O3 (кр)	SO3 (газ)	Al2(SO4)3 (кр)
DfН0298, кДж/моль	–1676,1	–395,9	–3442,8

Решение. Тепловой эффект реакции определяем по первому следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈=(1×D_fН⁰_Al2(SO4)3)–(1×D_fН⁰_Al2O3 + 3×D_fН⁰_SO3 ) =

=1 (–3442,8) – [1 (–1676,1) + 3(–395,9)] = –579 [кДж].

2. Реакция взаимодействия метана и диоксида углерода с образованием оксида углерода и водорода:

CH_{4 (газ)} + CO_{2 (газ)} = 2 CO _(газ) + 2H_{2 (газ)}.

Вещество	CH4 (газ)	CO2 (газ)	CO (газ)	H2 (газ)
DfН0298, кДж/моль	–74,85	–393,51	–110,5

Решение. Тепловой эффект реакции определяем по следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈=(2×D_fН⁰_CO + 2×D_fН⁰_H2)–(1 D_fН⁰_CH4 + 1 D_fН⁰_CO2) =

=[2 (–110,5) + 2×0] – [1 (–74,85) + 1 (–393,51)] = 247,36 [кДж].

Пример 5. Определить стандартный тепловой эффект реакции, если известны стандартные теплоты сгорания веществ. Реакция взаимодействия уксусной кислоты и этилового спирта с образованием сложного эфира – этилацетата:

CH₃COOH_(ж) + C₂H₅OH_(ж) = CH₃COOC₂H_5(ж) + H₂О_(ж).

Вещество	CH3COOH(ж)	C2H5OH(ж)	CH3COOC2H5(ж)	H2О(ж)
DcН0298, кДж/моль	–873,79	–1366,91	–2254,21

Решение. Тепловой эффект реакции определяем по следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈ =(1 D_cН⁰_ук + 1 D_cН⁰_эс)–(1 D_cН⁰_эа + 1 D_cН⁰_H2O) =

= [1 (–873,79) +1 (–1366,91)] – [1 (–2254,21)+ 1×0] = 13,51[кДж].

Пример 6. Определить изменение энтропии в стандартных условиях при протекании реакции:

CH_{4 (газ)} + CO_{2 (газ)} = 2CO _(газ) + 2H_{2 (газ)}.

Вещество	CH4 (газ)	CO2 (газ)	CO (газ)	2H2 (газ)
S0298, Дж/моль×К	186,27	213,66	197,55	130,52

Решение. D_r S⁰₂₉₈=(ån_i S⁰_298i)_{продукты}–(ån_i iS⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (2×197,55 + 2×130,52) – (1×186,27 + 1×213,66) = 256,21 [Дж/K].

Пример 7.Определить направление самопроизвольного протекания реакции взаимодействия оксида кальция и воды с образованием дигидроксида кальция в стандартных условиях:

CaO_(кр) + H₂O_(ж) = Ca(OH)_2(кр).

Вещество	CaO(кр)	H2O(ж)	Ca(OH)2(кр)
DfG0298, кДж/моль	–603,46	–237,23	–897,52
DfH0298, кДж/моль	–635,09	–285,83	–985,12
S0298, Дж/моль×К	38,07	69,95	83,39

Решение. Направление самопроизвольного протекания реакции определяется по изменению энергии Гиббса (D_rG⁰ < 0).

1. Зная величины D_fG⁰ для реагентов, можно непосредственно вычислить изменение энергии Гиббса в ходе реакции:

D_r G⁰₂₉₈ = (å n_i D_fG⁰_i)_прод – (å n_i D_fG⁰_i)_{исх. вещества},

D_r G⁰₂₉₈ = (1(–897,52)) – [1(–603,46) + 1(–237,23)] = –56,83 (кДж).

Следовательно, данная реакция в стандартных условиях может самопроизвольно протекать в прямом направлении.

2. Изменение энергии Гиббса можно также вычислить по тепловому эффекту и энтропии реакции:

D_r G⁰₂₉₈ = D_r Н⁰₂₉₈ –298 D_r S ⁰₂₉₈,

D_r Н⁰₂₉₈ = (å n_i D_fН⁰_298i)_прод – (å n_i D_fН⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (ån_i S⁰_298i)_прод – (ån_i S⁰_298i) _{исх. вещества},

D_r Н⁰₂₉₈ = (1(–985,12)) – (1(–635,09) + 1(–285,83)) = –64,2 (кДж),

D_r S⁰₂₉₈ = (1×83,39) – (1×38,07 + 1×69,95) = –24,63 (Дж/K),

D_r G⁰₂₉₈ = –64,2 – 298(–24,63×10^-3) = –56,86 (кДж).

Результаты первого и второго расчетов, естественно, совпадают (с учетом погрешности).

Пример 8. Определить возможность самопроизвольного окисления ртути кислородом в стандартных условиях (прямая реакция) и температуру, при которой возможен самопроизвольный распад окиси ртути на ртуть и кислород (обратная реакция):

Hg(ж) + ½ O₂(газ) = HgO(кр).

Вещество	Hg(ж)	O2(газ)	HgO(кр)
DfH0298, кДж/моль			–90,88
S0298, Дж/моль×К	75,90	205,04	70,29

Решение. Изменение энергии Гиббса в ходе реакции вычисляют по тепловому эффекту и энтропии реакции при Т=298 К:

D_r G⁰(Т) » D_r Н⁰₂₉₈ – Т D_r S⁰₂₉₈,

D_r Н⁰₂₉₈ = (å n_i D_fН⁰_298i)_прод – (å n_i D_fН⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (ån_i S⁰_298i)_прод – (ån_i S⁰_298i) _{исх. вещества},

D_r Н⁰₂₉₈ = 1(–90,88) – (1×0 +½×0) = –90,88 кДж/моль,

D_r S⁰₂₉₈ = 1×70,29 – (1×75,90 +½×205,04) = –108,13 Дж/моль×K,

D_r G⁰₂₉₈ = –90,88 – 298(–108,13×10^-3) = –58,65 кДж/моль.

Поскольку D_rG⁰₂₉₈ < 0, то окисление ртути в стандартных условиях возможно.

Самопроизвольное разложение окиси ртути на кислород и ртуть возможно, если для обратной реакции 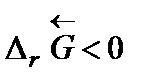. Поскольку 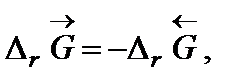то обратная реакция по отношению к окислению возможна, если D_rG⁰(Т) » D_r Н⁰ – Т D_r S ⁰ > 0, что выполняется при температуре выше 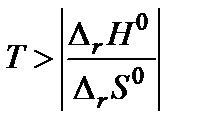= 840,47 К.

Библиографический список

1. Коровин, Н.В. Общая химия. М.: Высшая школа, 2000.

2. Стромберг, А.Г., Семченко Д.П. Физическая химия / Под ред. А.Г. Стромберга. М.: Высшая школа, 2001.

3. Фримантл, М. Химия в действии: В 2 ч. / Пер. с англ. М.: Мир, 1991.

4. Киселев, А.П., Крашенинников А.А. Основы общей химии: учебное
пособие / Балт. гос. техн. ун-т. СПб., 2012.

5. Кудряшов, И.В., Каретников Г.С. Сборник примеров и задач по физической химии: учебное пособие. М.: Высшая школа, 1991.

О Г Л А В Л Е Н И Е

1. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ.. 3

1.1. Энергия. 3

2. ПЕРВЫЙ ЗАКОН (НАЧАЛО) ТЕРМОДИНАМИКИ.. 6

2.1. Термодинамическая функция энтальпия. 7

2.2. Тепловой эффект реакции. 8

2.3. Закон Гесса. Термохимические расчеты.. 9

2.4. Зависимость теплового эффекта реакции от температуры.. 10

3. ВТОРОЙ ЗАКОН (НАЧАЛО) ТЕРМОДИНАМИКИ.. 11

3.1. Понятие энтропии. 12

3.2. Изменение энтропии в некоторых процессах. 14

3.3. Направленность самопроизвольных процессов. Свободная энергия Гиббса 16

4. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ.. 19

Библиографический список. 23

Барунин Анатолий Анатольевич, Маслобоев Дмитрий Степанович

Термодинамические расчеты

Редактор Г.М. Звягина

Корректор Л.А. Петрова

Подписано в печать 19.02.2016. Формат 60х84/16. Бумага документная.

Печать трафаретная. Усл. печ. л. 1,5. Тираж 200 экз. Заказ № 45.

Балтийский государственный технический университет

Типография БГТУ

190005, С.-Петербург, 1-я Красноармейская ул., д.1

А.А. БАРУНИН, Д.С. МАСЛОБОЕВ

ТЕРМОДИНАМИЧЕСКИЕ

РАСЧЕТЫ

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет «Военмех»

А.А. БАРУНИН, Д.С. МАСЛОБОЕВ

ТЕРМОДИНАМИЧЕСКИЕ РАСЧЕТЫ

Учебное пособие

Санкт-Петербург

УДК 541(075.8)

Б26

Барунин, А.А. Термодинамические расчеты: учебное пособие / А.А. Барунин, Д.С. Маслобоев; Балт. гос. техн. ун-т. – СПб., 2016. – 24 с. ISBN 978-5-85546-923-3   Излагаются в упрощенной форме краткие теоретические сведения по одной из основных тем курса химии – «Химическая термодинамика», а также методы и примеры решения типовых задач по расчету термодинамических характеристик химических реакций. Предназначено для студентов технических специальностей, изучающих дисциплину «Химия». Может быть использовано студентами при подготовке к зачету или экзамену.

Б26

УДК 541(075.8)

Р е ц е н з е н т канд. хим. наук, начальник отдела физико-хими-ческих методов исследования АО «ЦНИИМ» В.Н. Разуваев

Утверждено

редакционно-издательским

советом университета

ISBN 978-5-85546-923-3© Авторы, 2016

© БГТУ, 2016

ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ

Энергия

При рассмотрении закономерностей протекания химических процессов наиболее важными являются два типа закономерностей: энергетические и временные. Первые изучает химическая термодинамика, вторые – химическая кинетика.

Изначально термодинамика – это наука о «движении тепла». Она возникла в начале XIX века как теоретическая база создания тепловых машин (в основном паровых котлов), послуживших основой промышленной революции.

Термодинамическое описание химических процессов включает в себя решение двух задач:

1) изучение энергетических характеристик термодинамических систем;

2) возможность предсказать направление протекания самопроизвольных химических процессов и указать способы осуществления целенаправленных химических превращений.

Энергия – одно из основных физических понятий и потому не имеет исчерпывающего определения. Для наших целей примем, что энергия – это такая характеристика движения и взаимодействия тел, которая связана с их способностью совершать изменения в состоянии системы и внешней среды.

Видов энергии очень много: механическая, тепловая, электромагнитная, ядерная и т.д. Каждая из них может только видоизменяться, т.е. превращаться в другие виды энергии.

Термодинамическая система – это ограниченная область пространства, занятая ее элементами. Элементы системы (подсистемы) считаются однородными. Граница системы может быть и физической (стенки сосуда), и мысленной. Все, что вне системы, составляет окружающую среду.

Термодинамические системы бывают трех видов:

1) изолированные (нет обмена ни веществом, ни энергией с окружающей средой). Примеры – герметичный сосуд с газом с теплоизоляционной оболочкой, Вселенная в целом;

2) замкнутые (нет обмена веществом с окружающей средой). Пример – герметичный сосуд;

3) открытые (есть и энерго- и массообмен с окружающей средой). Примеры – костер, человек.

В химической термодинамике изучаются только изолированные и замкнутые системы.

Состояния систем характеризуются параметрами состояния(функциями процесса) и функциями состояния.

Параметры состояния системы – это свойства, однозначно характеризующие однородные части системы. Например, для идеального газа параметрами являются четыре свойства: давление р, объём V, температура T и количество молей ν. Любые три из них независимы. Это означает, что, задав произвольно любые три из четырех параметров, мы по уравнению состояния (в данном случае это будет уравнение состояния Клапейрона–Менделеева) найдем четвертый:

рV= ν RT.

Для более сложных систем могут появиться дополнительные параметры состояния, например химический состав.

Остановимся на параметре T. Это абсолютная температура в градусах Кельвина, которая всегда положительна. Она характеризует среднюю кинетическую энергию хаотического движения, приходящуюся на одну степень свободы частицы системы:

<E> =1/2 ikT,

где i – число степеней свободы, k – постоянная Больцмана, <E> – средняя кинетическая энергия хаотического движения; i=3 для одноатомных молекул (три направления свободного движения), i=5 для двухатомных (свободное движение плюс два вращения), i=6 для трехатомных и более (свободное движение плюс три вращения).

С точки зрения термодинамики температура – особый параметр. Она является индикатором направления передачи тепла: самопроизвольно тепло передается от более горячего тела к более холодному.

Существует понятие нулевого (или четвертого) закона термодинамики, который гласит: две системы, находящиеся в тепловом равновесии с третьей, находятся в равновесии и друг с другом. При этом все три системы характеризуются одинаковым значением определяющего это равенство параметра – температуры. Этот закон сформулировал Ральф Говард Фаулер в 1931 г.

Параметры термодинамической системы делятся на интенсивные и экстенсивные. Интенсивные параметры не зависят от количества вещества в системе (давление, температура, напряженность электрического поля и др.), а экстенсивные зависят (объем, масса, заряд и др.).

Параметры состояния связаны друг с другом функциональными зависимостями. Те из функций, которые не зависят от истории системы, т.е. от того, как она попала в данное состояние, называются функциями состояния. Они однозначно характеризуют это состояние.

В качестве примера приведём такую функцию состояния системы как внутренняя энергия U. К термодинамическому пониманию этой величины мы вернемся позже, пока же достаточно того, что мы знаем об энергии: в изолированных системах она сохраняется во времени.

Особую форму в термодинамике имеет время. Оно лишено такого качества, как длительность, и проявляется только как фиксация качественных изменений. В