Процесс массообмена между фазами

Общие сведения

Различают два основных вида процессов массопередачи:

1) массообмен между жидкостью и газом (паром) или ме­жду двумя несмешивающимися жидкостями;

2) массообмен между твердым телом и жидкостью, газом или паром (стр. 581).

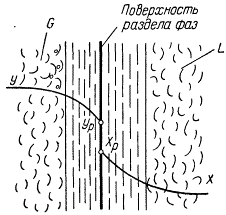
Процесс переноса вещества из одной фазы в другую в пер­вом случае можно представить следующим образом (рис. 1-3). Пусть концентрация распреде­ляемого вещества в фазе G вы­ше равновесной и вещество пе­реходит из фазы G в фазу L. Распределяемое вещество в фазе G переносится к поверх­ности раздела фаз, а в фазе L переносится от этой поверхно­сти. Перенос вещества в обеих фазах осуществляется путем молекулярной диффузии (т. е. диффузии молекул через слой носителя) и путем конвектив­ной диффузии (т. е. движущи­мися частицами носителя и распределяемого вещества).

В каждой фазе различают две области: ядро (основная масса) и пограничный слой, образующийся у поверхности раздела фаз. Перенос распределяемого вещества в ядре фазы, где обычно происходит интенсивное перемешивание, осуществ­ляется преимущественно путем конвективной диффузии. Вслед­ствие интенсивного перемешивания в ядре концентрация распре­деляемого вещества в каждом сечении системы почти постоянна.

Пограничный слой является областью резкого изменения кон­центрации распределяемого вещества. Перенос вещества в по­граничном слое осуществляется путем конвективной и молеку­лярной диффузии, причем по мере приближения к поверхности раздела фаз происходит затухание конвективных потоков и воз­растает роль молекулярной диффузии.

Концентрация распределяемого вещества в фазе G умень­шается от величины Y в ядре потока до величины Y_р на границе раздела фаз. В фазе L концентрация распределяемого вещества уменьшается от величины Х_р на границе раздела фаз до вели­чины X в ядре потока. При установившемся процессе на грани­це раздела фаз наблюдается равновесие, т. е. концентрации Y_р и Х_р являются равновесными.

Молекулярная диффузия

При молекулярной диффузии, согласно закону Фика, количе­ство диффундирующего через слой вещества пропорционально поверхности слоя F м², изменению концентрации по толщине слоя Δ_сл. кг/м³, времени τ сек и обратно пропорционально тол­щине слоя δ м. Таким образом

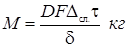(1-23)

где D — коэффициент пропорциональности, называемый коэф­фициентом диффузии.

Уравнение (1-23) называется уравнением диффузии. Оно аналогично уравнению теплопроводности: разности тем­ператур соответствует разность концентраций Δ_сл., коэффициенту теплопроводности — коэффициент диффузии D.

Из уравнения (1-23) определяем размерность коэффици­ента диффузии:

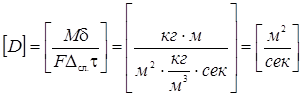
Коэффициент диффузии выражают также в м²/ч. Для пере­счета величины коэффициента диффузии из м²/ч в м²/сек надо разделить данный коэффициент на 3600:

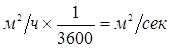
Коэффициент диффузии зависит от свойств диффундирую­щего компонента и среды, в которой происходит диффузия, а также от температуры и давления.

В справочных таблицах обычно приводятся коэффициенты диффузии D₀ в газах при температуре Т₀ = 273° К и абсолютном давлении Р₀ = 1 ат. При других абсолютных температурах Т и других абсолютных давлениях Р этот коэффициент определяется по формуле

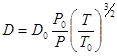(1-24)

из которой видно, что коэффициент диффузии в газах обратно пропорционален давлению и прямо пропорционален абсолютной температуре в степени .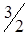

Для определения коэффициента диффузии газа А в газе В (или, что то же, газа В в газе А) при абсолютной температуре Т и абсолютном давлении Р ат можно пользоваться следующей зависимостью:

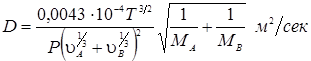(1-25)

где υ_A и υ_B — молекулярные объемы газов А и В;

M_A и М_B — молекулярные массы газов А и В.

Молекулярные объемы определяются как сумма атомных объемов υ элементов, входящих в состав соединений. Значения υ приведены ниже:

	υ
Водород………………………………………………………………………	3,7
Кислород
в метиловом эфире и сложных эфирах………………………………	9,1
в высших эфирах………………………………………………………
в кислотах………………………………………………………………
в прочих соединениях…………………………………………………	7,4
Азот
в первичных аминах…………………………………………………..	10,5
во вторичных аминах………………………………………………….
в прочих соединениях…………………………………………………	15,6
Углерод………………………………………………………………………..	14,8
Сера……………………………………………………………………………	25,6
Хлор…………………………………………………………………………...	24,6
Бром…………………………………………………………………………...
Воздух…………………………………………………………………………	29,9
Бензольное кольцо (вычитать)………………………………………………
Нафталиновое кольцо (вычитать)…………………………………………...
Водород (H2)……………………………………………………………….…	14,3

Коэффициенты диффузии в жидкостях значительно меньше, чем в газах. Для приближенного определения коэффициентов диффузии в жидкостях при 20° С можно пользоваться формулой

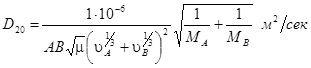(1-26)

где μ — вязкость растворителя, спз;

А и В — поправочные коэффициенты для диффундирующего вещества и растворителя.

Поправочные коэффициенты характеризуют отклонение свойств вещества от свойств неассоциированных веществ, для которых этот коэффициент равен единице. Для газов поправочный коэффициент А = 1. Для воды В = 4,7, для метилового и этилового спирта В = 2, для ацетона В = 1,15.

Коэффициент диффузии в жидкости при данной температуре t находят по соотношению

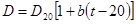(1-27)

причем температурный коэффициент b определяют по формуле

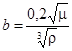
где μ — вязкость растворителя при 20° С, спз;

ρ — плотность растворителя, кг/м³.

Пример 1-7. Определить коэффициент диффузии паров бензола в воз­духе при 40° С (313° К) и абсолютном давлении 1 ат.

Решение. Молекулярный объем для бензола (C₆H₆)

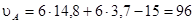
Молекулярный объем для воздуха υ_В = 29,9; молекулярные массы компонентов: М_A = 78 (для бензола), М_В = 29 (для воздуха). Подставляя все известные величины в формулу (1-25), получим:

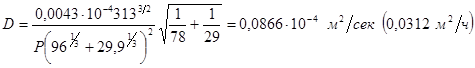
Пример 1-8. Определить коэффициент диффузии двуокиси углерода в воздухе при 25° С и абсолютном давлении Р = 20 ат

Решение. Коэффициент диффузии СО₂ в воздухе при Р₀ = 1 ат и T₀ = 273° К равен D₀ = 0,138·10^-4 м²/сек (0,0497 м²/ч). По формуле (16-24)

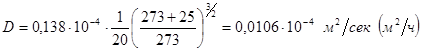
Пример 1-9. Определить коэффициент диффузии аммиака в воде при температуре 50° С.

Решение. Сначала определяем коэффициент диффузии при 20° С, подставляя в формулу (1-26) значения A = 1, В = 4,7, μ = 1 спз, υ_А = 15,6 + 3·3,7 = = 26,7 (для NH₃); υ_B = 2·3,7 + 7,4 = 14,8 (для воды), M_A = 17 (для NH₃), M_в = 18 (для воды):

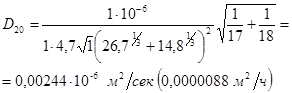
По формуле (1-27) при t = 50° С:

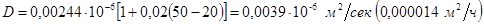
где 0,02 – температурный коэффициент b при μ = 1 спз и ρ = 1000 кг/м³.

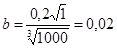
Конвективная диффузия

При конвективной диффузии количество вещества, переноси­мого в единицу времени из фазы, отдающей вещество, к поверх­ности раздела фаз (или от поверхности раздела фаз в фазу, вос­принимающую это вещество), пропорционально поверхности F и разности концентраций Δ_част.распределяемого вещества в фазе и у поверхности раздела:

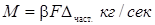(1-28)

Разность концентраций Δ_част. является частной движущей си­лой процесса, коэффициент пропорциональности β называется коэффициентом массоотдачи.

Подобно тому как уравнения (1-17) и (1-23) аналогич­ны уравнениям теплопередачи и теплопроводности, уравнение (1-28) аналогично уравнению конвективного теплообмена: коэффициент массоотдачи является аналогом коэффи­циента теплоотдачи и учитывает перенос вещества путем моле­кулярной и конвективной диффузии.

В зависимости от единиц, принятых для выражения Δ_част.,коэффициент массоотдачи β имеет такие же размерности, как и коэффициент массопередачи К.

Коэффициент массоотдачи зависит от гидродинамических, физических и геометрических факторов и определяется экспери­ментальным путем с обработкой данных при помощи теории подобия.

Приложение теории подобия к процессам массопередачи по­казало, что эти процессы определяются кинематическим крите­рием Re и диффузионными критериями Nu' и Pr', являющимися аналогами тепловых критериев Nu и Pr. Значения диффузионных критериев приведены в табл. 1.1.

Таблица 1.1

Критерий	Формула	Физический смысл критерия
Диффузионный критерий Нуссельта	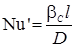(1-29)	Характеризует процесс массопередачи у поверхности раздела фаз
Диффузионный критерий Прандтля	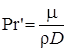(1-30)	Характеризует физические свойства среды

Критерии подобия являются безразмерными, поэтому при вычислениях входящие в формулу критерия величины должны быть взяты в одинаковой системе единиц. При пользовании системой СИ все величины, входящие в формулы (1-29) и (1-30), берутся в следующих единицах:

β_C — коэффициент массоотдачи, м/сек;

D — коэффициент диффузии, м²/сек;

μ — вязкость, н·сек/м²;

ρ — плотность, кг/м³;

l — определяющий геометрический размер, м.

При пользовании системой МКГСС величину μ берут в кгс·сек/м², ρ — в кгс·сек²/м⁴. При этом за единицу времени для β_C и D обычно прини­мают ч, тогда формула (1-30) принимает следующий вид:

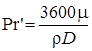
Критерии Re и Pr’ являются определяющими, критерий Nu’ — определяемым. Зависимость между критериями выра­жается в общем виде уравнением

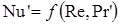(16-31)

По найденному значению Nu’ вычисляют коэффициент массоотдачи при помощи формулы (1-29), из которой следует:

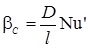(16-32)

Пересчет β_C в другие размерности коэффициента β произ­водится аналогично пересчету коэффициента массопередачи по формулам (1-19) — (1-22).

Конкретные зависимости критерия Nu’ от Re и Pr’ будут приведены при рассмотрении отдельных процессов.

Подобие процессов массопередачи

Условия подобия процессов массопередачи можно вывести аналогично условиям теплового подобия. Обозначив через 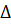' изменение кон­центрации по толщине пограничного слоя и через 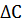изменение концентрации по длине (высоте) аппарата, можно написать условие подобия для двух аппаратов (1 и 2) в следующем виде:

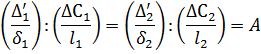
Здесь представляет собой градиент концентрации по толщине пограничного слоя, 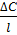– градиент концентрации по длине (высоте) аппарата.

Объем фазы, проходящий через аппарат, в единицу времени, равен 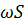( 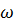- скорость фазы, S- площадь сечения аппарата).Если концентрация фазы изменилась по длине (высоте) аппарата на 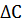, то количество вещества, перешедшего в эту фазу, будет 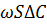.Такое же количество вещества будет передается путем диффузии через пограничный слой и, согласно уравнению диффузии, составляет: 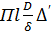, где П- периметр пограничного слоя.Таким образом

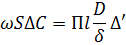
Заменяя эквивалентным диаметром d_экв., получим:

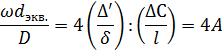
Таким образом, условием подобия процессов массопередачи является ра­венство отношения А или, что то же, равенство диффузионного критерия Пекле:

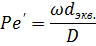
Диффузионный критерий Пекле Ре' характеризует отношение поперечного градиента концентрации (по толщине пограничного слоя) к продольному гра­диенту (по длине или высоте аппарата).

При практических расчетах критерий Пекле заменяют диффузионным критерием Прандтля:

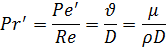
где 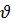— кинематическая вязкость фазы.

Условием подобия процессов массопередачи в двух аппаратах является равенство критериев Ре, а также критериев Рr'.

Количество вещества, передаваемого через пограничный слой, было опре­делено как 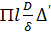. Это же количество вещества, согласно уравнению мас-

соотдачи (1-28), равно 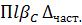, где 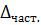- движущая сила массоотдачи (разность концентраций у поверхности раздела фаз и в ядре фазы). Отсюда

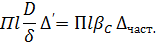
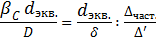
Правая часть этого уравнения для подобных систем одинакова. Следова­тельно, для них одинакова и левая часть, т. е. одинаков диффузионный кри­терий Нуссельта:

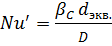
Связь коэффициента массопередачи и
коэффициентов массоотдачи

Рассмотрим переход вещества из фазы G в фазу L (см. рис. 1-3). Уравнение конвективного массообмена для фазы G:

Для фазы L: 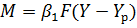(1-33)

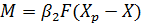(1-34)

где 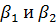—коэффициенты массоотдачи для фаз G и L;

F— поверхность соприкосновения фаз.

Пусть линия равновесия представляет собой прямую с тан­генсом угла наклона, равным k, т. е.

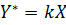
тогда на границе раздела фаз

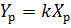
Таким образом, концентрации в фазе L можно выразить че­рез концентрации в фазе G:

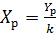и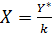

где Y* — концентрация в фазе G, равновесная с концентра­цией X в ядре

фазы L.

Подставляя значения Х_р и X в уравнение (1-34), получим:

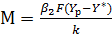(1-35)

Определим из уравнений (1-33) и (1-35) движущую силу процесса:

;

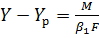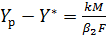
Складывая почленно эти уравнения, получим:

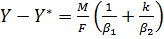(1-36)

Уравнение массопередачи для рассматриваемого случая имеет следующий вид:

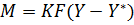
или 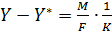(1-37)

Приравнивая правые части уравнений (1-36) и (1-37), на­ходим зависимость между коэффициентом массопередачи К и коэффициентами массоотдачи :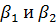

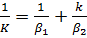(1-38)

Уравнение (1-38) аналогично уравнению, устана­вливающему связь между коэффициентом теплопередачи k и коэффициентами теплоотдач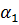и и .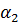

В уравнении (1-38) член 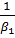выражает сопротивление переходу вещества в фазе G, член 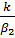- сопротивление в фазе L.

Если коэффициент 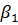велик, то член 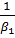мал и, как видно из уравнения (1-38), 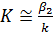. В этом случае сопротивлением в фазе G можно пренебречь.

При большом коэффициенте 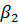член 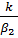мал и, как видно из

уравнения (1-38), 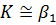.В этом случае сопротивлением в фазе L можно

пренебречь.

Уравнение (1-38) выведено при условии линейной зависи­мости между равновесными концентрациями Y* и X. В случае отсутствия такой зависимости линия равновесия не будет прямой и в качестве k надо брать тангенс угла наклона касательной к линии равновесия в данной точке. При этом величины k и К будут изменяться по длине аппарата. При расчетах берут сред­нее значение k или же разделяют аппарат по длине на несколько участков, считая к постоянным в пределах каждого участка.

Массообмен с участием твердой фазы

В твердой фазе конвекция отсутствует и перенос вещества характеризуется уравнением массопроводности, аналогичным уравнению молекулярной диффузии:

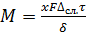(1-39)

где х — коэффициент пропорциональности, имеющий размер­ность коэффициента диффузии и называемый коэффи­циентом массопроводности.

Если распределяемое вещество переносится из твердой фазы в омывающую ее жидкую, газовую или паровую фазу, то в пре­делах твердой фазы вещество перемещается вследствие массопроводности к границе раздела фаз и далее переносится в омывающую фазу путем конвективной диффузии.

Перемещение вещества вследствие массопроводности яв ляется неустановившимся процессом. В начальный момент кон­центрация вещества (Y₁) одинакова во всем объеме твердого тела. В момент времени т средняя концентрация (Y) ниже на­чальной, причем распределение концентрации в твердом теле неравномерно — в центре концентрация больше, у границы раз­дела фаз — меньше. При 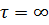концентрация выравнивается и стремится к равновесной (Y*).