Светогеометрия «вакуума» и основы Алгебры сигнатур

Светогеометрия «вакуума» и основы Алгебры сигнатур

Михаил Батанов[1], к.т.н., доцент,

кафедра 207 Московского авиационного института

Москва, Россия

Аннотация:В рамках программы геометризации физики, к которой относятся работы автора [1, 2, 3], рассмотрены физические и математические основы светогеометрии вакуума и Алгебры сигнатур. Вакуум исследуется посредством зондирования его взаимно перпендикулярными монохроматическими лучами света с различными длинами волн. В результате получается иерархия вложенных друг в друга световых 3D-ландшафтов (l_m¸n-вакуумов). Рассмотрены неискривленное и искривленное состояния локального участка l_m¸n-вакуума на основании математического аппарата Алгебры сигнатур. Сформулировано «вакуумное условие», на основании определения «вакуумного баланса». Рассмотрены инертные свойства l_m¸n-вакуума. Приведено кинематическое обоснование возможности разрыва локального участка l_m¸n-вакуума. На основании изложенных здесь основ Алгебры сигнатур в статьях [2, 3] получены метрико - динамические модели всех элементарных частиц, входящих в состав Стандартной модели. В данной работе вводятся новые понятия, поэтому в конце статьи приведен «Указатель определений новых терминов».

Ключевые слова:Вакуум, светогеометрия, пустота, спинтензор, сигнатура, стигнатура метрика, аффинное пространство, метрическое пространство, геометризированная физика.

Постньютоновский вакуум

Когда ты сражаешься с монстрами, остерегайся, чтобы самому не стать монстром. И если ты долго всматриваешся в Бездну, то Бездна всматривается в тебя.

Ф. Ницше

“Jenseits Gut und Böse”

Вакуум (от лат. vacuus – пустой) это самый сложный объект, с которым когда-либо сталкивался человеческий рассудок. «Пустота» – это Все и Ничего в потенции. Она одновременно: совершенная Наполненность и полная Отсутственность; абсолютный Покой и абсолютное Движение. Интуитивно мы ощущаем, что у «вакуума» не должно быть краев, и нет дна. Но от нас полностью ускользает понимание: – Она иллюзия или реальность?

В конце 19-го и в начале 20-го веков в качестве примитивной модели «вакуума» рассматривался объем пространства (рис. 1.1), в котором отсутствуют какие-либо материальные частицы. В наши дни в ряде областей техники часто сильно разряженный газ называют техническим вакуумом, полагая, что абсолютно чистый вакуум – это синоним пустоты.

Рис. 1.1. Локальный участок пустой 3-мерной протяженности, т.е. классического вакуума 19-го века

Позднее в квантовой теории поля возникли представления о физическом вакууме, как о наложении «нулевых» осцилляций множества квантованных (скалярных, векторных, спинорных, тензорных, комплексных и т.д.) полей. Были развиты представления о поляризации, конденсатах, дислокациях и других проявлениях физического вакуума. В последнее время добавилась необходимость «наполнить» вакуум некой темной энергией и темной материей для объяснения ряда космологических эффектов. Таким образом, в современных научных представлениях даже совершенно свободный от молекул и атомов объем пространства (физический вакуум) – это многослойный, повсеместно чрезвычайно сложно флуктуирующий объект, практически с бесконечной плотностью энергии. Вместе с тем, в среднем физический вакуум проявляет себя как «пустота», поэтому возникает необходимость «избавиться» от бесконечной плотности его энергии (ультрафиолетовой расходимости) посредством перенормировок (т.е. за счет введения дополнительных контр-членов в лагранжианы бозонных и фермионных полей).

Рис. 1.2. Фрактальная иллюстрация чрезвычайно сложно насыщенного вакуума

и вакуумных образований в нем

С другой стороны, множество попыток нескольких поколений ученых "нащупать" субстанциональную основу окружающего Бытия в виде: эфира, флогистона, эссенции, амеров, флюидов, электричества, квинтэссенции и т.д. не увенчались успехом.

Рис. 1.3. Измерительная решетка состоящая из часов и линеек

Провал программы обнаружения тонкой материальной основы Бытия привел к развитию представлений о 4-мерном пространственно-временном континууме. Новый подход базировался на синтезе эмпиризма и рационализма, суть которого применительно к рассматриваемому вопросу сводилась к следующему утверждению: – «Да, мы не знаем, из чего состоит окружающая протяженность (т.е. «пустота»). Но с помощью всюду расставленных часов и линеек (рис. 1.1) мы можем «вырисовать» пространственно-временную 4-мерную координатную сетку, которая повторяет контуры протяженной реальности». Многие ученые начала 20-го века хорошо понимали, что это только умозрительные «контуры реальности», а не сама реальность. Но со временем укоренилось мнение, что 4-мерный пространственно-временной континуум – это и есть то, что нас окружает, а массивные материальные тела искривляют его.

На самом деле пространство-время – это всего лишь ментальная модель протяженной реальности, т.е. интеллектуальная «конструкция», отображающая ряд геометрических и динамических свойств «вакуума». Данная логическая «конструкция» имеет границы применимости, поэтому в наше время она стала причиной ряда научных проблем.

Одной из основных современных проблем является несоответствие физического вакуума (т.е. совокупности нулевых осцилляций квантованных полей) с 4-мерным пространственно-временным континуумом. При попытке проквантовать искривленное пространство-время, оно «взрывается», т.к. квантовая физика не допускает бесконечно точную локализацию места без полной неопределенности в его состоянии движения. Физический вакуум – это своего рода бурлящий «бульон» из множества рождающихся и исчезающих частиц и античастиц различных сортов, а пространство-время – это гладкое многообразие с мощностью континуума.

Вместе с тем физический вакуум и пространственно-временной континуум объединяет Лоренц инвариантность обеих логических конструкций.

Другой проблемой является не только вопросы, связанные с философским осмыслением категорий: «пространство» и «время», соединенных в единый «пространственно-временной континуум», но и сам процесс измерения расстояния и длительности сопряжен с множеством систематических и случайных погрешностей, величина которых часто оказывается соизмеряемой с пространственно-временными искривлениями.

В этой статье предпринята попытка построения светогеометрической модели вакуума (т.е. «пустой» протяженности), которая, на наш взгляд, более адекватно отражает свойства протяженной реальности, чем пространственно-временной континуум, при отсутствии противоречий с квантовой физикой.

Для изложения основ Алгебры сигнатур (Алсигны) мы в начале возвращаемся к максимально упрощенному рассмотрению «Пустоты» в виде чистого технического вакуума 19 века, который будем называть постньютоновским вакуумом, или для сокращения «вакуумом».

Отметим, что в этой статье рассматривается только объективный «вакуум», который находится снаружи по отношению к наблюдателю, поскольку «субъективная пустота», находящаяся внутри наблюдателя (т.е. пространственная подоснова для человеческих впечатлений, иллюзий и галлюцинаций), обладает иными свойствами, и требует дополнительного исследования.

Определение № 1.1 Постньютоновский вакуум («вакуум») – это реальное 3-мерное пространство без материи, находящееся вне сознания наблюдателя.

Впоследствии, по мере развития светогеометрии и Алгебры сигнатур, модель «Вакуума» будет все более и более усложняться, вплоть до исследования Его Паро-аномальных и Био - Психических проявлений [4 – 9].

Светогеометрия объективного «вакуума» (т.е. постньютоновского вакуума) строится на основании алгоритмов раскрытия Четырехбуквенного Имени ВСЕВЫШНЕГО (ТЕТРАГРАММАТОНА) [4]. Это вселяет надежду на сближение объективных воззрений на окружавшую реальность с субъективной Психо-Физикой Разумного Бытия.

2. Продольное расслоение плоского «вакуума» на l_m¸n-вакуумы

Вначале рассмотрим 3-мерную область постньютоновского вакуума («вакуума»), в которой отсутствуют какие-либо искривления и течения.

Мы не знаем, из чего состоит «вакуум», но нам достоверно известно, что через него распространяются лучи света (электромагнитные волны или фотоны) со скоростью света

с = 2,99792458 ×10⁸м/с. (2.1)

На данном этапе мы не задаемся вопросом, что такое луч света и как он проходит через исследуемый 3-мерный участок «вакуума». Просто констатируем экспериментальный факт, что фотон, испущенный из точки А «вакуума», за промежуток времени Δt достигает его точки Б.

Если метрико-динамическое состояние исследуемого объема «вакуума» неизменно, то линия, по которой прошел фотон (или последовательность фотонов – луч света), остается неизменной. Именно совокупность таких взаимно перпендикулярных стационарных линий (лучей света) (рис. 2.1, 2.2) и является предметом рассмотрения настоящей работы.

Рис. 2.1. Стационарные лазерные лучи света, визуализированные с помощью аэрозоли https://heatmusic.ru/product/ls-systems-beam-green/ 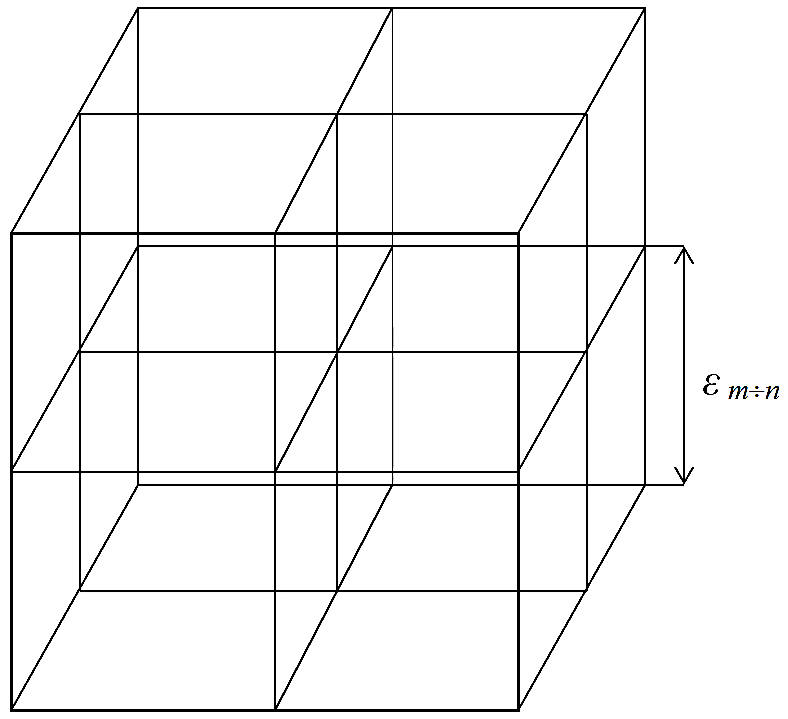      Рис. 2.2. Трехмерная решетка в «вакууме», состоящая из взаимно перпендикулярных стационарных монохроматических лучей света с длиной волны lm¸n и длиной ребром кубической ячейки ε m¸n ~ 102 lm¸n

Определение № 2.1 Определение № 2.1Луч света в момент времени t – это линия, по которой прошел фотон в «вакууме» за интервал времени от момента его испускания t₀ до t. [определение Дэвида Рида (David Reid)].

Разделим весь диапазон длин световых (электромагнитных) волн l на поддиапазоны от 10^m см до 10^{m +1} см, где m натуральные числа.

Если через исследуемый объем «вакуума» посылать монохроматические лучи света с определенной длиной волны l_m¸n (из диапазона Δl =10^m ¸ 10ⁿ см, где n = m +1) с трех взаимно перпендикулярных направлений, то в этом объеме можно «визуализировать» стационарную 3-мерную световую сетку (своего рода световую «кристаллическую» решетку) (рис. 2.1, 2.2) с длиной ребра кубической ячейки

ε _m¸n ~ l_m¸n, (2.2)

Данную 3-мерную сетку будем условно называть световым 3D-ландшафтом или l_m¸n -вакуумом.

Определение № 2.2l_m¸n-вакуум – это 3D-ландшафт в «вакууме», который состоит из пересечения стационарных монохроматических лучей света с длиной волны l_m¸n из диапазона Δl =10^m ¸ 10ⁿ см, где n = m +1 (рис. 2.1 и 2.2). Толщина лучей света по сравнению с исследуемым объемом «вакуума» стремиться к нулю, т.е. выполняется условие применимости геометрической оптики.

Последовательно прозондировав исследуемый объем «вакуума» монохроматическими лучами света с длиной волны l_m¸n из всех поддиапазоновΔl = 10 ^m ¸ 10ⁿ см, получим практически бесконечное количество вложенных друг в друга l_m¸n-вакуумов (рис. 2.3).

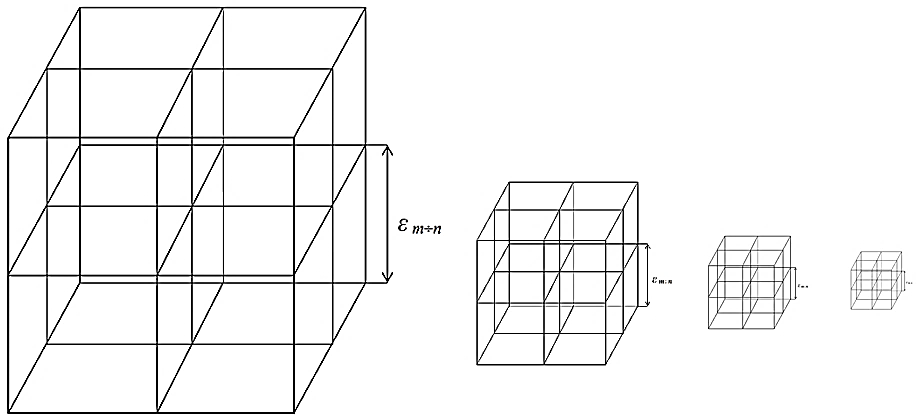
Рис. 2.3. Дискретный наборсветовых3D-ландшафтов (l_m¸n -вакуумов) одного и того же 3-мерного

участка «вакуума», где l _m¸n > l _{m+1¸ n+1} > l _{m+2¸ n+2} > l _{m+3¸ n+3} > l _{m+4 ¸ n+4 …}

Если l _m¸n > l _{m+1¸ n+1}, то размеры кубических ячеек 3D-ландшафтов (l_m¸n-вакуумов) ε _m¸n > ε _m+1¸n+1. Так осуществляется продольное «расслоение» исследуемого объема «вакуума» на бесконечный дискретный ряд световых 3D-ландшафтов (l_m¸n -вакуумов).

Определение № 2.3Продольное расслоение «вакуума» – это представление пустой 3-мерной протяженности в виде бесконечной дискретной последовательности вложенных друг в друга l_m¸n-вакуумов.

Продольное расслоение «вакуума» на бесконечное количество l_m¸n-вакуумов аналогично представлению о физическом вакууме как о квантовой жидкости, состоящей из фотонных частиц, расположенных в определенном порядке наподобие кристаллической решетки. Так же полный набор l_m¸n-вакуумов соответствует представлению квантовой теории поля о самом низком (нулевом) энергетическом уровне физического вакуума, который состоит из бесконечного множества гармонических осцилляторов, непрерывно и повсеместно колеблющихся с собственными частотами ω_m¸n = с/l_m¸n и нулевыми энергиями Е_о = ħ ω_m¸n /2, где ħ = 1,054572·10⁻³⁴ Дж×с – приведенная постоянная Планка.

Субконт и антисубконт

Важным аспектом развиваемой здесь теории является утверждение, что объектом исследования является 3-мерный объем «вакуума» (рис. 2.2). Из этого постулата следует основная формула аффинной светогеометрии (4.2)

cdt = dl = (dx²+ dy² + dz²) ^½ = |idx + jdy +kdz| (7.1)

(гдеi, j, k–ортогональные единичные вектора), и основная формула метрической светогеометрии (4.3)

c²dt² = dx²+ dy² + dz². (7.2)

Преобразование тождества (7.2) приводит к системе из двух квадратичных форм:

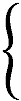ds^(–)2 = c²dt² – dx² – dy² – dz² = dx₀² – dx₁² – dx₂² – dx₃² = 0 с сигнатурой (+ – – –) (7.3)

ds⁽⁺⁾² = – c²dt² + dx² + dy² + dz² = – dx₀² + dx₁² + dx₂² + dx₃² = 0 с сигнатурой (– + + +) (7.4)

Из данной системы уравнений следует два «технических» вывода:

1. Квадратичные формы (7.3) и (7.4) можно условно интерпретировать как метрики двух 4-мерных «сторон» одного и того же 4 + 4 = 8 = 2³ - мерного метрического пространства, которое будем называть «2³-l_m¸n - вакуумной протяженностью».

Определение № 7.1 2^k-l_m¸n-вакуумная протяженность – это, вспомогательная логическая «конструкция», означающая пространство (с мощностью континуума) с 2^k математическими измерениями (где k = 3, 4, 5, … , ¥), которое «высвечивается» из «вакуума» посредством зондирования ее монохроматическими лучами света с длиной волны l_m¸n.

Самая простая 2³-l_m¸n -вакуумная протяженность имеет две «стороны»:

– 4-мерное пространство Минковского с метрикой (7.3) и сигнатурой (+ – – –);

– 4-мерное антипространство Минковского с метрикой (7.4) и сигнатурой (– + + +).

Рис. 7.1. Изогнутая двухстороння поверхность листа бумаги

Алгоритмы перехода от протяженных логических конструкций с 2^k математическими измерениями к 3 - мерному объему «вакуума» будут рассмотрены ниже.

Несмотря на то, 2³-l_m¸n -вакуумная протяженность являются чисто логической 4+4 = 8 - мерной конструкцией, из нее могут быть получены физические следствия. Поясним это на следующем 2 + 2 = 4 - мерном примере.

У листа бумаги (толщиной которого можно пренебречь) имеется две 2-мерных страницы (рис. 7.1). Поэтому лист бумаги можно рассматривать в качестве аналога 2 + 2 = 4-мерной протяженности.

Если лист бумаги не деформирован, то обе его «стороны» с точки зрения геометрии практически одинаковы. Однако если лист перегнуть, то с одной его 2-мерной стороны все ее элементарные площадки немного расширятся, а с другой сопряженной 2-мерной стороны – все элементарные площадки немного сожмутся.

Точно так же при искривлении локального участка «вакуума», в нем по необходимости (которая определяется «вакуумным условием») одновременно возникают, как локальные сжатия, так и локальные расширения, что автоматически учитывается как минимум «двусторонним» рассмотрением ее 4 + 4 = 8-мерной метрической протяженности. Таким образом, формальные математические приемы приводят к вполне осмысленным физическим следствиям.

Если учитывать толщину листа бумаги, то в качестве элемента рассмотрения должен быть уже элементарный кубик, находящийся между двумя сторонами листа. При этом, как будет показано ниже, потребуется рассмотрение континуальной протяженности с 4×16 = 8×8 = 64 математическими измерениями.

При еще более тонком рассмотрении понадобится уже 16 × 16 = 256-мерная протяженность, и т.д. до 2^k-мерного математического пространства (где k → ∞).

Таким образом, в светогеометрии «вакуума», развиваемой в рамках Алгебры сигнатур, имеется только 3 физических пространственных измерения «вакуума» и одно временное измерение, связанное со сторонним наблюдателем, а также 2^k математических (т.е. формальных или технических) измерений, где k = 3, 2, …, ∞ зависит от уровня рассмотрения исследуемого объема «вакуума».

Еще раз укажем на особенность времени в развиваемой здесь теории. В светогеометрии время не является атрибутом исследуемого участка «вакуума». Напомним, что в радиолокационном способе исследования метрико-динамических свойств локального участка «вакуума» (п. 3), интервал времени dt измеряется в приемо-передатчике радиолокационной установки (РЛУ) (рис. 3.1), который находится за пределами этого участка. Это соответствует часам стороннего наблюдателя, которые никакого отношения к изучаемому участку «вакуума» не имеют.

Когда задачу удается свести к двухстороннему рассмотрению, т.е. к исследованию 2³-l_m¸n-вакуумной протяженности, то предлагается ввести сокращенные условные обозначения:

Определение № 7.2 «Внешняя» сторона 2³-l_m¸n -вакуумной протяженности (или субконт) – это 4-мерная протяженность, локальные метрико-динамические свойства которой задаются метрикой

ds^{(+ – – –)2} = g_ij^(–)dxⁱdx^j с сигнатурой (+ – – –) (7.5)

где 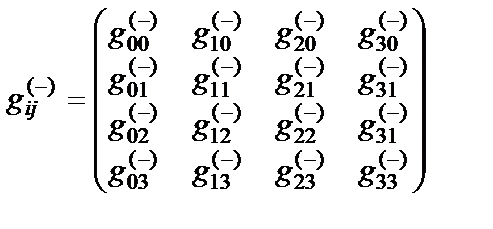(7.6)

- метрический тензор «внешней» стороны 2³-l_m¸n -вакуумной протяженности (или субконта).

В случае

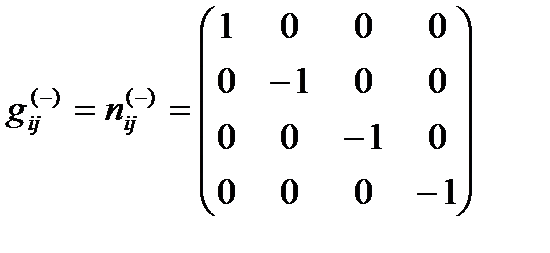(7.7)

«субконт» является синонимом 4-мерного пространства Минковского с метрикой (7.3) и сигнатурой (+ – – –);

Определение № 7.3 «Внутренняя» сторона 2³-l_m¸n -вакуумной протяженности (или антисубконт) – это 4-мерная протяженность, локальные метрико-динамические свойства которой задаются метрикой

ds^{(– + + +)2} = g_ij⁽⁺⁾dxⁱdx^j, с сигнатурой (– + + +) (7.8)

где 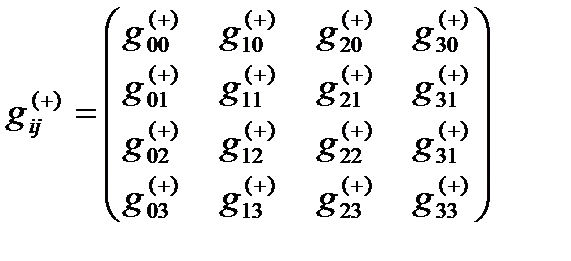(7.9)

- метрический тензор «внешней» стороны 2³-l_m¸n-вакуумной протяженности (или антисубконта).

В случае

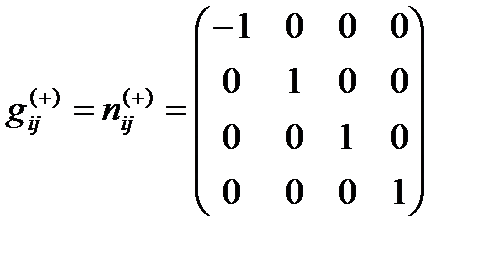(7.10)

«антисубконт» является синонимом 4-мерного антипространства Минковского с метрикой (7.4) и сигнатурой (– + + +).

В определениях 7.2 и 7.3 для сокращения изложения ведены два вспомогательных понятия:

Определение № 7.4 «Субконт» (сокращ. от «субстанциональный континуум») – это умозрительная сплошная упруго-пластическая 4-мерная псевдосреда, локальные метрико - динамические свойства которой задаются метрикой (7.6).

Определение № 7.5 «Антисубконт» (сокращ. от «антисубстанциональный континуум») – это умозрительная сплошная упруго-пластическая 4-мерная псевдосреда, локальные метрико-динамические свойства которой задаются метрикой (7.8).

Понятия «субконт» и «антисубконт» не имеют отношения к реальности. Это вспомогательные 4-мерные псевдосреды, которые являются синонимами соответственно «внешней» и «внутренней» сторон 2³-l_m¸n -вакуумной протяженности, и вводятся они только для удобства восприятия ряда 3-мерных упруго-пластических процессов, протекающих в «вакууме».

Реальным объектом в Алгебре сигнатур является только 3-мерный объем «вакуума». Все многомерные математические выкладки сводятся к вычислению только 3-мерных физических величин, характеризующих метрико-динамическое состояние локального или глобального участка «вакуума».

Алгебра стигнатур

Выше были рассмотрены физические основы светогеометрии «вакуума». Далее будут в основном затрагиваться формальные геометрические и математические аспекты данной теории.

Как бы далее ни усложнялся формальный математический аппарат Алгебры сигнатур, следует помнить, что геодезическими линиями исследуемого 3D-ландшафта (или l_m¸n-вакуума) являются монохроматические бесконечно тонкие лучи света с длиной волны l_m¸n. При этом основным «предметом» рассмотрения является бесконечно малая 3-мерная кубическая ячейка l_m¸n-вакуума в окрестности точки О (рис. 6.1, 6.2), с каждым углом которой связано по два вращающихся 4-базиса, показанных на рис. 6.3.

Каждый из этих шестнадцати 4-базисов задает направление осей 4-мерного аффинного пространства со своей особой характеристикой, которую будем называть «стигнатура».

Рис. 8.1. База со стигнатурой {+ + + +}

Чтобы ввести характеристику «стигнатура» аффинного пространства, сначала определим понятие «база». Выберем из 16-и 4-базисов, показанных на рис. 6.3, в качестве «базы» пятый 4-базис e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) (рис. 8.1) и условно примем, что направления всех его единичных базисных векторов положительны

e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) = (+1, +1,+ 1, +1) ® {+ + + +}. (8.1)

Здесь введено сокращенное обозначение {+ + + +}, которое в дальнейшем будем называть «стигнатурой» аффинного (векторного) пространства, задаваемого 4-базисом e⁽⁵⁾.

Определение № 8.1 «База» – это один из 16-и 4-базисов, показанных на рис. 6.3, направления всех 4-х единичных векторов которого условно приняты положительными, поэтому стигнатура базы всегда {+ + + +}.

Определение № 8.2 «Стигнатура» 4-базиса – это совокупность знаков, соответствующих направлениям базисных векторов по отношению к направлениям базисных векторов «базы».

Относительно произвольно выбранной «базы» (т. е. 4-базисаe⁽⁵⁾) оси всех остальных 4-базисов, показанных на рис. 6.3, имеют следующие знаки:

Таблица 8.1

ei(1) (e0(1), e1(1), e2(1), e3(1)) = = (1, 1, –1, 1) ® {+ + – +}   ei(2) (e0(2), e1(2), e2(2), e3(2)) = = (1, –1, –1, –1) ® {+ – – –}   ei(3) (e0(3), e1(3), e2(3), e3(3)) = = (1, 1, –1, –1) ® {+ + – –}   ei(4) (e0(4), e1(4), e2(4), e3(4)) = = (1, –1, –1, 1) ® {+ – – +}   ei(5) (e0(5), e1(5), e2(5), e3(5)) = = (1, 1, 1, 1) ® {+ + + +}   ei(6) (e0(6), e1(6), e2(6), e3(6)) = = (1, –1, 1, –1) ® {+ – + –}   ei(7) (e0(7), e1(7), e2(7), e3(7)) = = (1, 1, 1, –1) ® {+ + + –}   ei(8) (e0(8), e1(8), e2(8), e3(8)) = = (1, –1, 1, 1) ® {+ – + +}

ei(9) (e0(9), e1(9), e2(9), e3(9)) = = (–1, 1, –1, 1) ® {– + – +}   ei(10) (e0(10), e1(10), e2(10), e3(10)) = = (–1, 1, –1, –1) ® {– – – –}   ei(11) (e0(11), e1(11), e2(11), e3(11)) = = (–1, 1, –1, –1) ® {– + – –}   ei(12) (e0(12), e1(12), e2(12), e3(12)) = = (–1, –1, –1, 1) ® {– – – +}   ei(13) (e0(13), e1(13), e2(13), e3(13)) = = (–1, 1, 1, 1) ® {– + + +}   ei(14) (e0(14), e1(14), e2(14), e3(14)) = = (–1, –1, 1, –1) ® {– – + –}   ei(15) (e0(15), e1(15), e2(15), e3(15)) = = (–1, 1, 1 –1) ® {– + + –}   ei(16) (e0(16), e1(16), e2(16), e3(16)) = = (–1, –1, 1, 1) ® {– – + +}

Все стигнатуры, приведенные в табл. 8.1, объединяются в 16-компонентную матрицу:

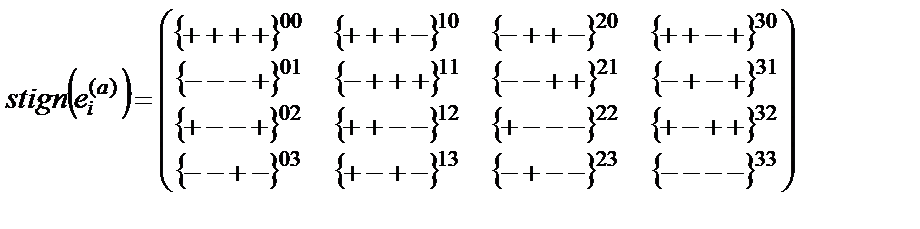. (8.2)

Эта матрица представляет собой отдельный математический объект, обладающий уникальными свойствами. Перечислим некоторые из них:

1. Сумма всех 16-и стигнатур (8.2) равна нулевой стигнатуре

{+ + – +} + {+ – – –} + {+ + – –} + {+ – – +} +

+ {+ + + +} + {+ – + –} + {+ + + –} + {+ – + +} + (8.3)

+ {– + – +} + {– – – – } + {– + – –} + {– – – +} +

+ {– + + +} + {– – + –} + {– + + –} + {– – + +} = {0000}.

2. Сумма всех 64 знаков, входящих в матрицу (8.2) равна нулю (32 «+» + 32 «–» = 0).

3. Возможны четыре бинарные комбинации знаков:

, (8.4)

или в транспонированном виде

. (8.5)

Всевозможные сочетания данных бинарных комбинаций знаков образуют 16 вариантов стигнатур:

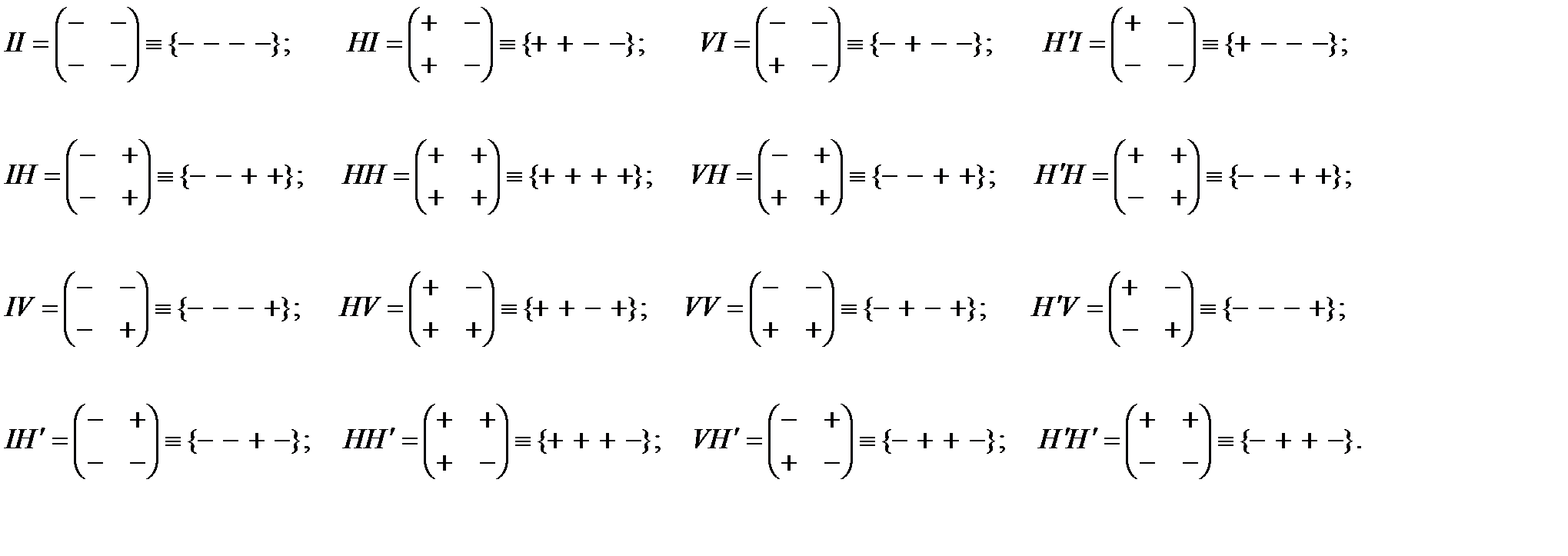(8.6)

Светогеометрия «вакуума» строится на основании Алгоритмов Раскрытия Великого и Грозного Имени ВСЕВЫШНЕГО ה-ו-ה-י (Йюд-Г’ей-Вав-Г’ей) [4].

Одна из форм раскрытия Имени ה-ו-ה-י (H¢ V H I i) является «Древо десяти Сфирот», которое можно получить путем возведения в кронекеров квадрат двурядной матрицы:

(8.6b)

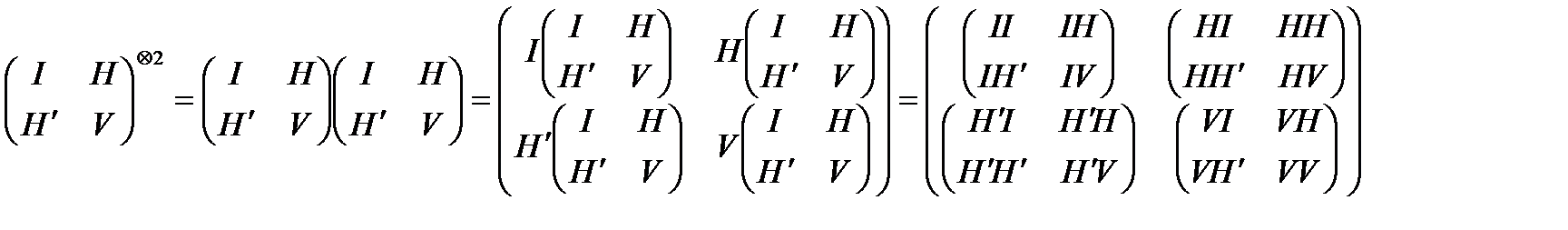
Компоненты данной матрицы соответствуют 10 Сфирот

i (коц) II Кетер

IHH Хохма

H VV Бина (8.6c)

V IV, IH, IH¢, VH, VH¢, HH¢ Тиферет*

VI, HI, H¢I, HV, H¢V, H¢H

H¢H¢H¢ Малхут

где Тиферет* состоит из шести Сфирот:

Хесед (IV = VI) Гвуга (IH = HI) Тиферет (IH¢ = H¢I) (8.6d)

Нецах (VH=HV) Ход (VH¢ = VH¢) Йесод (HH¢ = H¢H)

4. Кронекеров квадрат двурядной матрицы бинарных стигнатур образует матрицу 16 стигнатур (8.2):

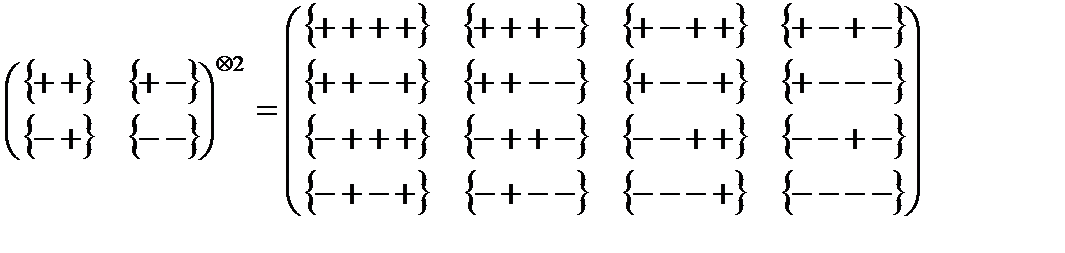(8.7)

где Ä – символ, означающий кронекерово умножение.

5. Если матрицам (8.6) вернуть исходные единицы, то получим двурядные матицы

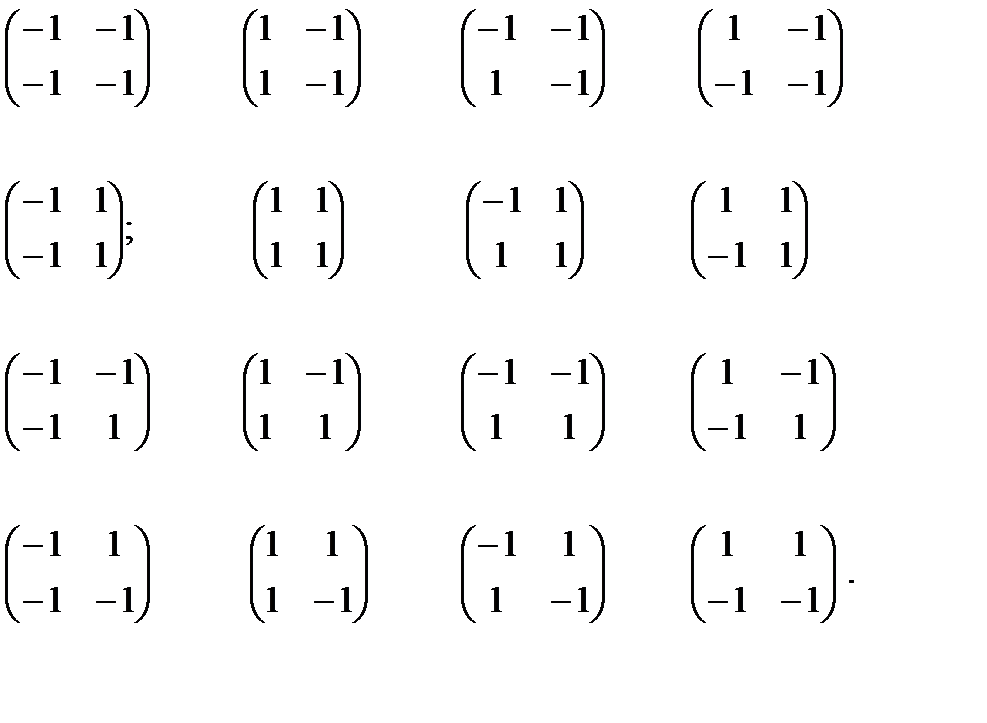(8.8)

Из них восемь:

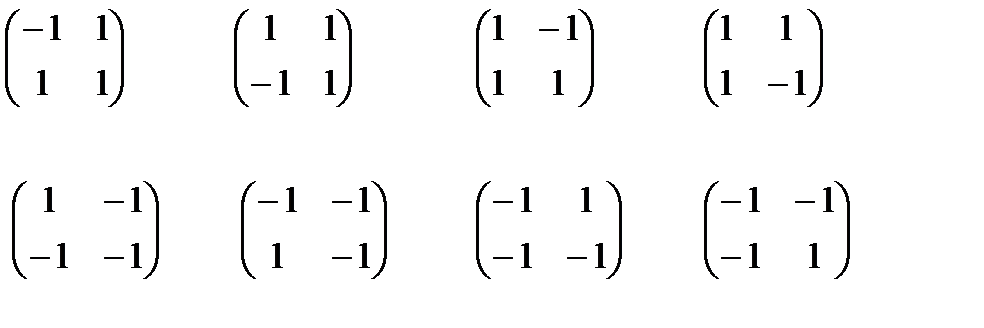(8.9)

(8.10)

являются матрицами Адамара, т.к. они удовлетворяют условию

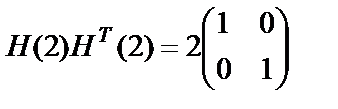. (8.11)

При возведении в кронекеровы степени любой из матриц (8.9, 8.10) вновь получаются матрицы Адамара Н(n), удовлетворяющие условию:

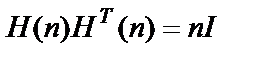, (8.12)

где I – диагональная единичная матрица размерности n:

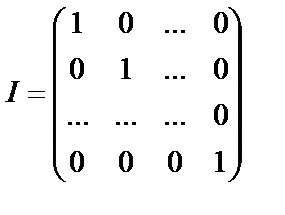. (8.13)

Например,

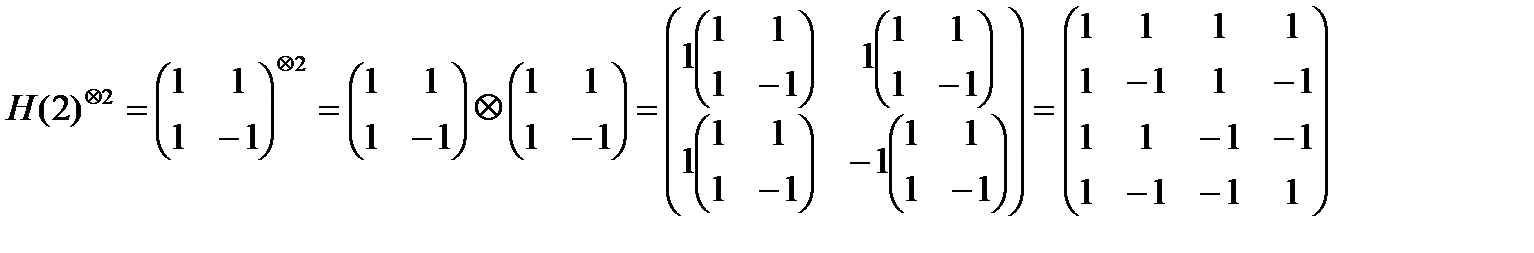, (8.14)

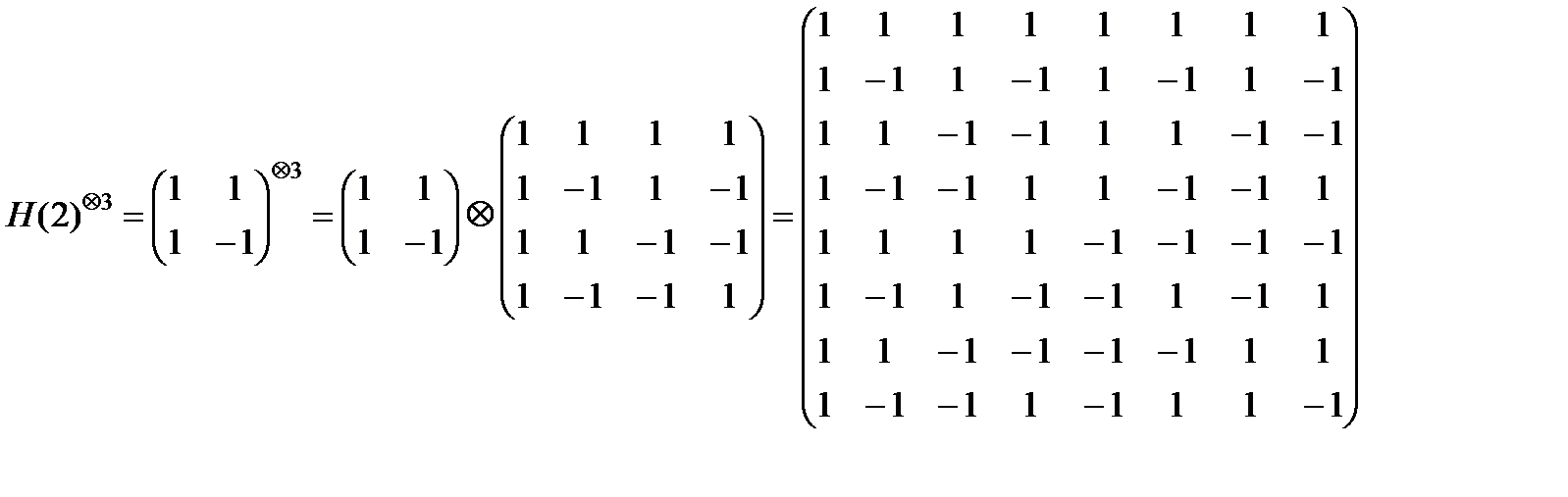(8.15)

и так далее по алгоритму

Н(2)^Äk = Н(2^k) = Н(2)Ä Н(2)^Äk-1 = Н(2)Ä Н(2^k-1), (8.16)

Благодаря различным уникальным свойствам матрицы Адамара Н(n) получили широкое применение во многих областях науки. В теории кодирования матрицы Н(n) используют для разработки помехоустойчивых кодов с исправлением ошибок, в теории планирования они применяются для составления блок-схем. Матрицы Адамара оказались полезными для расшифровки генетического кода, т. е. для изучения спиральной структуры молекулы ДНК.

5. «База», показанная на рис. 8.1, выбрана условно. В случае выбора другой «базы» из 4-базисов, показанных на рис. 6.3, знаки в матрице стигнатур (8.2) поменяются местами, но ее свойства не изменятся. С этим видом инвариантности связаны отдельные свойства l_m¸n -вакуума, которые будут рассмотрены позже.

6. Шестнадцати 4-базисам, приведенным на рис. 6.3 и в табл. 8.1, соответствуют 16 типам «цветных» кватернионов (8.17)

z1 = x0 + ix1 + jx2 + kx3 {+ + + +}   z2 = –x0 –ix1 – jx2+ kx3 {– – – +}   z3 = x0 – ix1 – jx2+ kx3 {+ – – +}   z4 = –x0 – ix1+ jx2–kx3 {– – + –}   z5 = x0 +ix1 – jx2 –kx3 {+ + – –}   z6 = –x0 + ix1 – jx2–kx3 {– + – –}   z7 = x0 – ix1+ jx2 – kx3 {+ – + –}   z8 = –x0+ix1 + jx2 + kdx3 {– + + +}

{– – – –} z9 = –x0 – ix1 – jx2 – kx3   {+ + + –} z10 = x0 + ix1 + jx2 – kx3   {– + + –} z11= – x0 + ix1 + jx2 – kx3   {+ + – +} z12= x0 + ix1 – jx2 + kx3   {– – + +} z13= –x0 – ix1 + jx2+ kx3   {+ – + +} z14= x0 – ix1 +jx2+ kx3   {– + – +} z15 = –x0 + ix1– jx2+ kx3   {+ – – –} z16 = x0 – ix1 – jx2 – kx3

В [2] показано, что «цвета» кватернионов соответствуют «цветам» квантовой хромодинамики.

Прямым вычислением легко убедиться, что сумма всех 16 типов «цветных» кватернионов (8.17) равна нулю

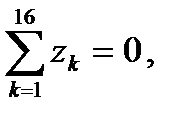(8.18)

т. е. суперпозиция всех типов «цветных» кватернионов сбалансирована относительно нуля.

В теории спиноров кватернионы являются одним из разновидностей клиффордовых агрегатов [16]:

а = а₀ + e₁а₁ + e₂а₂ + e₃а₃, (8.19)

где а_i – вещественные числа; e_i – орты, подчиняющиеся правилу умножения

1e_i=е_i1, e_ie_k= – d_ik 1 + e_ikne_n, (8.20)

где d_ik и e_ikn – символы Кронекера и Леви-Чивиты (i, k, n = 1,2,3).

7. Матрица стигнатур (8.2) может быть представлена в виде суммы диагональной и антисимметричной матриц

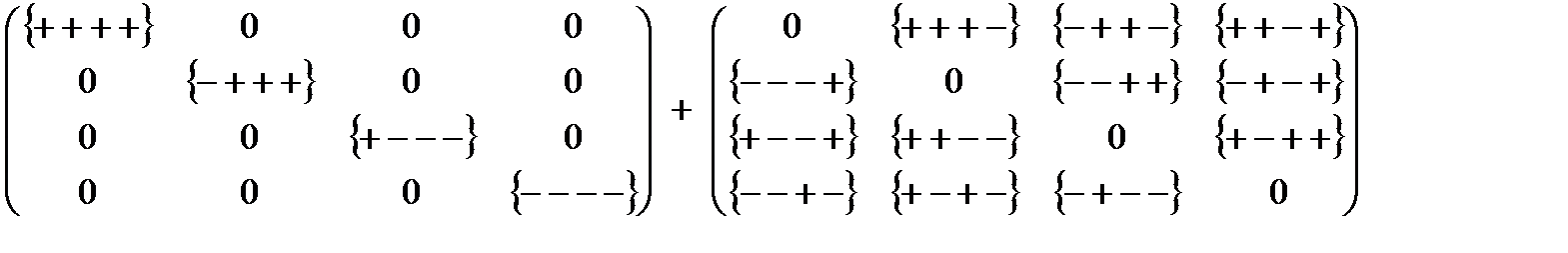(8.21)

8. Пусть задана матрица, составленная из четырех элементов a, b, c, d

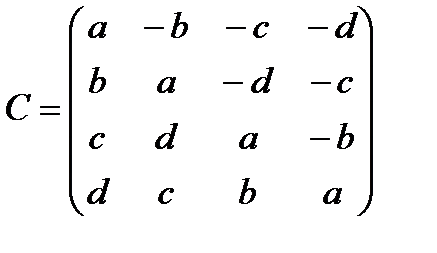, (8.22)

Произведение матрицы (8.22) с одной из матиц Адамара (8.14) приводи к матице, компонентами которой являются линейные формы с различными стигнатурами (8.23)

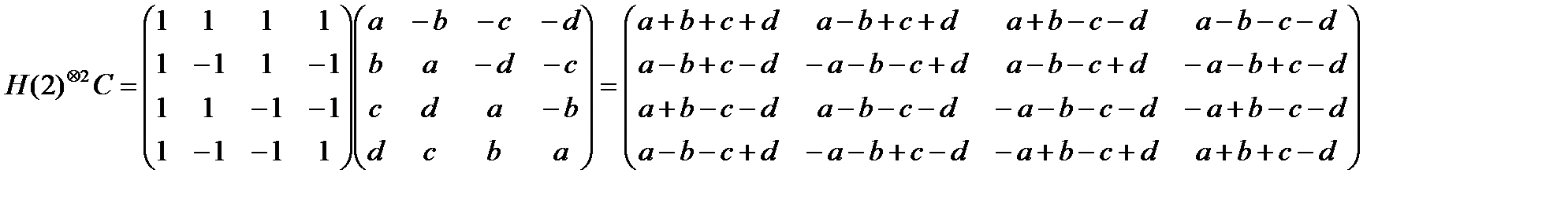
Алгебра сигнатур

Перейдем от аффинных геометрий к метрическим. Для примера рассмотрим аффинное (векторное) пространство с 4-базисом e_i⁽⁷⁾(e₀⁽⁷⁾,e₁⁽⁷⁾,e₂⁽⁷⁾,e₃⁽⁷⁾) (рис. 6.3) со стигнатурой {+ + + –}.

Зададим в этом пространстве 4-вектор

ds⁽⁷⁾ = e_i⁽⁷⁾dx_i⁽⁷⁾ = e₀⁽⁷⁾dx₀⁽⁷⁾+e₁⁽⁷⁾dx₁⁽⁷⁾+e₂⁽⁷⁾dx₂⁽⁷⁾+e₃⁽⁷⁾dx₃⁽⁷⁾, (10.1)

а) {+ + + +} б) {+ + + –} Рис. 10.1. Два 4-базиса с различными стигнатурами

где dx_i⁽⁷⁾ – это i-я проекция 4-вектора ds⁽⁷⁾ на ось x_i⁽⁷⁾, направление которой определяется базисным вектором e_i⁽⁷⁾.

Рассмотрим другой 4-вектор (10.2)

ds⁽⁵⁾ = e_i⁽⁵⁾dx_i⁽⁵⁾= e₀⁽⁵⁾dx₀⁽⁵⁾+e₁⁽⁵⁾dx₁⁽⁵⁾+e₂⁽⁵⁾dx₂⁽⁵⁾+ e₃⁽⁵⁾dx₃⁽⁵⁾,

заданный в аффинной системе отсчета x₀⁽⁵⁾, x₁⁽⁵⁾, x₂⁽⁵⁾, x₃⁽⁵⁾ с 4-базисом e_i⁽⁵⁾ (e₀⁽⁵⁾, e₁⁽⁵⁾, e₂⁽⁵⁾, e₃⁽⁵⁾) (рис. 6.3), со стигнатурой {+ + + +}.

Найдем скалярное произведение 4-векторов (10.1) и (10.2)

ds^{(5,7) 2} = ds⁽⁵⁾ds⁽⁷⁾ = e_i⁽⁵⁾e_j⁽⁷⁾dxⁱ dx^j = (10.3)

=e₀⁽⁵⁾e₀⁽⁷⁾dx₀dx₀ + e₁⁽⁵⁾e₀⁽⁷⁾dx₁dx₀ + e₂⁽⁵⁾e₀⁽⁷⁾dx₂dx₀ + e₃⁽⁵⁾e₀⁽⁷⁾dx₃dx₀ +

+ e₀⁽⁵⁾e₁⁽⁷⁾dx₀dx₁ + e₁⁽⁵⁾e₁⁽⁷⁾dx₁dx₁ + e₂⁽⁵⁾e₁⁽⁷⁾dx₂dx₁ + e₃⁽⁵⁾e₁⁽⁷⁾dx₃dx₁ +

+e₀⁽⁵⁾e₂⁽⁷⁾dx₀dx₂ + e₁⁽⁵⁾e₂⁽⁷⁾dx₁dx₂ + e₂⁽⁵⁾e₂⁽⁷⁾dx₂dx₂ + e₃⁽⁵⁾e₂⁽⁷⁾dx₃dx₂ +

+e₀⁽⁵⁾e₃⁽⁷⁾dx₀dx₃ + e₁⁽⁵⁾e₃⁽⁷⁾dx₁dx₃ + e₂⁽⁵⁾e₃⁽⁷⁾dx₂dx₃ + e₃⁽⁵⁾e₃⁽⁷⁾dx₃dx₃.

Для рассматриваемого случая, скалярные произведения базисных векторов e_i⁽⁵⁾e_j⁽⁷⁾ равны:

при i = j e₀⁽⁵⁾e₀⁽⁷⁾ = 1, e₁