Общие сведения о колебаниях.

КОЛЕБАНИЯ И ВОЛНЫ

Учебное пособие

Pостов-на-Дону 2009

УДК 530.1

С 74

Авторы: Егорова С.И., Егоров И.Н., Кунаков В.С., Лемешко Г.Ф., Наследников Ю.М.

Колебания и волны: Учеб. пособие.- Ростов н/Д: Изда­тельский центр ДГТУ,2009.- 55 с.

В данном пособии рассматривается теория механических и электрических колебаний как единый процесс. Колебания излагаются в рамках модели одномерного гармонического осциллятора.

Учебное пособие (включая электронную версию) предназначено для студентов, изучающих физику, для самостоятельной работы в период подготовки к рейтинговому контролю и экзамену, а также при подготовке к лабораторным работам.

Печатается по решению редакционно-издательского совета

Донского государственного технического университета.

Научный редактор д-р техн. наук, проф. Кунаков В.С..

© Егорова С.И., Егоров И.Н., Кунаков В.С.

Лемешко Г.Ф., Наследников Ю.М.

.

© Издательский центр ДГТУ, 2009

Предисловие

Учебное пособие составлено в соответствии с рабочей программой по физике. Оно не может и не должно заменить учебник и предназначено для того, чтобы помочь студентам при подготовке к лабораторным работам и экзаменам.

Колебания излагаются в рамках модели одномерного гармонического осциллятора. Тем самым задаётся общий подход к теории колебаний различной физической природы.

Для упрощения вывода решения дифференциального уравнения затухающих колебаний введён энергетический подход к рассеянию энергии.

Решение дифференциального уравнения вынужденных колебаний проводится геометрически через векторные диаграммы, что позволяет избежать сложных математических выкладок.

При рассмотрении автоколебаний особое внимание уделяется выделению основных элементов автоколебательной системы.

Общая теория колебаний позволяет студентам осознать значимость теории колебаний не только в физике и технике, но и в понятии цикла, как основы мироздания.

Общие сведения о колебаниях.

Сложение колебаний

Векторная диаграмма

Гармонические колебания удобно представлять в виде векторных (круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора, равного по модулю амплитуде колебаний .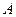

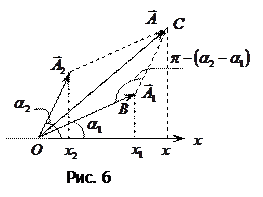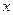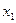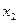Воспользуемся методом векторных диаграмм при сложении гармонических колебаний одинакового направления с одинаковыми частотами. Смещение колеблющегося тела равно сумме смещений и , которые записываются следующим образом:

и (16)

Представим оба колебания с помощью векторов 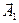и 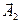(рис. 6). Построим по правилам сложения векторов результирующий вектор 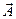. Легко видеть, что проекция этого вектора на ось 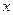равна сумме проекций слагаемых векторов 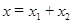. Следовательно, проекция вектора 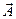представляет собой результирующее колебание.

Этот вектор вращается с той же угловой скоростью (циклической частотой) 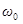, как и векторы 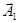и 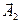, так что результирующее движение будет гармоническим колебанием с частотой 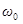, амплитудой 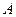и начальной фазой 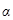. Из построения видно, что

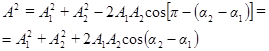(17)

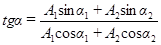. (18)

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения вращающихся векторов.

Проанализируем выражение (17) для амплитуды:

а) если разность фаз колебаний 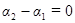, т.е. колебания происходят в одинаковой фазе, то амплитуда результирующего колебания равна ;

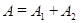б) если разность фаз колебаний 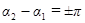, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания .

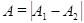Биения

Особый интерес представляет случай, когда два складываемых колебания одинакового направления малоотличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.

Пусть частота одного колебания 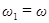, а частота второго колебания 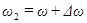, причем, . Амплитуды обоих колебаний полагаем одинаковыми и равными 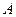. Для упрощения расчетов полагаем начальные фазы колебаний равными нулю. Тогда уравнения складываемых колебаний будут иметь следующий вид:

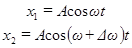
Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов 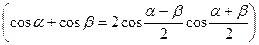, получаем 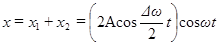(19).

(во втором множителе пренебрегли членом 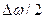по сравнению с ).

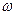График функции (19) для случая 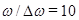изображен на рисунке 7.а.

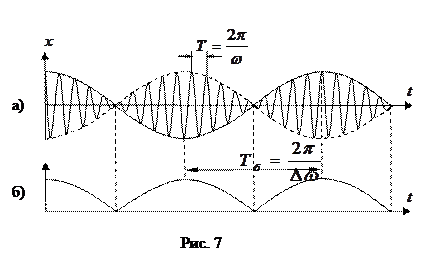Заключенный в скобки множитель в формуле (19) изменяется гораздо медленнее, чем второй множитель, так как . Это дает нам основание рассматривать колебание (19) как гармоническое колебание частоты 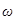, амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется от 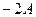до 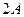, в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:

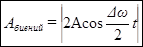. (20)

Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой 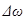. Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:

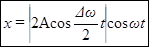(21)

Затухающие колебания.

Вынужденные колебания

Пусть колебательная система, например шарик на пружине, подвергается действию внешней силы, изменяющейся со временем по гармоническому закону:

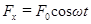. (45)

В этом случае уравнение второго закона Ньютона имеет вид:

.

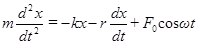Введя обозначения 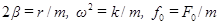, запишем это уравнение следующим образом:

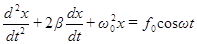. (46)

Мы получили неоднородное дифференциальное уравнение вынужденных колебаний. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем (см. функцию (40), являющуюся общим решением уравнения (32)):

,

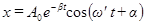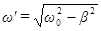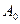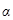где , и - произвольные постоянные.

Следует помнить, что это уравнение описывает затухающие колебания, которые представляют интерес только с точки зрения подхода к установившимся колебаниям. Нас же интересуют только установившиеся вынужденные колебания. Частное решение будем искать в виде:

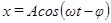. (47)

Воспользуемся помощью векторной диаграммы и метода подстановки решения (47) в исходное уравнение (46). При этом получаем:

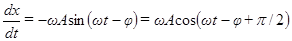; (48)

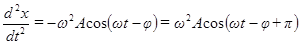. (49)

Подстановка выражений (47) - (49) в уравнение (46) приводит к соотношению:

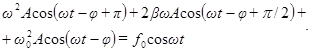(50)

Из (50) следует, что постоянные 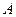и 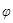должны иметь такие значения, чтобы гармоническая функция 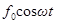была равна сумме трех гармонических функций, стоящих в левой части уравнения. Если изобразить функцию 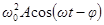вектором длиной 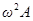, направленным вправо, то функция 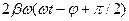изобразится вектором длиной 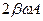(рис.13), повёрнутым относительно вектора 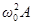против часовой стрелки на угол 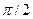, а функция 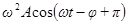- вектором длиной 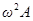, повернутым относительно вектора 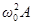на угол 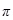. Для того, чтобы уравнение (50) было удовлетворено, сумма трех перечисленных векторов должна совпадать с вектором, изображающим функцию 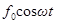. Из рисунка 13.a видно, что такое совпадение возможно лишь при значении амплитуды, которое определяется условием:

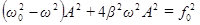, откуда

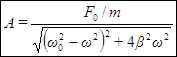. (51)

Мы заменили 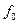отношением 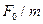. Рисунок отвечает случаю 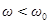. Из рисунка 13.б отвечающему случаю 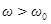получается такое же значение .

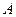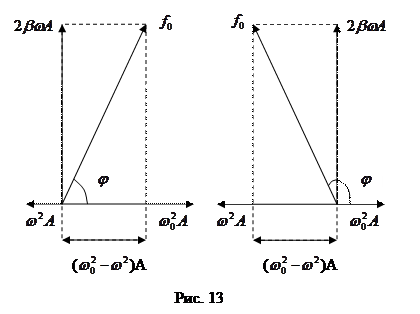
Рис. 13 позволяет получить также и значение 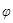, которое представляет собой величину отставания по фазе вынужденного колебания (47) от обусловившей его вынуждающей силы. Из рисунка видно, что

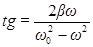. (52)

Подставив в (47) значения 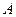из (51) и 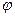из (52), получим функцию, являющуюся частным решением уравнения, описывающего установившиеся вынужденные колебания:

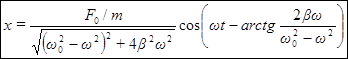. (53)

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда достигает максимального значения. Резкое возрастание амплитуды колебаний называется резонансом, а соответствующая частота, при которой амплитуда достигает максимального значения, называется резонансной частотой. .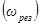

Для определения резонансной частоты нужно найти максимум функции (51) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по 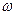и приравняв нулю, мы получим условие, определяющее резонансную частоту:

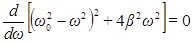
(54)

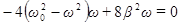
Уравнение (54) имеет три решения: 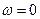и .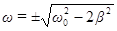

Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение.

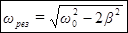(55)

Подставив это значение частоты в (51), получим выражение для амплитуды при резонансе

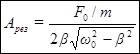(56)

Из (56) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (55) резонансная частота при тех же условиях (при 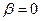) совпадает с собственной частотой колебания системы .

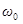Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) показана на рис. 14.

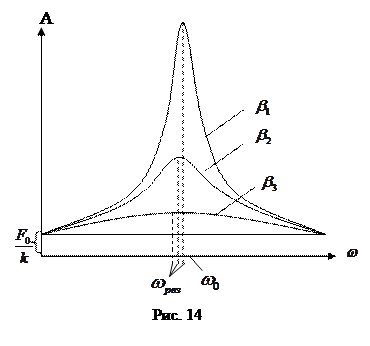
Отдельные кривые на графике соответствуют различным значениям параметра 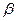. В соответствии с (55) и (56), чем меньше 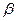, тем выше и правее лежит максимум данной кривой. При очень большом затухании (когда 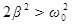) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 14). Изображенная на рис. 14 совокупность графиков функций (56), соответствующих различным значениям параметра 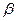, называется резонансными кривыми.

По поводу резонансных кривых можно сделать ещё следующие замечания. При стремлении 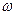к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному 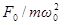, т.е. 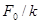. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы 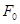. При стремлении 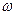к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет своё направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше 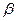, тем сильнее изменится с частотой амплитуда вблизи резонанса, тем острее получается максимум.

Из формулы (56) вытекает, что при малом затухании (т.е. при 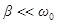) амплитуда при резонансе приближенно равна

.

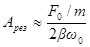Разделим это выражение на смещение 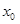от положения равновесия под действием постоянной силы 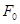, равной 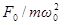. В результате получим:

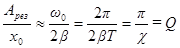(57)

Таким образом, добротность показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).

Из рис. 13 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания 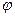лежит в пределах от 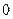до .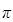

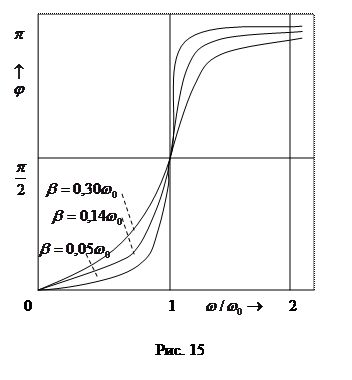
Зависимость 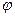от 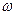при различных значениях 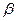показана графически на рис. 15. Частоте 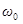соответствует 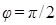. Из (55) видно, что резонансная частота меньше собственной. Следовательно, в момент резонанса 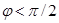. При слабом затухании 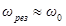и значение 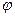при резонансе можно считать равным .

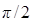С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних взаимодействий. Например, собственная вибрация корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае возникают вибрации, которые могут вызвать катастрофу. Известны случаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебания моста была близка к частоте, с которой шагала колонна.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике, и т.д.

Автоколебания.

Параметрический резонанс

Автоколебанияминазываются незатухающие колебания, обусловленные управляемым самой системой пополнением энергии от источника неколебательной природы. Любая автоколебательная система состоит из четырёх частей: колебательной системы, источника энергии неколебательной природы, клапана, регулирующего поступление энергии в колебательную систему, определенными порциями, обратной связи или устройства управления работой клапана за счет процессов в самой колебательной системе.

Обратная связь называется положительной (отрицательной), если в течение времени воздействия источника энергии на колебательную систему источник энергии производит над системой положительную (отрицательную) работу и передает ей (отнимает от нее) некоторый запас энергии. Положительная обратная связь используется для возбуждения автоколебаний. В случае отрицательной обратной связи усиливается затухание, и автоколебания подавляются.

Автоколебательными системами являются, например, часы, паровые машины и двигатели внутреннего сгорания, отбойные молотки, электрические звонки. Автоколебания совершают струны под действием смычка в скрипке, воздушные столбы в трубах духовых инструментов, язычки в баянах и аккордеонах, голосовые связки при разговоре или пении. Электрической автоколебательной системой является генератор незатухающих электрических колебаний. В ряде случаев механизм обратной связи автоколебательной системы замаскирован, и разбиение системы на основные части затруднительно.

В качестве примера автоколебательной системы рассмотрим часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом – анкером. На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо опирается на один из зубьев в боковую поверхность той или иной палетты, скользящей при качании маятника по поверхности зуба. Только в момент, когда маятник находится вблизи среднего положения, палетты перестают преграждать путь зубьям, и ходовое колесо поворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качания маятника (период) ходовое колесо проворачивается на два зуба, причем каждый из палетт получает по толчку. Посредством этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения. Итак, в часах колебательной системой является маятник. Источником энергии – поднятая вверх гиря или заведенная пружина. Клапаном является анкер. Обратная связь осуществляется взаимодействием анкера с ходовым колесом.

Существует еще один вид взаимодействия извне, с помощью которого можно сильно раскачать систему. Этот вид взаимодействия заключается в совершаемом в такт с колебаниями периодическом изменении какого-либо параметра системы, вследствие чего само явление называется параметрическим резонансом.

Возьмем для примера простейший маятник – шарик на нитке. Если периодически изменять длину маятника, увеличивая её в моменты, когда маятник находится в крайнем положении, и, уменьшая в моменты, когда маятник находится в среднем положении (рис. 16), то маятник сильно раскачается. Увеличение энергии маятника при этом происходит за счет работы, которую совершает сила, действующая на нить. Сила натяжения нити при колебаниях маятника непостоянна: она меньше в крайних положениях, когда скорость обращается в ноль, и больше в среднем положении, когда скорость маятника максимальна. Поэтому отрицательная работа внешней силы при удалении маятника оказывается меньше по величине, чем положительная работа, совершаемая при укорочении маятника. В итоге работа внешних сил за период оказывается больше нуля.

Переменный ток

Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей электроёмкостью, индуктивностью и активным сопротивлением, переменного тока. Под действием внешнего напряжения

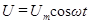,где(101)

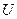- мгновенное значение напряжения, 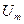- амплитуда напряжения.

Ток в цепи изменяется по закону

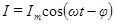, где (102)

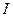- мгновенное значение силы тока, 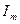- амплитуда силы тока.

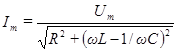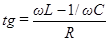, (103)

Полученное выражение для амплитуды силы тока можно толковать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой 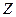и называют полным сопротивлением или импедансом:

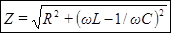. (104)

Видно, что при 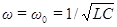это сопротивление минимально и равно активному сопротивлению 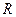. Величину, стоящую в круглых скобках формулы (104), обозначают буквой 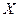и называют реактивным сопротивлением:

,

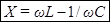где 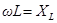- индуктивное сопротивление,

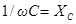- ёмкостное сопротивление.

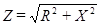(106)

Заметим, что индуктивное сопротивление растёт с увеличением частоты, а ёмкостное – уменьшается. Когда говорят, что в цепи отсутствует ёмкость, то это надо понимать в смысле отсутствия ёмкостного сопротивления, которое равно 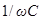и, следовательно, обращается в нуль, если 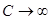(при замене конденсатора закороченным участком).

Реактивное сопротивление измеряют в тех же единицах, что и активное, но между ними существует принципиальное различие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту.

Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:

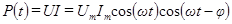(107)

Воспользовавшись формулой

,

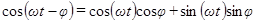преобразуем (107) к виду

.

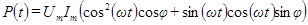Практический интерес имеет среднее за период колебания значение мощности. Учитывая, что средние значения 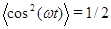, а 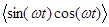= 0 , получим

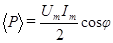(108)

Это выражение можно привести к другому виду, если принять во внимание, что из векторной диаграммы (рис 21) следует, что 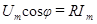, поэтому

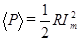(109)

Такую же мощность развивает постоянный ток .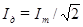

Величины

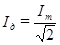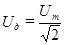, (110)

называютдействующими (эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуированы по действующим значениям тока и напряжения.

Выражение средней мощности (108) через действующие значения силы тока и напряжения имеет вид:

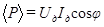(111)

Входящий в это выражение множитель 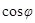называется коэффициентом мощности. В технике стремятся сделать 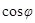как можно большим. При малом 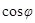для выделения в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.

Упругие волны

Упругими (механическими) волнами называются механические возмущения, распространяющиеся в упругой среде.

Упругие волны бывают продольными(в которых частицы среды колеблются в направлении распространения волны) и поперечными (в которых частицы колеблются в плоскостях, перпендикулярных направлению распространения волны).

Внутри жидкостей и в газах возникают только продольные волны, в твёрдых телах – продольные и поперечные.

Длиной волны называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе

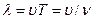,(112)

где 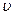- скорость волны, 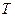- период, 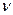- частота.

Уравнение бегущей волны

Бегущими называются волны, которые переносят в пространстве энергию.

Распространение волн в однородной изотропной среде в общем

случае описывается волновым уравнением:

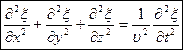, (113)

которое является дифференциальным уравнением в частных производных.

Здесь 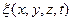- смещение колеблющейся частицы, как функция координат и времени, 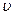-фазовая скорость, т.е. скорость перемещения фазы колебаний.

Для плоской волны волновое уравнение имеет вид:

.

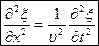Решение этого уравнения является уравнением бегущей плоской

волны, распространяющейся вдоль положительного направления оси 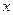в

среде, не поглощающей энергию:

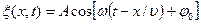или

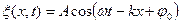, (114)

где 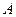- амплитуда волны, 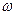- циклическая частота, 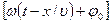-фаза волны, 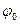- начальная фаза, 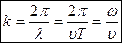- волновое число, 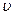-фазовая скорость.

Стоячие волны

Особым случаем интерференции являются стоячие волны – это волны, образующиеся при наложении двух волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу.

Такой случай можно реализовать, заставив бегущую волну отразиться от преграды (рис. 24).

Уравнения падающей и отражённой волн имеют вид:

.

Сложив эти уравнения, используя тригонометрические преобразования, получаем уравнение стоячей волны:

, (119)

где амплитуда стоячей волны:

. (120)

Из выражения (120) видно, что амплитуда стоячей волны

. (121)

Точки, в которых амплитуды бегущей и отражённой волны складываются, называются пучностями( ).

Точки, в которых амплитуда равна нулю, называются узлами( ). Эти точки колебаний не совершают.

Пучность образуется в тех точках, где колебания бегущей и отражённой волн происходят в одинаковой фазе, т.е. ( ). Следовательно, координаты пучностей:

( ) . (122)

Узлы образуются там, где колебания происходят в противофазах, т.е. ( ). Следовательно, координаты узлов:

( ). (123)

Длиной стоячей волны называется расстояние между пучностями или узлами: .

Таким образом, длина стоячей волныравна половине длины складываемых волн:

. (124)

Стоячая волна не переносит энергии, т.к. энергия переносится в равных количествах бегущей и отражённой волнами.

Электромагнитные волны

Из уравнений Максвелла вытекает существование электромагнитных волн– переменного электромагнитного поля, распространяющегося в вакууме с конечной скоростью .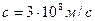

Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряжённостей электрического и магнитного полей удовлетворяют уравнениям:

(124)

(125)

где 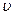- фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (124) и (125), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением

, (126)

где - скорость электромагнитной волны в вакууме, , - электрическая и магнитная постоянные, , - диэлектрическая и магнитная проницаемости среды, - показатель преломления среды.

В вакууме ( ) , . Поскольку скорость электромагнитной волны в среде всегда меньше, чем в вакууме, т.е. .

Длина электромагнитной волны

.

Следствием теории Максвелла является поперечность электромагнитных волн: векторы и взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости распространения волны, причём векторы , и образуют правовинтовую систему (рис. 25). Из уравнений Максвелла следует также, что в электромагнитной волне векторы и всегда колеблются в одинаковых фазах, причём мгновенные значения напряжённостей электрического и магнитного полей электромагнитной волны в любой точке связаны соотношением:

. (127)

Источником электромагнитных волн может быть любой колебательный контур или проводник, по которому течёт переменный ток. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объём пространства, в котором электромагнитное поле создаётся. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры (рис. 17), т.к. в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки индуктивности.

Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стержня, разделённых искровым промежутком. Колебания в такой системе поддерживаются за счёт источника э.д.с., подключённого к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объёмная плотность энергии электромагнитной волны равна сумме плотностей энергий электрического и магнитного полей:

. (128)

Учитывая выражение (127), получим, что плотности электрического и магнитного полей в каждый момент времени одинаковы, т.е. . Поэтому

Умножив плотность энергии на скорость распространения волны в среде из формулы (126), получим плотность потока энергии, т.е. энергию, переносимую волной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению распространения волны:

.

Так как вект<