Определение коэффициента теплопроводности

Твердых тел

Цель работы: определить коэффициент теплопроводности диэлектрика.

Методика эксперимента

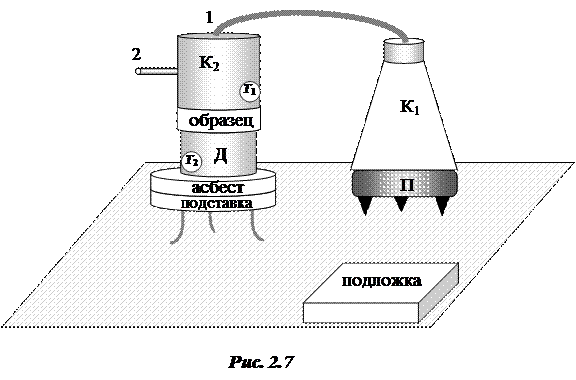
Эксперимент проводится на установке (рис 2.7), состоящей из плитки П, колбы К₁ с водой, коробки К₂ с тремя отверстиями: 1 и 2 для подвода и отвода пара и третье - для термометра Т₁. Под сосудом К₂ находится исследуемый образец, лежащий на стальном диске Д, принимающим тепло, прошедшее через образец. Диск Д имеет отверстие для термометра Т₂.

Коэффициент теплопроводности l определяется по скорости охлаждения образца. Тепло, подведенное к диску Д за время Dt, равно количеству теплоты, перенесенному через образец. Это положение и используется при определении коэффициента теплопроводности неметаллического образца, слабо проводящего тепло.

Количество теплоты, излучаемое диском:

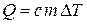(2.24)
где c – удельная теплоемкость вещества; m – масса образца; DТ – разность конечной и начальной температур (DТ = Т₂ - Т₁).

Преобразуем (2.24), введя скорость охлаждения :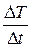

,
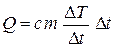где Dt – время излучения.

При удаленном образце (слабо проводящем тепловое излучение), излучающей поверхностью диска является его полная поверхность S₁ (два основания и боковая поверхность):

,

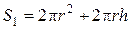где r – радиус диска; h – толщина диска.

При этом поток излучения 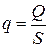будет равен

.

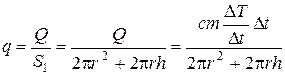Убранный на теплоизолирующую подложку при установившейся температуре Т₂, диск Д излучает только с поверхности S₂ (одно основание и боковая поверхность), то есть с той же поверхности, что и при контакте с образцом

.

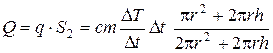Проведя преобразования и учитывая, что D = 2r, получим:

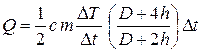. (2.25)

Если концы твердого тела поддерживаются при разных температурах, то некоторое количество теплоты Q переносится от более нагретой части тела к менее нагретой.

Согласно закону Фурье

,
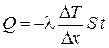где l - коэффициент теплопроводности данного вещества; 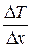- градиент температуры (DТ = Т₂ – Т₁); S – площадь сечения образца; t – время.

В нашем случае площадь сечения образца равна 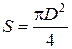, тогда формула (2.41) приобретает вид:

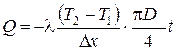. (2.26)

Основываясь на том, что количество тепла, полученное диском Д, равно количеству тепла, потерянному поверхностью S₂ при температуре Т₂ (по модулю), приравниваем модули выражений (2.25) и (2.26):

.

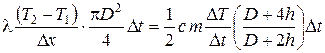Из последнего равенства получаем расчетную формулу для определения коэффициента теплопроводности исследуемого образца:

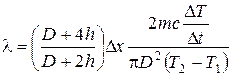. (2.27)

Порядок выполнения работы

1. Включить в сеть нагреватель (плитку) П сосуда с водой (см. рис. 2.7).

2. Провести однократные измерения толщины исследуемого образца Dx, диаметра D и толщины h стального диска.

3. Довести воду в сосуде до кипения, пропускать пар в коробку К₂ до тех пор, пока температуры коробки Т₁ и диска Т₂ не перестанут изменяться.

4. Результаты измерений и постоянные установки занести в таблицу 2.5.

Таблица 2.5

D	h	Dx	T1	T2	Параметры
					m = кг (масса диска) с = 460 Дж/кг×К (удельная теплоемкость диска)

5. Удалить коробку К₂ и образец со стального диска, поместив диск на подложку.

6. Через равные промежутки времени Dt = 2 мин измерять температуру Т при охлаждении диска. Результаты измерений занести в таблицу 2.6.

Таблица 2.6

t,мин	Т,°С	t,мин	Т,°С

7. Построить график зависимости T = f(t).

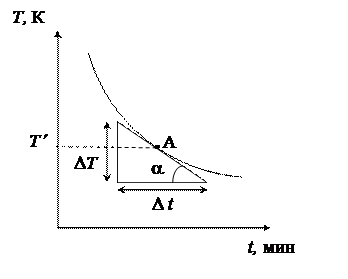Пример нахождения скорости охлаждения

Выберем на графике точку А. Ей соответствует некоторая температура Т¢. Скорость охлаждения 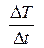представляет собой тангенс угла a наклона касательной в данной точке.

8. Построить касательную к произвольной точке графика T = f (t). Взять ее произвольный отрезок и построить треугольник с катетами DТ и Dt. Найти отношение 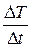- скорость охлаждения образца.

9. По формуле (2.27) рассчитать коэффициент теплопроводности.

10. Сравнить результат экспериментального определения коэффициента теплопроводности с табличным значением.

11. Сделать вывод по проделанной работе.

Контрольные вопросы и задания

1. Объясните механизм переноса тепла (теплопроводности).

2. Запишите и объясните закон Фурье.

3. Каков физический смысл коэффициента теплопроводности?

4. В каких единицах измеряется коэффициент теплопроводности?

Термодинамика

Молекулярно-кинетическая теория газов объясняет макроскопические свойства веществ путем детального разбора тех процессов, которые происходят на молекулярном уровне, и макроскопические величины имеют какие-то определенные значения лишь потому, что они являются средними значениями огромного числа отдельных элементарных процессов. Метод, который применяется при этом, – статистический метод.

Однако существует и другой способ описания тех же явлений. Такое описание возможно, если рассматривать их с позиции превращения одних видов энергии в другие. Этот раздел физики носит название«термодинамика». Термодинамика не входит в рассмотрение микроскопических процессов, но так же как молекулярно-кинетическая теория газов позволяет делать целый ряд выводов относительно их протекания. Законы, лежащие в основе термодинамики, с успехом применяются для исследования и физических, и химических процессов, для изучения свойств веществ и излучения. Основу термодинамики образуют два ее начала и тепловой закон Нернста (или третье начало термодинамики).

Первые два начала термодинамики позволяют:

· устанавливать количественные соотношения, имеющие место при превращениях энергии из одних видов в другие (первое начало);

· определять условия, при которых возможны эти превращения, и определять возможные направления процессов (второе начало).