Равновесие тела под действием плоской системы сл

Общий подход к решению задачи об определении реакций опор

Во многих случаях, встречающихся в инженерной практике, заранее известно, что некоторое тело находится в равновесии. Например, оно соответствующим образом закреплено (имеет опоры). На тело действуют заданные силы, которые называют активными. Природа активных сил, как правило, не указывается, т.е. неважно какие тела и по каким физическим законам взаимодействуют с рассматриваемым телом, дан только результат этого взаимодействия в виде сил. Под действием активной нагрузки тело оказывает давление на опоры (связи), со стороны которых, в соответствии с третьим законом Ньютона, возникают реакции связей. Задача состоит в определении сил реакций связей.

Сила реакции связи заранее неизвестна, она зависит от приложенных к телу активных сил и вида самой связи. Заранее можно только утверждать, что сила реакции связи направлена в сторону, противоположную той, куда данная связь не даёт перемещаться телу.

При решении задач об определении сил реакций опор предлагается следующая последовательность действий.

1. Проведя сечение по соответствующим связям, выбрать тело (или систему тел), равновесие которого будет рассматриваться и изобразить на чертеже приложенную к выбранному телу активную нагрузку.

2. Ввести реакции связей, изобразив силы реакций на чертеже. Если направление сил реакций заранее неизвестно, необходимо показать их составляющие.

3. Составить условия равновесия для системы сил, приложенной к рассматриваемому телу и определить неизвестные. Эта система сил состоит из всех активных сил и всех реакций внешних связей.

4. Из составленных уравнений определить неизвестные величины.

Условия равновесия системы сил, линии действия которых расположены в одной

Плоскости

В дальнейшем на лекциях будет показано, что

Для равновесия системы сил, линии действия которых расположены в одной плоскости, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух взаимно перпендикулярных осей, лежащих в плоскости действия сил, равнялась нулю и сумма моментов всех сил относительно оси, перпендикулярной плоскости действия сил, равнялась нулю

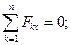
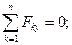
(1.1)

где 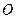– произвольно выбранная точка плоскости .

В курсе статики используется, в основном, декартова система координат, три взаимно перпендикулярных оси которой – , имеют орты .

Первые два уравнения равновесия (1.1) связывают проекции векторов сил на выбранные координатные оси. Чтобы построить такую проекцию, нужно перенести ось параллельно самой себе так, чтобы она проходила через точку приложения силы и опустить перпендикуляры на ось из начала и конца вектора (Рис. 1.1-1.2):

проекцией вектора 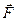на координатную ось 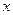называется взятая с соответствующим знаком длина отрезка оси, заключённого между проекциями начала и конца вектора

Рис. 1.1		Рис. 1.2

Таким образом, ортогональная проекция вектора силы 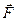на ось 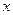определяется по формуле

где – модуль силы; 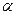– острый угол между двумя прямыми: линией действия вектора 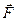и осью .

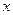При этом проекция положительна, если условное перемещение от проекции начала вектора к проекции его конца совпадает с положительным направлением оси 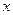и отрицательна в противоположном случае.

Третье уравнение (1.1) связывает так называемые моменты сил. Рассмотрим некоторую пластину, которая может вращаться вокруг оси , проходящей через закреплённую точку 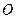перпендикулярно плоскости пластины (Рис. 1.3). К пластине приложены две силы,

Рис. 1.3

которые стремятся вращать пластину в противоположные стороны. Куда будет вращаться пластина? Опыт показывает, что вращательный эффект силы зависит не только от её величины, но и от её расположения по отношению к оси. Вращательный эффект силы характеризует её момент относительно оси :

где – плечо силы, равное кратчайшему расстоянию от точки 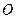до линии действия силы; знак « + » соответствует повороту вокруг точки 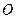против хода часовой стрелки.

Напомним, что мы говорим о силах, линии действия которых расположены в плоскости, перпендикулярной оси . В дальнейшем будут введены общие понятия момента силы относительно точки и оси.

Основные виды связей

Помимо заданных – активных сил – на тело, равновесие которого рассматривается, действуют силы, приложенные со стороны опор – связей. Реакция связи потому так и называется потому, что возникает в ответ – реагирует на действие сил, приложенных к телу. В зависимости от устройства связи обладают различными возможностями по ограничению перемещения точки закрепления.

Рассмотрим некоторые из так называемых идеальных связей. Понятие идеальных связей – важнейшее понятие механики будет подробно рассмотрено в дальнейшем при изучении аналитической механики. Пока будем считать связь идеальной, если возможно не учитывать явление трения.

Одна из самых распространённых опор – неподвижный цилиндрический шарнир (подшипник).Простейшую схему такой опоры можно представить следующим образом: имеется закреплённый стержень, на который надета пластина (Рис. 1.4). Такая опора позволяет пластине скользить вдоль стержня и вращаться вокруг него. Под действием активной нагрузки возникает точечный контакт между стержнем и пластиной. Реакция направлена по нормали к стержню (оси шарнира), но заранее неизвестно в какой точке осуществляется контакт и, следовательно, по какой из нормалей к оси шарнира будет направлена реакция.

Рис. 1.4		Рис.1.5

Таким образом, в общем случае реакция неподвижного шарнира расположена в плоскости, перпендикулярной оси шарнира, но в этой плоскости она заранее неизвестна ни по модулю, ни по направлению. Для её определения удобно ввести две неизвестные по модулю составляющие, направленные параллельно координатным осям в положительном направлении этих осей и . Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные оси и .

Размерами шарнира при расчётах пренебрегают. Схематическое изображение неподвижного шарнира представлено на Рис. 1.5. Конструктивно неподвижный цилиндрический шарнир, как правило, представляет собой шарикоподшипник.

Для некоторых видов опор перемещения точки закрепления ограничиваются только в определённом направлении. По этому направлению и действует сила реакции связей. В качестве неизвестной величины для опор такого типа имеет смысл рассматривать модуль реакции опоры.

Рассмотрим опоры, относящиеся к такому типу.

Гибкая невесомая нерастяжимая нить. Нить не даёт телу перемещаться в единственном направлении – вдоль нити от точки закрепления (на растяжение нити). Реакция такой нити 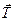всегда направлена вдоль нити к точке подвеса (Рис.1.6).

Рис. 1.6		Рис. 1.7

Гладкая (без трения) поверхность. Реакция такой поверхности направлена по общей нормали к поверхностям тел, проведённой в точке контакта, причём наружу от опорной поверхности (Рис.1.7а). Если в точке контакта у одной из поверхностей нормаль не определена (Рис.1.7б), то реакция направлена по нормали к другой поверхности.

Невесомый ненагруженный стержень с шарнирно закреплёнными концами.Пусть тело закреплено при помощи неподвижного шарнира 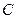и невесомого стержня 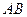, шарнирно закреплённого на концах (Рис. 1.8).

Рассмотрим стержень 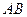(Рис.1.9). Он находится в равновесии под действием двух сил, приложенных в точках и . Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стержень 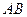направлена вдоль стержня. Учитывая третий закон Ньютона, приходим к выводу, что реакция ненагруженного стержня направлена вдоль прямой, соединяющей шарнирно закреплённые концы стержня.

Рис. 1.8		Рис. 1.9.

Схематическое изображение такой опоры и её реакция представлены на Рис.1.10.

Подвижный цилиндрический шарнир представляет собой цилиндрический шарнир, поставленный на катки, на которых он может без сопротивления перемещаться по опорной поверхности. Реакция направлена по нормали к опорной поверхности (Рис.1.11).

Рис.1.10		Рис.1.11		Рис.1.12		Рис.1.13		Рис.1.14

Аналогичные реакции возникают в шарнирно-скользящей опоре (Рис.1.12) и игольчатой опоре (Рис.1.13).

Заметим, что шарнирно-неподвижную опору (Рис.1.5) можно представить как систему двух шарнирно закреплённых на концах стержней (Рис.1.14).

Пример 1.1

Балка 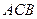имеет шарнирно неподвижную опору в точке и прикреплена к концу троса в точке . Балка нагружена силам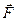и и 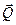, приложенными как показано на Рис. 1.15. Трос переброшен через блок 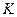и растягивается противовесом 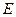. Пренебрегая трением на блоке, определить силу реакции шарнира и силу тяжести противовеса .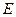

Дано:

Рассмотрим равновесие стержня 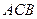. Кроме заданных сил 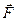и 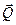, на балку действуют сила реакции троса , приложенная в точке , и сила реакции шарнира, приложенная в точке .

Рис. 1.15		Рис. 1.16

Неизвестную по модулю и направлению силу представим двумя неизвестными по модулю составляющими, направленными вдоль выбранных координатных осей. Направление реакции в точке известно. Заданную силу 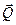имеет смысл разложить в точке 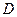на две составляющие, параллельные координатным осям. Силовая схема представлена на Рис.1.16.

Условия равновесия в рассматриваемом случае имеют вид:

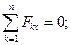
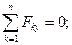
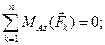
Решая полученную систему уравнений, находим:

Остаётся определить силу тяжести противовеса .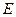

Рассмотрим равновесие тела 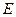(Рис.1.17). Получаем:

Рассмотрим равновесие блока 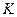(Рис.1.18). Составляя уравнение моментов относительно оси блока, получаем:

Таким образом,

Рис. 1.17		Рис. 1.18

Как видно, натяжения концов нити, переброшенной через блок, при отсутствии трения одинаковые.

Пример 1.2

Ломаный стержень 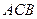имеет шарнирно неподвижную опору в точке и шарнирно подвижную опору в точке . В точке 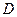приложена сила 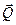, линия действия которой перпендикулярна 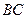(Рис.1.19). Дано: кН, м, м, Определить реакции опор.

Рассмотрим равновесие стержня 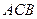. Направление реакции шарнира заранее неизвестно. Можно определить линию действия этой силы при помощи теоремы о трёх силах и решить задачу графически. Однако на таком пути часто возникают хотя и преодолимые, но неоправданные сложности, связанные с решением чисто геометрических проблем. Намного эффективнее аналитический путь решения задачи.

Рис. 1.19		Рис. 1.20

Неизвестную по модулю и направлению силу представим двумя неизвестными по модулю составляющими, направленными вдоль выбранных координатных осей. Направление реакции в точке известно. Заданную силу 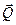имеет смысл разложить в точке 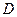на две составляющие, параллельные координатным осям. Силовая схема представлена на Рис.1.20.

Условия равновесия в рассматриваемом случае имеют вид:

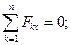
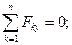
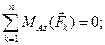
Решая полученную систему уравнений, находим:

Замечание.

Имеет смысл получать решение в общем виде (в буквенных обозначениях). Численные значения следует подставлять только на последнем этапе решения задачи.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Какова методика решения задач об определении реакций опор?
2. Каковы условия равновесия плоской системы сил?
3. Как вычисляется проекция вектора силы на координатную ось?
4. Как вычисляется момент силы относительно оси, перпендикулярной плоскости расположения сил?
5. Как представляется реакция шарнирно-подвижной и шарнирно-неподвижной опор?
6. Как представляется реакция троса, гладкой поверхности и стержневой опоры?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 2.28; 2.29; 2.30; 2.31; 2.41; 4.7; 4.8; 4.10; 4.11; 4.12; 4.13; 4.14; 4.15.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-1.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2