Средняя энергия молекул. Число степеней свободы газовых молекул и теплоемкость газов. Закон равнораспределения энергии по степеням свободы.

Степенями свободыхарактеризуется способность системы (в нашем случае молекулы) совершать независимые движения. В соответствии с видами механического движения различают поступательные, вращательные и колебательные степени свободы.

Числом степеней свободы механической системы называется количество независимых величин, однозначно определяющих ее положение и конфигурацию в пространстве.

Закон равнораспределения по степеням свободы: если система молекул находится в состоянии теплового равновесия при температуре T, то средняя кинетическая энергия равномерно распределена между всеми поступательными и вращательными степенями свободы и для каждой поступательной или вращательной степени она равна kT/2 , а энергия, приходящаяся на колебательную степень свободы, равна kT (где k — постоянная Больцмана).

Средняя полная кинетическая энергия молекулы с жесткими связями, включающая кинетическую энергию поступательного и вращательного движения, вычисляется по формуле .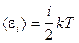

Скорости газовых молекул. Наиболее вероятная, средняя арифметическая и среднеквадратичная скорости газовых молекул.

В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям (v), которое подчиняется закону, теоретически полученному Максвеллом. Закон Максвелла представлен в виде некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) представляет собой отношение доли (относительного количества) молекул dN(v)/N, скорости которых лежат в интервале от v до v + dv, в величине этого интервала dv.

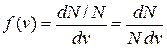(1)

Применяя методы теории вероятности, Максвелл нашел функцию f(v), т.е. закон для распределения молекул идеального газа по скоростям:

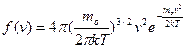(2)

Здесь m_o – масса одной молекулы.

Вид функции этой функции

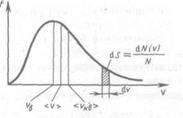
Используя ее можно получить выражения для следующих скоростей молекул:

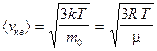— средняя квадратичная;

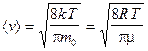— средняя арифметическая;

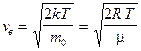— наиболее вероятная,

где т_о— масса одной молекулы.

Барометрическая формула. Распределение Больцмана

Барометрическая формула имеет вид ,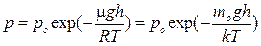

где m — молярная масса газа, R — универсальная газовая постоянная, т_o — масса одной молекулы, k — постоянная Больцмана, Т — термодинамическая температура.

Она показывает, как изменяется атмосферное давление в зависимости от высоты. Из нее, учитывая, что m_ogh = П — потенциальная энергия молекулы в поле тяготения, можно получить

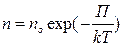
Эта формула называется распределением Больцмана для молекулво внешнем потенциальном поле.