Применение закона Ома и законов Кирхгофа для магнитных цепей.
| Наименование закона | Аналитическое выражение закона | Формулировка закона |
| Первый закон Кирхгофа | 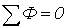 | Алгебраическая сумма магнитных потоков в узле магнитопровода равна нулю |
| Второй закон Кирхгофа | 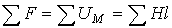 | Алгебраическая сумма падений магнитного напряжения вдоль замкнутого контура равна алгебраической сумме МДС, действующих в контуре |
| Закон Ома | 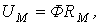 где где 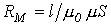 | Падение магнитного напряжения на участке магнитопровода длиной 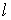 равно произведению магнитного потока и магнитного сопротивления равно произведению магнитного потока и магнитного сопротивления 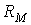 участка участка |
2)Сформулированные законы и понятия магнитных цепей позволяют провести формальную аналогию между основными величинами и законами, соответствующими электрическим и магнитным цепям, которую иллюстрирует табл. 6. Таблица 6.Аналогия величин и законов для электрических и магнитных цепей
| Электрическая цепь | Магнитная цепь |
Ток 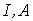 | Поток 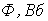 |
ЭДС 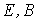 | МДС (НС) 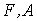 |
Электрическое сопротивление 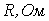 | Магнитное сопротивление 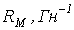 |
Электрическое напряжение 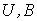 | Магнитное напряжение 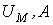 |
Первый закон Кирхгофа: 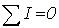 | Первый закон Кирхгофа: 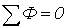 |
Второй закон Кирхгофа: 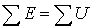 | Второй закон Кирхгофа: 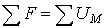 |
Закон Ома: 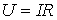 | Закон Ома: 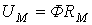 |
3)В неразветвленной магнитной цепи магнитный поток Ф одинаков для различных участков цепи. В ней не содержится магнитных узлов, где сходятся несколько магнитных потоков (более двух) (рис. 33,а). 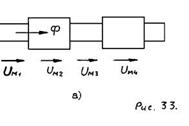 Для последовательной неразветвленной магнитной цепи:
Для последовательной неразветвленной магнитной цепи:
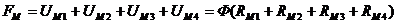
где
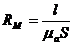
Прямая задача
Задано: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H) (кривая намагничивания) ферромагнитных материалов, из которых выполнена магнитная цепь; 3) магнитный поток Ф, который надо создать в магнитной цепи. Требуется найти намагничивающую силу обмотки F = IW. Решение задачи рассматривается применительно к магнитопроводу, представленному на рис. 4.7.
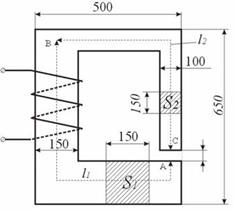
Рис. 4.7. Магнитная цепь
1. Магнитная цепь разбивается на ряд участков с одинаковым поперечным сечением S, выполненном из однородного материала.
2. Намечается путь прохождения средней магнитной линии (на рис. 4.7 показано пунктиром).
3. Т.к. магнитный поток на всех участках цепи остается постоянным, то магнитная индукция B = Ф / S на каждом из участков и напряженность магнитного поля Н неизменны. Это позволяет сравнительно просто определить значение 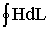 для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку
для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку 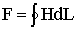 .
.
Запишем интеграл 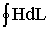 в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда
в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда
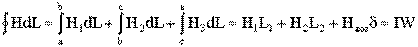 .
.
где: L1 и L2 – длины ферромагнитных участков цепи [м].
δ – ширина воздушного зазора, [м].
4. Значения Н1 и Н2 определяют по известным величинам магнитной индукции В с помощью кривых намагничивания, соответствующих ферромагнитных материалов.
А для воздушного зазора
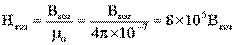 А/м.
А/м.
Обратная задача
Задано:
1. Геометрические размеры магнитной цепи;
2. Характеристики ферромагнитных материалов;
3. Намагничивающая сила обмотки F.
Требуется определить магнитный поток Ф.
Непосредственное использование формулы 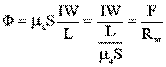 для определния магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи.
для определния магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи.
По полученным данным строят кривую Ф(F) – вебер-амперную характеристику. Имея эту зависимость, нетрудно для заданного значения намагничивающей силы найти величину магнитного потока.
Для оценки необходимого значения Ф можно пренебречь сопротивлением ферромагнитного участка и посчитать поток, который получится под действием намагничивающей силы F при сопротивлении воздушного участка. Это значение Ф заведомо больше расчетного.
Остальные значения можно давать меньше.
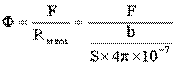 .
.
