Расчет цепи по законам Кирхгофа

Существует большое разнообразие цепей преобразующих ту или иную энергонесущую материю. Какова бы ни была энергонесущая материя (например, электрический ток), и в каком бы режиме ни функционировала преобразующая энергию цепь, существует ограниченный набор универсальных методов для их анализа и расчета. Цель расчета цепей состоит в уточнении величин токов и падений напряжения на элементах во всех режимах работы. Познакомимся с наиболее универсальными методами.

Частичные токи и их возникновения. Методика расчета цепей методом наложения.

Метод эквивалентных сопротивлений и его применение для расчета(?). Как определяется аналитическим способом равнодействующая пространственной системы электрических цепей.

К теме1.3

Контурные токи ЭДС. Расчет цепи методом контурных токов

Метод контурных токов.Решение задач

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m - количество ветвей, а n - количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Основные понятия

Контурный ток - это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС - это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

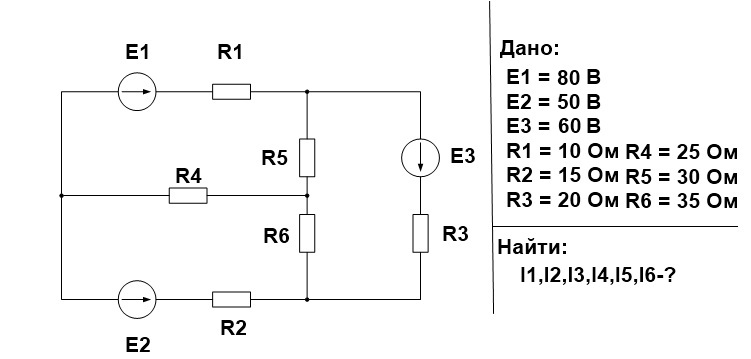
Выполняем все поэтапно.

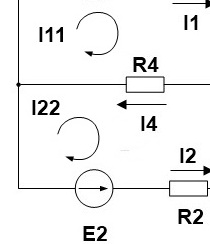
1. Произвольно выбираем направления действительных токов I₁-I₆.

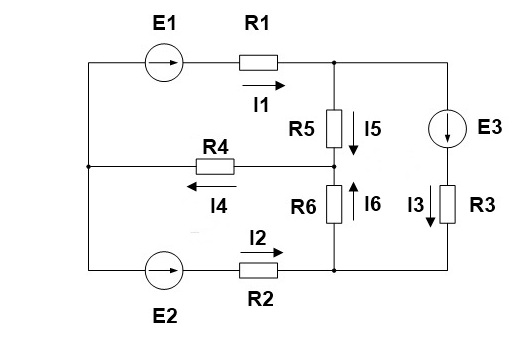
2.Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.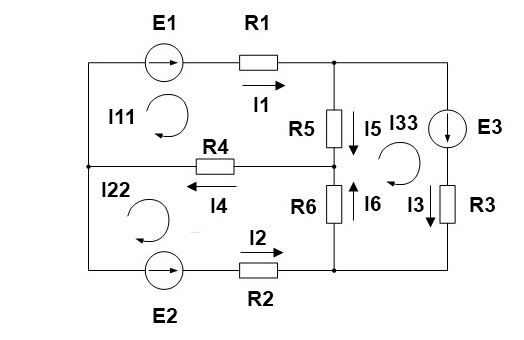

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДСисточников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

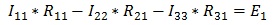
Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

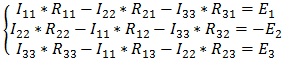
В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

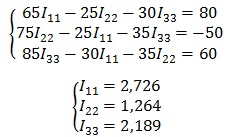
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

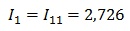
Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

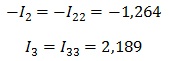
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

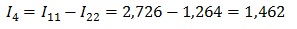
А для остальных

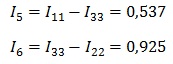
Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!