Порядок расчета погрешностей прямых измерений

Для расчета случайных погрешностей используем некоторые следствия из распределения Стьюдента, которое применяется для малых выборок. Пусть мы имеем выборку из n значений величины х, разных за счет случайных погрешностей, т.е. имеем ряд значений х₁, х₂,.....х_n. Для предварительной оценки необходимо отвергнуть сомнительные результаты (промахи). После этого можно приступить к выполнению расчета погрешности в следующем порядке:

1) определить среднее арифметическое значение выборки по формуле

,

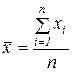где x_i – результат отдельных измерений;

2) рассчитать абсолютное отклонение каждого измерения 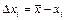и найти их квадраты ;

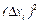3) найти среднее квадратичное отклонение среднего арифметического (для оценки точности конечного числа измерений вместо σ пользуются выборочной средней квадратичной ошибкой среднего арифметического)

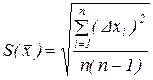
4) задать доверительную вероятность Р (экспериментатор выбирает по своему усмотрению по обыкновению в пределах от 0,9 до 0,99);

5) по таблице 1 определить для заданного числа измерений n и надежности Р коэффициент Стьюдента ;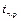

6) вычислить абсолютную случайную погрешность всего эксперимента

;

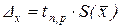7) рассчитать относительную погрешность измерения

;

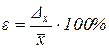8) истинное значение измеряемой величины записать в виде

.

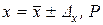Эта запись утверждает, что любое измеренное значение попадает в доверительный интервал от ( 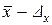) до ( 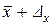) с надежностью Р.

Абсолютная погрешность и результат округляются до одинакового количества знаков после запятой.

4.6. Построение и оформление графиков

При обработке результатов измерений, если необходимо проследить зависимость какой-нибудь физической величины от другой (например, 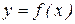) часто пользуются графическим методом. Для этого проводят ряд наблюдений искомой величины у для разных значений переменной величины х. В большинстве случаев пользуются прямоугольной системой координат. По оси абсцисс, как правило, откладывается независимый аргумент х, по оси ординат – функция у. Чаще всего достаточный размер графика 10x16 см. Масштаб выбирают так, чтобы пользоваться графиком было удобно. Масштабы по осям выбирают независимо друг от друга, но так, чтобы график занимал все поле графика. Если точка (0, 0) несет достоверную информацию (например, при построении вольт-амперной характеристики точка U=0, I=0), то она должна быть показана на графике. В большинстве случаев точку (0, 0) на графике показывать необязательно. Единица масштаба должна быть равномерной. В конце оси указываются наименование величины и ее размерность. Множитель, который определяет порядок величины, включается в единицу измерения, например, ”U, мкВ” или ”U, 10^-6B”. Точки на графике необходимо выделять. После нанесения точек проводят наиболее подходящую прямую или кривую так, чтобы точки располагались приблизительно поровну по обе стороны от линии. Если один из результатов резко отличается от всех остальных, его необходимо отбросить, а опыт повторить (если возможно). Не следует соединять точки ломаной линией, поскольку по обыкновению графики физических зависимостей - кривые без резких изломов и перегибов.

На графике могут быть указаны погрешности для одной или двух величин в виде отрезков длиной в доверительный интервал, в центре которых расположены экспериментальные точки. Если необходимо, то по графикам можно найти эмпирическую формулу.

МЕХАНИКА

Лабораторная работа № 101