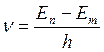Групповая скорость волн де Бройля равна скорости частицы

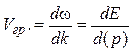
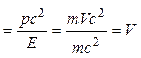
3. Волны де Бройля испытывают дисперсию , то есть их скорость зависит от длины волны.

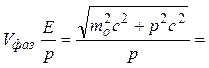
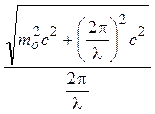
§2. Соотношение неопределённостей Гейзенберга

1. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, p_у, p_z), причем неопределенности этих величин удовлетворяют условиям:

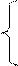
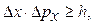
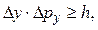
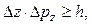
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Другими словами, для микрочастицы невозможно одновременно с большой точностью задать и координату (ее местонахождение) и импульс (ее скорость) так как чем точнее мы определяем координату частицы, т.е. чем меньше Dx , тем более неопределенной становится проекция импульса частицы Dp_x на эту координатную ось и наоборот.

Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта.

2. Влияние массы на соотношение неопределенностей

Учитывая, что p_x = m V_x , можно записать соотношение неопределенностей координаты и проекции скорости на эту координату:

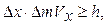
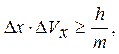
Отсюда следует: чем больше масса частицы, тем меньше неопределенность ее координаты и скорости. То есть, для макрочастицволновые свойства не играют никакой роли: их координаты и скорость могут быть одновременно измерены с достаточно достоверной точностью.

3. Соотношение неопределенностей для энергии Е и времени t :

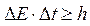
Подчеркнем, что DЕ — неопределенность энергии некоторого состояния системы, Dt — промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни Dt, не может быть охарактеризована определенным значением энергии: разброс энергии DE=h/Dt возрастает с уменьшением среднего времени жизни.

Это означает, что частота излученного фотона также должна иметь неопределенность Dn = DE/h, т. е. линии спектра должны характеризоваться частотой, равной n ± DE/h. Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить времясуществования атома в возбужденном состоянии.

§3 Волновая функция и ее физический смысл

Экспериментальное подтверждение гипотезы де Бройля привели к созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

В квантовой механике состояние микрочастиц описывается с помощью волновой функции Y(x,y,z,t) , которая является основным носителем информации об их корпускулярных и волновых свойствах.

Вероятность нахождения частицы в элементе объемом dV равна dW = |Y|² dV

Квадрат модуля Y (пси) - функции имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z :

|Y|² = dW / dV

Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|² (квадрат модуля амплитуды волн де Бройля), которым задается интенсивность волн де Бройля.

Физический смысл волновой функции:

Волновая функция имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и (х + dx) , у и (у + dy), z и (z+ dz):

Волновая функция Y, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние árñ электрона от ядра вычисляют по формуле

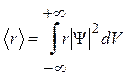
§ 4 Уравнение Шрёдингера

Квантовая механика, описывает законы движения и взаимодействия микрочастиц с учетом их волновых свойств Уравнение Шредингера , играет в атомных процессах такую же фундаментальную роль, как законы Ньютона в классической механике. За создание волновой механики Шрёдингер в 1933 г. удостоен Нобелевской премии.

1. Общее уравнение Шредингера (зависящее от времени)

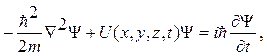
где: 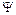(х, у, z,t) — искомая волновая функция частицы.

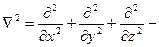оператор Лапласа

U- функция координат и времени, градиент которой, взятый с противоположным знаком, определяет силу, действующую на частицу.

2. Уравнение Шредингера для стационарных состояний:

(если функцияU= U(x, у, z) не зависит явно от времени и имеет смысл потенциальной энергии.

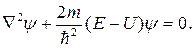
где: Е –общая энергия частицы

3. Уравнение Шредингера для свободной частицы,движущейся в отсутствие силовых полей ( 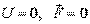) в направлении оси ,

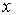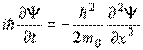
Решением соответствующего уравнения Шредингера является волновая функция

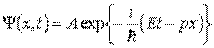
соответствующая плоской волне де Бройля.

Физика атомов и молекул

Модели атома

Первая модель атома Томсона (однородно положительно заряженная сфера, в которую вкраплены электроны) была признана несостоятельной после опытов Резерфорда по рассеянию 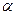-частиц.

Опыт Резерфорда: пучок 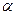-частиц направленный на тонкую золотистую фольгу (Ф) регистрировался после соударения с атомами фольги

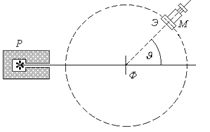Опыты показали, что

Ø некоторые 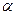-частицы отклонились от первоначального направления,

Ø небольшое количество отразилось от фольги , т. е отклонилось на большие углы (около 180⁰),

Ø а большинство частиц проходило сквозь фольгу, как сквозь пустое пространство.

Выводы Резерфорда: 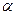-частица может отражаться только от массивного положительного заряда, сосредоточенного в центре атома. Отсюда: планетарная модель атома Резерфорда - весь положительный заряд атома и почти вся его масса сосредоточены в атомном ядре. Вокруг ядра с большой скоростью движутся по круговым орбитам электроны (как планеты вокруг Солнца).

Из модели следует 2 противоречия:

1. Вращаясь, электрон должен испускать свет и терять энергию, т.е. атом должен быть нестабильным (на самом деле атом устойчив);

2. По модели спектр излучения атома должен быть сплошным (на самом деле – атом излучает линейчатый спектр).

Атом водорода в теории Бора

Исходя из идеи Планка о квантовании энергии, Бор на основе модели атома Резерфорда создал свою теорию водородоподобного атома, основанную на трёх постулатах:

Постулаты Бора:

1.Электроны в атоме движутся по стационарным орбитам, среди которых разрешенными являются только те, радиусы которых удовлетворяют условию квантовых значений момента импульса:

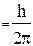
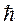
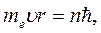(n =1,2,3…)

где - постоянная Планка,

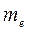- масса электрона,

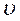- скорость движения электрона по круговой орбите,

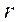- радиус орбиты,

2.Движение электрона по стационарной орбите не сопровождается излучением и поглощением энергии.

3.Испускание и поглощение энергии происходит только при переходе электрона с одной стационарной орбиты на другую.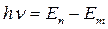

При E_n > E_m – излучение

E_n < E_m - поглощение

Набор возможных дискретных значений частот квантовых переходов определяет линейчатый спектр атомов.