Расчет интерференционной картины от двух источников

(метод Юнга)

Оптическая длина пути L= s n - это произведение геометрической длины s пути световой волны в данной среде на показатель n преломления этой среды, a разность оптических длин проходимых волнами путей D = L₂ – L₁ — называетсяоптической разностью хода.Для воздуха n=1, поэтому оптическая разность хода равна геометрической D=s₂—s₁ .

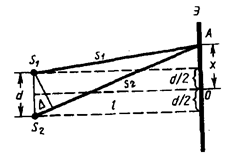Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу. Щели S₁ и S₂ находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей.

Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода D=s₂—s₁. Из рис. имеем

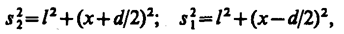
откуда 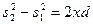, или

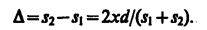
Из условия l >> d следует, что s₁ + s₂ » 2l, поэтому

Условие max →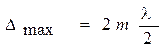

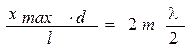
Условие min → .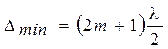

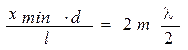Тогда максимумы интенсивности будут наблюдаться в случае, если

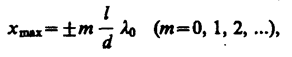
а минимумы — в случае, если

Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы

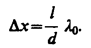
Dx не зависит от порядка интерференции (величины т) и является постоянной для данных l, d и l₀. Согласно формуле, Dx обратно пропорционально d; следовате­льно, при большом расстоянии между источниками, например при d»l, отдельные полосы становятся неразличимыми. Для видимого света l₀»10^–7 м, поэтому четкая, доступная для визуального наблюдения интерференционная картина имеет место при l>>d (это условие и принималось при расчете). По измеренным значениям l, d и Dх, можно экспериментально определить длину волны света.

При освещении монохроматическим светом (l₀=const). интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий т=0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (т= 1), второго (т =2) порядков и т.д.

Если использовать белый свет, то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин воли совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т. д. (ближе к белой полосе будут находиться зоны фиолетового цвета, дальше — зоны красного цвета).

2. Интерференция света в тонких пленках

В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленка на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки.

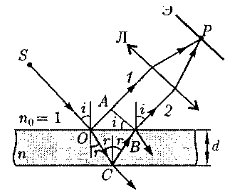Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (п₀=1), а частич­но отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i.

Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В результате возникает интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами.

Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ,

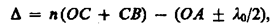
где показатель преломления окружающей пленку среды принят равным 1, а член ± l₀/2 обусловлен потерей полуволны при отражении света от границы раздела. Если п>n₀, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус; если же п<n₀, то потеря полуволны произойдет в точке С и l₀/2 будет иметь знак плюс. Из рис., OC=CB=d/cosr, OA = OB sin i = 2d tg r sin i. Учитывая для данного случая закон преломления sin i = n sin r, получим

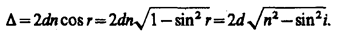
С учетом потери полуволны для оптической разности хода получим

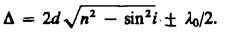
Для случая, изображенного на рис. (п>n₀),

В точке Р будет интерференционный максимум, если

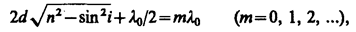
и минимум, если

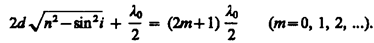
Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называютсяполосами равного наклона.

Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки (рис.), параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, ин­терферирующие лучи 1' и 1" «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. ее оптическая ось параллельна лучам 1' и 1"), в эту же точку придут и другие лучи (на рис. – луч 2), параллельные лучу 1, в результате чего увеличивается общая интенсивность.

Лучи, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы.

Кольца Ньютона

(интерференция на воздушном клине)

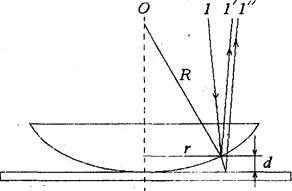Параллельный пучок света (луч 1) падает нормально на плоскую поверхность линзы и частично отражается от верхней (луч 1') и нижней (луч 1'' поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падения света имеющие вид концентрических окружностей.

В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении луча 1'' от стеклянной пластины), и при условии, что показатель преломления воздуха n=1, а i=0,

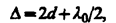
где d—ширина зазора. Из рис. следует, что 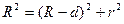, где R—радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d=r²/(2R). Следовательно,

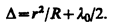
Приравняв Δ к условиям максимума и минимума, получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно

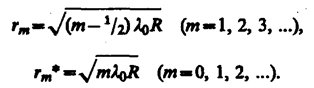
Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы R) определить l₀ и, наоборот, по известной l₀ найти радиус кривизны R линзы.

Кольца Ньютона, являются полосами равной толщины, так как образуются при интерференции от мест равной толщины воздушного клина d .

Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны l₀.

Поэтому при освещении монохроматическим светом (например, красным). наблюдается чередование красных и темных колец.

При освещении белым светом получается совокупность смещенных друг относительно друга радужных колец, образованных лучами разных длин волн.

Все рассуждения были проведены для отраженного света. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на l₀/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.

§4 Дифракция света

Это явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями или огибание волнами препятствий.

Дифракция волн наблюдается, если размеры отверстий или препятствий одного порядка с длиной волны.

Расчет и объяснение дифракции света можно приближенно сделать, используя принцип Гюйгенса-Френеля.

Пусть плоская волна нормально падает на отверстие в непрозрачном экране. Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия

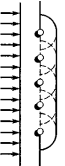Френель дополнил это положение Гюйгенса, введя представление о когерентностивторичных волн и их интерференции. В таком обобщенном виде эти идеи получили название принципа Гюйгенса-Френеля.

Метод зон Френеля

Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l/2, т. е. Р₁М – Р₀М = Р₂М – Р₁М = Р₃М – Р₂М = ... = l/2

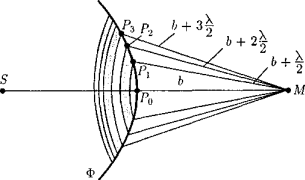
Подобное разбиение фронта волны на зоны можно выполнить, проведя из точки М сферы радиусами b + 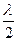, b + 2 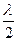, b + 3 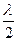, ... . Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

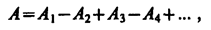
где А₁, А₂, ... — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., т-й зонами.

Если число открытых зон Френеля четное, то на экране в точке наблюдения М будет минимум интенсивности света, в случае нечетного количества зон -максимум.

Различают два вида дифракции:

- дифракции Френеля, или дифракция в расходящихся лучах (наблюдается для сферических волн, если препятствие или отверстие находятся на конечном расстоянии от экрана);

- дифракции Фраунгофера, или дифракция в параллельных лучах (наблюдается для плоских волн, если источник света и точка наблюдения бесконечно удалены от препятствия).

2. Дифракция Фраунгофера на одной щели

Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j,

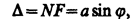
где F — основание перпендикуляра, опущенного из точки М на луч ND.

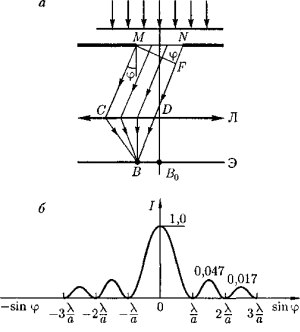Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна l/2

Число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн.

При интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга.

Следовательно, если число зон Френеля четное, то

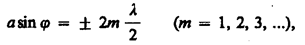
и в точке В наблюдаетсядифракционный минимум(полная темнота), если же число зон Френеля нечетное, то

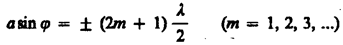
и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.

В точке В₀ наблюдается центральный дифракционный максимум.

Положение дифракционных максимумов зависит от длины волны l, поэтому рассмотренная выше дифракционная картина имеет место лишь для монохроматического света.

При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при j =0 разность хода равна нулю для всех l). Боковые максимумы радужно окрашены, так как условие максимума при любых т различно для разных l. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m=1), второго (т=2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможн.