Индуктивность контура. Явление самоиндукции

.

a) Индуктивность контура

В соответствии с законом Био-Савара-Лапласа индукция магнитного поля пропорциональна величине тока, следовательно и потокосцепление контура пропорционально силе тока

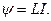
Коэффициент пропорциональности L называют индуктивностью контура. Индуктивность контура зависит от его геометрии и магнитных свойств окружающей среды. Единица индуктивности получила наименование генри: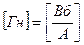

Вычислим индуктивность соленоида бесконечной длины. Индукция магнитного поля внутри такого соленоида

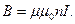
Потокосцепление

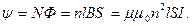
Искомая индуктивность равна

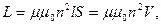
где V- объём соленоида.

b) Явление самоиндукции

Электродвижущая сила индукции возникает при любых изменениях магнитного потока через контур проводника независимо от природы этого потока. В частности, при любом изменении электрического тока в катушке, имеющей N витков, меняется её собственный магнитный поток, пронизывающий плоскости витков, а, следовательно, возникает индукционный ток.

Самоиндукция - это явление возникновения в проводнике электродвижущей силы индукции при изменениях собственного магнитного потока, связанного с изменением тока в этом проводнике.

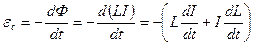
При L = const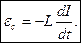

(Если ток I в контуре увеличивается, индукционный ток i направлен навстречу I, если ток в контуре уменьшается, индукционный ток i совпадает с током в контуре I ).

c) Токи при размыкании и замыкании цепи

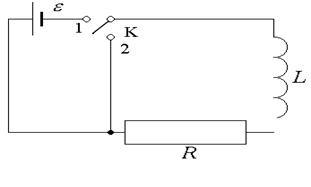Токи самоиндукции в цепи, согласно правилу Ленца, препятствуют изменениям их вызвавшим: стремятся уменьшить нарастающий ток и поддержать убывающий. Это приводит к тому, что установление тока при замыкании цепи, содержащей индуктивность, и его убывание до нуля при размыкании являются процессами, растянутыми во времени.

a) Исследуем процесс размыкания цепи, содержащей индуктивность.

В момент времени t = 0 при силе тока I₀ = e /R отключим цепь от источника питания, переведя переключатель К из положения 1 в положение 2. Уменьшение тока в цепи автоматически порождает э.д.с. самоиндукции, следовательно закон Ома будет записываться линейным однородным дифференциальным уравнением 1-го порядка

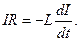
Для решения дифференциального уравнения применим метод разделения переменных

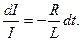
Интегрируя обе части уравнения, получим

→

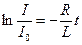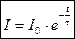
Где 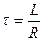время релаксации; 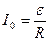сила тока в начальный момент времени.

Следовательно, после отключения источника сила тока в цепи, содержащей индуктивность, убывает по экспоненциальному закону. Скорость убывания определяется временем релаксации t = L /R, т.е. временем, в течение которого сила тока уменьшается в е раз. Чем больше индуктивность цепи, тем больше время релаксации и медленнее уменьшается ток.

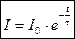
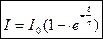
При размыкании цепи При замыкании цепи

Энергия магнитного поля

Для контура индуктивностью L, по которому течет ток I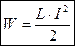

Для соленоида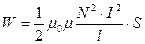

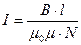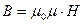Так как и , то: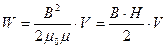

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида V = S∙ l и распределена в нем с объемной плотностью энергии:

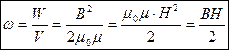
Эффект Холла

(лаб. раб. 305)

Если металл (или полупроводник) с током І поместить в магнитное поле, то в проводнике возникает электрическое поле в направлении, перпендикулярном направлению магнитного поля и направлению тока І.

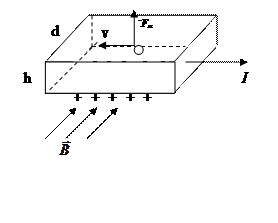Под действием силы Лоренца электроны отклоняются к верхней грани пластины (она заряжается отрицательно), а у нижней грани образуется не скомпенсированный положительный заряд. То есть, между верхним и нижним краем пластины возникает дополнительное поперечное электрическое поле.

h - высота пластины; d - толщина пластины v- скорость движения электронов

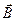Когда напряженность этого поля Е_х достигнет величины, способной уравновесить действие силы Лоренца, установится стационарное распределение зарядов в поперечном (относительно и І ) направлении. Тогда: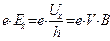

или: 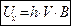( холловская разность потенциалов).

Так как 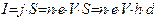, то ,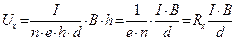

То есть холловская разность потенциалов прямо пропорциональна индукции магнитного поля В, силе тока І и обратно пропорциональна толщине пластины d.

Таким образом, холловская разность потенциалов

,

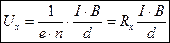где 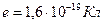- заряд электрона;

n, 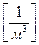- концентрація электронов;

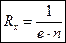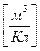, - постоянная Холла.

Постоянная Холла позволяет:

а) определить концентрацию носителей тока в проводнике (если известен характер и заряд носителей);

б) судить о природе проводимости полупроводника, так как знак постоянной Холла совпадает со знаком заряда носителей тока (дырок или электронов).

Эффект Холла используется для изучения энергетического спектра носителей тока в металлах и полупроводниках.

Применяется также для умножения постоянных токов в аналоговых вычислительных машинах , в измерительных приборах (датчики Холла).

Магнитные свойства веществ

(лаб раб. 304)