Влияние течения на путь следования судна.

СНОС

Если в районе плавания действует течение, то перемещение судна относительно земной поверхности будет складываться гео­метрически из элементов движения судна относительно воды и элементов движения самой воды, т. е. течения. Элементами движения судна являются его истинный курс и проходи­мое расстояние, определяемое по соответствующим приборам с уче­том поправок последних. Элементы течения — это его скорость и
направление, обычно выбираемые судоводителями из пособий, со­ставленных на основании многолетних наблюдений.

Пусть судно следует из точки О истинным курсом ИК (рис.75). Отложим из этой точки по линии курса вектор V_n собственной скорости хода судна, учитываемой по лагу (удобнее за 1 ч вре­мени). Из конца этого вектора (точка А) отложим вектор скорости

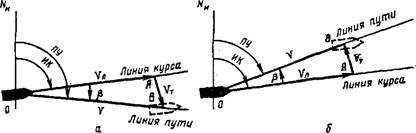Рис. 75. Влияние течения на путь следования судиа: л — при сносе слева; 6 — ери сносе еярава.

течения V_т в том же масштабе. Тогда равнодействующий вектор V (замыкающая ОВ) представит линию пути и истинную скорость хода судна относительно земной поверхности. Направление век­тора V даст путевой угол (ЛУ) судна.

Смещение судна с линии истинного курса, происходящее под влиянием течения, называется сносом от течения или просто сно­сом. Угол Р, на который линия пути отклонена от линии истинного курса под влиянием течения, называется углом сноса от течения или поправкой на течение.

Численно путевой угол, истинный курс и угол сноса связаны алгебраически соотношением

ПУ = ИК + Р-

Если течение пересекает линию истинного курса судна слева (см. рис. 75, а), то угол 0 имеет положительное значение, если справа (см. рис. 75, б) — то отрицательное.

Треугольник ABC, образованный векторами V_a, V_T и V, назы­вается навигационным треугольником.

Подобное построение делают на карте, когда по заданному истинному курсу и элементам течения требуется определить пу­тевой угол судна. Если масштаб карты мал, то берут двухчасовые скорости хода судна и течения.

Пример. Судно со скоростью хода 12 у?лов следует ИК = 290°. Те~ чение по румбу StO со скоростью 2,6 узла. Найти ПУ судна, угол сноса Q) к истинную скорость хода судна (V).

Решение. Произведем графическое построение (рис. 76) и получим ПУ = = 278°,0; Р = 12°,0, V = 10,8 узла.

На практике чаще приходится решать обратную задачу: по известным элементам течения и движения судна определять ис­тинный курс судна для следования по заданному пути.

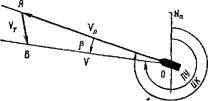Пусть судно при наличии течения должно следовать из точки О по линии пути ПУ (рис. 77). Отложим из исходной точки вектор V_T часовой скорости течения. Из конца этого вектора (точка В)

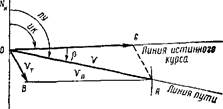Рис. 76. Графическое построение оп- Рис. 77. Определение истинного ределения путевого угла, угла сноса курса с учетом течения, и истинной скорости хода судна.

радиусом, равным вектору ]/_л часовой скорости хода судна, сде­лаем засечку на линии заданного пути (точка А). Тогда линия OA, проведенная от исходной точки до места засечки (точка Л) представит вектор V истинной скорости хода судна.

Линия ОС, параллельная вектору V„, про­веденная из исходной точки, представит со- Ы_и бой линию истинного курса судна; угол меж­ду истинным меридианом и этой линией даст истинный курс ИК., а угол между ней и ли­нией пути — угол сноса р.

Пример. Судно должно следовать по пути 174°,0; имеется течение направлением 230,0 скоро­стью 2,5 узла; скорость хода судна по лагу Vn 10 узлов. Определить истинный курс судна, истинную скорость и угол сноса.

Решение. Сделав построение (рис. 78), получа­ем: V = 11,2 узла, И К = 161°,5 и Р = —12° ,0.

Ведя на карте прокладку с учетом тече­ния, строят навигационный треугольник и продолжают вести как линию пути, так и линию курса (рис. 79). Над линией пути над­писывают значение компасного курса, поп­равки компаса и угла сноса с его знаком, например ГКК 111^о,0' (—0,5) =— 9°,0'.

Рис. 78. Графическое построение определения истин­ного курса, истинной скорости и угла сноса судна.

Расстояние, пройденное по лагу с учетом его поправки (лаг течения не учитывает), откладывают по линии истинного курса, а. не по линии пути. Проведя из полученной точки на данный момент (точка А на рис. 79) линию по направлению течения, на пересече­нии ее с линией пути (точка В) получают счислимое место. При отсутствии лага пройденное рас­стояние, рассчитанное по истин­ной скорости хода судна, взятой из навигационного треугольни­ка, откладывают по линии пути непосредственно.

Траверз какого-либо пункта относят, как и при дрейфе, к линии истинного курса и в точке пересечения линии траверза с линией пути (рис. 79), получа­ют место судна на момент прохождения траверза предмета.

Предвычисление отсчета лага и момента времени в заданной точке при плавании на течении осуществляют следующим образом: при исходной точке строят навигационный треугольник; из заданной точки на линии пути проводят встречно направле­нию течения прямую до пересечения ее с линией истинного курсам снимают с карты по линии истинного курса расстояние 5 от

исходной точки до полученной точки пересечения и рассчитыва-

g

ют РОЛ по формуле рол = —:

^Л л

рассчитывают отсчет лага в заданной точке: ОЛ₂ =РОЛ-\-ОЛ₁, где ОЛ\ — отечет лага в исходной точке; рассчитывают время t

S .

перехода до заданной точки t_s — — » находят момент времени

Ул

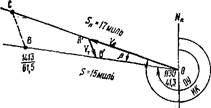Рис. 80. Графическое построение оп­ределения ПУ, р, V, а также 0Л2 иНа­

Т₂ прихода в заданную точку Т₂ = Тi X t_s, где Т_{ — момент времени при нахождении судна в исходной точке.

пример. Судно, имея вис­ходной точке О на момент 7** = 11ч 30 мин, ОЛ^ = 41,3, следует ИК 290° с собственной скоростью хода 9 узлов. Течение по румбу SSO; К_т=2 узла. Кл = 0,85. Определить ПУ, р, V, а также ОЛ_ъ и Т₂ в точке В, находящейся в расстоянии 15 миль.

Решение. 1) Построим навигаци­онный треугольник (рис. 80) и по­лучим ПУ = 280°,0; Р = —10°,0; V = 9 узлов.

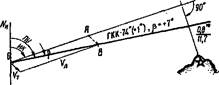Рис. 79. Прокладка пути судна на. карте при сносе.

2) Откладываем по линии пути расстояние S = 15 миль и получаем точку В. Из нее проводим встречно течению (т. е. на NNW) прямую и получаем на пересечении ее с лини­ей курса точку С.
Сняв расстояние ОС, находим, что S = 17 милям, и рассчитываем

РОЛ = ---------- — = 20 миль.

0,85

3) Определяем ОЛ.₂ = 41,3 -f 20,0 =» 61,3 мили.

5) Рассчитаем продолжительность перехода t= —jj—=1,88 ч = <=1ч 53 мин.

6) Получим Т₂ = 11 ч 30 мин -f» 01 ч 53 мин == 14 ч 13 мин.

Отсчет лага и момента времени прихода на траверз какого- либо предмета рассчитывают следующим образом. Строят нави­гационный треугольник, проводят из точки местонахождения предмета прямую в направлении ИК — 90° к линии истинного кур­са. На пересечении этой прямой с линией пути получают счисли- мое место судна на момент прохождения траверза предмета. По расстоянию от исходной точки до точки пересечения траверза с линией курса рассчитывают ОЛ₂ и Т₂ на момент прохождения траверза предмета.

Аналитически учесть влияние течения на путь следования суд- , на можно исходя из того, что векторы скоростей, являясь сторо­нами навигационного треугольника, связаны определенными со­отношениями. На практике такие вычисления заменяют выбор­ками из специальных таблиц (табл. 32, а, 32, б и 32 МТ — 75).

Точность счисления при плавании на течении играет важную роль. Следует учитывать, что данные об элементах течений, при­водимые в пособиях и на картах, являются более или менее при­ближенными и в той или иной степени отличаются от действитель­ных. Поэтому при плавании в районах течений к счислению надо относиться с осторожностью. Более надежным является счисление при плавании на постоянном устойчивом течении, например пассат­ном. Плавая, на течении, следует возможно чаще определять место судна всеми доступными в данных условиях способами.