Разность широт и разность долгот

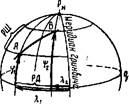■Рис. 18. Разность широт и разность долгот.

В навигации приходится рассчитывать разность в положении по широте и по долготе каких-либо двух пунктов, например пунк­тов прихода и отхода судна.

Рис. 19. Зависимость разности широт и разно­сти долгот от курса судна.

Разностью широт (РШ) называют кратчайшую дугу меридиа­на между параллелями двух пунктов — Л и В (рис. 18). Широту пункта отхода обозначают через ср_ь а широту пункта прихода —
®₂. Разности широт придают наименование «к N» или «к5» в зави­симости от того, севернее или южнее лежит пункт прихода относи­тельно пункта отхода судна. Например, у судна, переходящего из точки А в точку В (см. рис. 18), РШ к S. Наименование разности широт не зависит от того, в одном и том же или в разных полу­шариях лежат пункты отхода и прихода, а зависит только от их взаиморасположения и истинного курса судна.

Разностью долгот (РД) называется меньшая дуга экватора между меридианами пунктов отхода и прихода, долготы которых обозначают соответственно через ^ и (см. рис. 18). Разность долгот имеет наименование «к 0^si» или «к Wt> в зависимости от того, восточнее или западнее расположен пункт прихода судна относительно пункта отхода. Так, если судно следует из точки А к точке В, то РД к 0^s1, а при обратном следовании РД к W.

Наименование разности долгот не зависит от полушарий, в ко­торых расположены пункты отхода и прихода, а подобно разности широт определяется только взаиморас­положением пунктов и истинным кур­сом судна.

Судно, следуя каким-либо курсом,в первой четверти истинного горизонта ИЬ(i (рис. 19) совершает (делает) РШ к N и РД к О'; во второй четверти го­ризонта ИКг — РШ к S и РД к 0^st; в третьей четверти горизонта ИКз — РШ к 5 и РД к W и в четвертой четверти И К4 — РШ kN и РД к W.

Разности широт и разности долгот выражаются формулами:

РШ = ъ-п, РД = Х₂-Х_х.

Эти формулы алгебраические, при­чем северные широты и восточные дол­готы условно считают положительными величинами, а южные широты и запад­ные долготы — отрицательными и при­дают им соответствующие знаки «плюс» (+) или «минус» (—). Кроме того, раз­ности широт к N и разности долгот к Qst считают положительными, а разнос­ти широт к S и разности долгот к W - придавая им соответствующие знаки.

Случаи разности широт и разности долгот, когда пункт отхода и пункт прихода лежат в одном и том же полушарии, показаны на рис. 20.

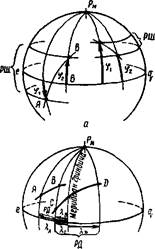Рис. 20. Зависимость от по­лушарий: широт; 6 — разности

а — разности долгот.

отрицательными, также

Если оба пункта лежат в одном и том же полушарии, то РШ
может заключаться в пределах 90", а если в разных — то в пре­делах 180°.

При расчете разности долгот, если пункты лежат в разных полушариях, может получиться, что РД как алгебраическая раз­ность Яг и окажется и более 180°. Например, если A,i = 122°, 0'O^st, а Л2= 145°Й7, то РД=2ЬТ к W. В подобных случаях по­лученную величину надо вычесть из 360° и применить наименова­ние РД на обратное. В данном случае имеем РД=360°—267°=93° к O^st.

При расчетах РШ и РД возможны случаи, когда число минут вычитаемого окажется больше, чем уменьшаемого. Тогда из числа градусов уменьшаемого занимают 1°, т. е. 60 мин, и прибавляют их к числу минут уменьшаемого. Например, если из 60°15' требу­ется вычесть 39°40', получим 60°15'—39°40'=59°75'—39°40' = —20°35'.

При суммировании величин может оказаться, что число минут в сумме превысит 60 или будет равно 60. Тогда надо 60 мин вы­честь из суммы и, приняв их за 1°, прибавить к числу градусов. Например, сумму величин 65°25' и 10°40' выражают 62°25'+ + 10^о40'=72^о65'=73°05'.

Расчеты производят по схеме, приведенной в следующих при­мерах.

Пример. Рассчитать РШ для пунктов: a) qpj = 19°45' N; ср_а = 27°08' N; б) ф! = 72°33'S; <р₂ = 60°09'S; в) ф_х = 30°40'N; ф₂ = 14°48'S.

Решение, а) ср₂ = —27°08' б) <р₂ = —60°09' в) <?₂ = —14°48' = — 26=68' — у_г = — 72°33' — _У1 = — 30°40'

— — 19°45' pjjj _ j _Г24, рщ _ — ₄₄о₈₈,

РШ = + 7°23' = 12°24' к N = — 45 28'

= 7°23 к N = 45^с>29' к S

Пример. Рассчитать РД для пунктов: а) А., = 38°21'O^s' = 20°47' O^s/; б) Xi = 15°15'№; к₂ = 37°53'O^s/; в) Х_х = 160°30'Г; Х₂ = 120°40'0^S'.

Решение, а) Х₂ = — 20°47' б) Х₂ = + 37°53'

— \₁₌₌ _ 38°2Г = — 37°8Г — X_t = — 15⁰15'

РД = — 17°34' РД = — 52°68'

= 17°34' к W = 53°08' к О

в) X, = + 120°40' 360=00' = 359°60'

— X_t = — 160°30' 28Г10'

РД — + 281°10' _st рд = —78°50'

= 281° 10' к О = 78°50' к W,

К приведенным примерам делают графические построения.