Электродинамические и электромагнитные воздействия

§6. - ДЕЙСТВИЕ ЗАМКНУТОГО ТОКА НА ЭЛЕМЕНТ НЕЙТРАЛЬНОГО ТОКА*

Пусть будут величинами положительных и отрицательных зарядов двух элементов в двух проводниках, один расположенный в т. (x',y',z'), другой в т. (x,y,z). В соответствии с гипотезой, полные заряды являются предельно малыми в сравнении с , … Сила, действующая со стороны ds'на ds, равна сумме воздействий и иа и . Скорости движения проводников и связанных с ними положительных ионов - V, V'. Скорости отрицательных ионов - v, v '. Относительные скорости V-v=η, V'-v'= η'. И, наконец, токи J, J' имеют направления ds(dx, dy, dz)и ds'(dx ', dy ', dz '). В итоге мы будем иметь

Подставим эти значения в выражение (13) для Fx, и раскроем знак суммы. Множитель 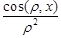будет коэффициентом в выражении

.

Это и есть электростатическое воздействие.

Элементы будут множителем перед ds ds' и

Отсутствующие здесь члены были сокращены посредством цикличной перестановки x y z. Выражение может быть записано в виде

Если результирующие заряды E, E ' оказываются нулевыми, то остаётся только последний член. В остальных же случаях оказываются крайне малыми. И поскольку всё ещё должно домножаться на 1/c², то легко видеть, что первый член окажется абсолютно незначащ в сравнении с электростатическим членом. Второй член соответствует очень слабому воздействию нейтрального тока на движущийся электрический заряд, третий - воздействию этого заряда на ток или магнит (эффект Роуланда). Эти два эффекта имеют одинаковый порядок величины и проявляются только в очень тонких экспериментах, или когда V или V ' велики. Если электростатический член мал, как это обычно и бывает, то они абсолютно незначащи. Мы обсудим эффект Роуланда позже.

Квадратичные члены также крайне малы в сравнении с , так что остаётся только этот последний член:

Аналогично, члены и ощутимый вклад дают лишь в форме результата пропорционального JJ '. И мы будем иметь для набора членов, зависящих от скоростей,

Согласно формуле Лоренца (20), воздействие ds' на ds , на основании аналогичного рассуждения, даётся выражением

члены E, E ' и квадратичные члены снова оказываются незначительными. Что же касается члена, содержащего ускорения, который одинаков в обеих теориях, то он опять же домножается на или , и потому оказывается незначащ, если ускорения не слишком велики, что не имеет места в условиях эксперимента, где наблюдаются электродинамические или электромагнитные действия.

Я утверждаю, что результат воздействия замкнутого контура ds' на элемент ds одинаково следует из (25) и из (26). Фактически,

поскольку

Член dx ds' cos(ρ,ds') имеет, следовательно, полный дифференциал, зависящий от s'. Его интеграл для замкнутого контура равен нулю. Аналогично

и интегрирование по частям вдоль s' преобразует этот член в

так что это даёт для искомого результирующего воздействия, испытываемого элементом ds,

Именно это и дало бы интегрирование выражения (26). Константа k исчезает из результата. Кроме того, последний результат не зависит от движения проводников и их деформации, при условии, что J и J ' остаются постоянными, и что элемент тока Jds является нейтральным, а ток J ' – замкнутым и нейтральным. Вращательные действия токов и магнитов объясняются здесь классически.

Для k = -1 сила взаимодействия двух элементов нейтрального тока в точности давалась бы формулой Ампера. В таком виде эта формула может быть признана даже сегодня.

Когда вопрос ставится о теле двух или трёх измерений, пересечённом нейтральным током, распределённым вдоль замкнутых линий, то результирующие воздействия на другие элементы объёма находятся в соответствии с формулой. Но, помимо этого, токи слегка изменят своё направление, как мы увидим в следующем разделе: это - проявление эффекта Холла. Но эффект этот минимален, и его здесь можно не учитывать.

Эффекты же магнетизма, как это принято, получаются путём замены магнитов молекулярными замкнутыми нейтральными токами. Здесь, опять же, нет разницы между теориями.