Ферромагнетизм. Кривая намагничивания. Магнитный гистерезис. Точка Кюри. Домены. Спиновая природа ферромагнетизма.

J=cH; [J]=A/м²=[H]

J-намагниченностьJ=∑P_m /∆V, P_m=ISn-магнитный момент

Н-вектор напряженности `H=B/m₀-J

-спиновый магнитный момент(в отсутствии эл поля- хаотически ориентированы, что суммарный магнитный момент=0.

Под действием поля - установка в одном направлении)

Силы которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу что приводит к возникновению областей спонтанного намагничивания называются обменными силами.

c-магнитная восприимчивость. c=m-1, m-отн магнитная проницаемость

В зависимости от c вещества подразделяются на:

-диамагнетики(c<0, c@10^-5-10^-6)

-парамагнетики (c>0, c@10^-3-10^-4)

-ферромагнетики (c>0, c@10³-10⁴ а так же c(Н) !)

Ферромагнетики – особый класс веществ(сильных магнетиков), обладающих большим намагничиванием даже в отсутствии поля.

( Fe, Ni , Co и другие)

Домены – малые макроскопические области самопроизвольно намагниченые до насыщения.

за магнитные свойства вещества ответственны собственные магнитные моменты электрона .

В слабых полях происходит смещение границ доменов -'поедание' доменами , направленных в направлении поля других.В сильных полях-поворот в направлении поля Н

Для каждого ферромагнетика существует определённая температура ( точка Кюри ) при которой он теряет свои магнитные свойства. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме.

Магнитный гистерезис-отставание изменения величины намагниченности(J) ферромагнетика от изменения внешнего магнитного поля вследствие c(Н)вследствие сил 'внутреннего трения' между доменами.

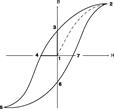
Рис. 2. ТИПИЧНАЯ ПЕТЛЯ ГИСТЕРЕЗИСА для магнитно-твердого ферромагнитного материала. В точке 2 достигается магнитное насыщение. Отрезок 1–3 определяет остаточную магнитную индукцию, а отрезок 1–4 – коэрцитивную силу, характеризующую способность образца противостоять размагничиванию.

Она характеризуетнеоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1– 3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.

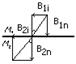
20. Граничные условия для векторов магнитной индукции и напряженности магнитного поля (вывод).

`В- вектор магнитной индукции [Тл=F_m/IÙl], F_m-максимальная сила,действующая на участок проводника с током

`H- вектор напряженности магнитного поля [А/м]

В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н: B=m₀`Hгде m₀ –магнитная постоянная, имеющая универсальное значение 4p 10^–7 Гн/м

Линии `Вв вакууме создаются макротоками и замкнуты.

∳В_ndS=0;

∳ℍ_ldl=∑I_макр

след:

В1n=B2n

m₁m₀H_1n=m₂m₀H_2n =>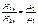

Для тангенсальных компанент:

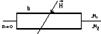
∳ℍ_ldl=H_1ib+H_ia-H_2ib+H_ia=∑I_макр=0

H_2i=H_1i

H= ; =>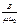

-------------------------------------------------------------------------------------------------

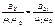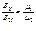
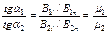
21. Электромагнитная индукция. Закон Фарадея-Максвелла и его вывод из закона сохранения энергии. Метод измерения индукции Столетова.

Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 году. Он опытным путём установил, что при изменении магнитного поля внутри замкнутого контура в нём возникает электрический ток, который называют индукционным током. (Опыты Фарадея можно

воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.

Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием магнитный поток.

Магнитным потоком через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции В на площадь контура S и на косинус угла a между на-

правлением вектора магнитной индукции и нормалью к площади контура. Ф=BScosa

Опытным путём был установлен основной закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по величине скорости изменения магнитного потока через контур.ЭДС индукции= -dФ/dt.

[ Ф ]= вебер (Вб): 1 Вб=В/с.

Из основного закона -dФ/dt.следует смысл размерности: 1 вебер – это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нём ЭДС индукции 1 В.

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 году опытным путём установил русский учёный Ленц.

Правило Ленца: