Связь между потенциалом и напряженностью электрического поля.
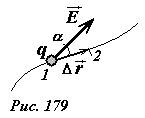
Потенциал является важной характеристикой электрического поля, он определяет всевозможные энергетические характеристики процессов, проходящих в электрическом поле. Кроме того, расчет потенциала поля проще расчета напряженности, хотя бы потому, что является скалярной (а не векторной) величиной. Безусловно, что потенциал и напряженность поля связаны меду собой, сейчас мы установим эту связь. Пусть в произвольном электростатическом поле точечный заряд q совершил малое перемещение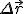 
из точки 1 в точку 2 (Рис. 179). Пренебрегая изменением напряженности поля 
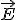на этом участке, работу, совершенную полем можно записать в виде
.
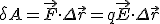По определению эта величина равна разности потенциалов, взятой с противоположным знаком, деленной на величину заряда, поэтому
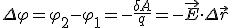. (1)
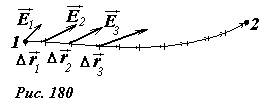
Если расстояние между точками 1 и 2 не является малым, то необходимо эти точки соединить произвольной линией (Рис. 180), разбить ее на малые участки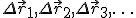 
и просуммировать разности потенциалов между (1) ними
. (2)
Формула (2) позволяет рассчитать разность потенциалов между произвольными точками, по известным значениям напряженности поля во всех точках.
Б 40
Эквипотенциальные поверхности. Вычисление потенциала в поле заданных зарядов (точечный заряд, система точечных зарядов, непрерывно распределенный заряд).
Эквипотенциальная поверхность — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю или к ньютоновскому гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.
Поверхность проводника в электростатике является эквипотенциальной поверхностью. Кроме того, помещение проводника на эквипотенциальную поверхность не вызывает изменения конфигурации электростатического поля. Этот факт используется в методе изображений, который позволяет рассчитывать электростатическое поле для сложных конфигураций.
В (стационарном) гравитационном поле уровень неподвижной жидкости устанавливается по эквипотенциальной поверхности. В частности, приближенно можно утверждать, что по эквипотенциальной поверхности гравитационного поля Земли проходит уровень океанов[1]. Форма поверхности океанов[2], продолженная на поверхность Земли, называется геоидом и играет важную роль в геодезии. Геоид, таким образом является эквипотенциальной поверхностью силы тяжести, состоящей из гравитационной и центробежной составляющей.
Пусть имеется один точечный заряд q. Это частный случай сферической симметрии. У нас есть формула:
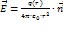, где q(r) – заряд внутри сферы радиуса r, но если заряд точки, то для точечного заряда q(r)=q , при любом r. Понятно почему, на любом радиусе внутри сферы точка остаётся точкой. И для точечного заряда
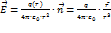. Это поле точечного заряда. Потенциал поля точечного заряда: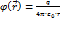 
Пусть мы имеем систему зарядов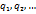 
, тогда напряжённость поля, создаваемая системой точечных зарядов, в любой точке равна сумме напряжённостей, создаваемых каждым из зарядов. Я мог бы сразу написать 
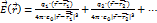, если бы вы свободно читали формулы. Учитесь читать формулы повествовательно. Заряд 
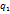умножьте на вектор 
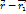, и разделите на модуль этого вектора, а что такое модуль вектора это длина. Эта вся штука даёт вектор, направленный вдоль вектора .
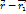Процедура вычисления потенциала эл.поля, созданного распределенным зарядом.
Если эл.поле задается зарядом, распределенным по объему и непрерывным в пространстве,то потенциал такого электрост. поля вычисляется следующим образом:
dφ = dq / 4πε0|R-r|
φ = ∫ dq / 4πε0|R-r| R-r
Б 41