Распределение скоростей молекул по Максвеллу. Наивероятнейшая скорость.
Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)3/2 V2 exp(MV2/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, градусы Кельвина, К;
М - молярная масса, кг/моль, численно равная молекулярной массе;
R = 8,3144 Дж/(моль•К) - универсальная газовая постоянная в системе СИ
Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нем обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.
Б 23
Явление переноса.
В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса. В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движения (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным. В противном случае это нестационарный процесс. Стационарные процессы возможны только в стационарных внешних условиях. В термодинамически изолированной системе могут возникать только нестационарные явления переноса, направленные на установление равновесного состояния
Б 24
Предмет и метод термодинамики. Основные понятия. Первый закон термодинамики.
Принцип построения термодинамики довольно прост. В ее основу положены три экспериментальных закона и уравнение состояния: первый закон (первое начало термодинамики) — закон сохранения и превращения энергии; второй закон (второе начало термодинамики) указывает направление, по которому протекают естественные явления в природе; третий закон (третье начало термодинамики) утверждает, что абсолютный нуль температуры недостижимТермодинамика, в отличие от статистической физики, не рассматривает конкретные молекулярные картины. На основании опытных данных формулируются основные законы (принципы или начала). Эти законы и их следствия применяются к конкретным физическим явлениям, связанным с превращением энергии макроскопическим путем (без учета атомно-молекулярного строения), изучают свойства тел конкретных размеров. Термодинамический метод используется в физике, химии, ряде технических наук.
Термодинамика – учение о связи и взаимопревращениях различных видов энергии, теплоты и работы.
Понятие термодинамики произошло от греческих слов «термос» – теплота, жар; «динамикос» – сила, силовой.
Под телом в термодинамике понимают некоторую часть пространства, заполненную веществом. Форма тела, его цвет и другие свойства для термодинамики несущественны, следовательно, термодинамическое понятие тела отличается от геометрического.
Важную роль в термодинамике играет внутренняя энергия U.
U – сумма всех видов энергии, заключённых в изолированной системе (энергия теплового движения всех микрочастиц системы, энергия взаимодействия частиц, энергия электрических оболочек атомов и ионов, внутриядерная энергия и т.д.).
Внутренняя энергия является однозначной функцией состояния системы: её изменения DU при переходе системы из состояния 1 в 2 не зависит от вида процесса и равно ∆U = U1 – U2. Если система совершает круговой процесс, то:
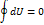
Полное изменение её внутренней энергии равно 0.
Внутренняя энергия U системы определяется её состоянием, т. е. U системы есть функция параметров состояния:
U = f(p,V,T) (1)
При не слишком высоких температурах, внутреннюю энергию идеального газа можно считать равной сумме молекулярно-кинетических энергий теплового движения его молекул. Внутренняя энергия гомогенной, а в первом приближении и гетерогенной систем является аддитивной величиной – равной сумме внутренних энергий всех её макроскопических частей (или фаз системы).
Б 25
