Поверхностное натяжение и лапласово давление. Капиллярный эффект, когезия и адгезия.
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными
Лапласово давление- это давление под искревлённой поверхностью жидкости. представьте поверхность воды, из которой виднеется стеклянная трубка- она капилляр. величина и знак лапласового давления находятся по формулам, потому что при поднятии и при отпускании жидкости через капилляр, давление жидкости должно быть одиниково для всех уровней данного капилляра
Капилля́рность (от лат. capillaris — волосяной), капиллярный эффект — физическое явление, заключающееся в способности жидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах. Поднятие жидкости происходит в случаях смачивания каналов жидкостями, например воды в стеклянных трубках, песке, грунте и т. п. Понижение жидкости происходит в трубках и каналах, не смачиваемых жидкостью, например ртуть в стеклянной трубке.
Благодаря капиллярности возможны жизнедеятельность животных и растений, различные химические процессы, бытовые явления (например, подъём керосина по фитилю в керосиновой лампе, вытирание рук полотенцем). Капиллярность почвы определяется скоростью, с которой вода поднимается в почве и зависит от размера промежутков между почвенными частицами.
Капиллярами называются тонкие трубки, а также самые тонкие сосуды в организме человека и других животных (см. Капилляр (биология)).
Области применения
Капиллярный эффект используется в неразрушающем контроле (капиллярный контроль или контроль проникающими веществами) для выявления дефектов, имеющих выход на поверхность контролируемого изделия. Позволяет выявлять трещины с раскрытием от 1 мкм, которые не видны невооруженным глазом.
Когезия (от лат. cohaesus — связанный, сцепленный), сцепление молекул (ионов) физического тела под действием сил притяжения. Это силы межмолекулярного взаимодействия, водородной связи и (или) иной химической связи. Они определяют совокупность физических и физико-химических свойств вещества: агрегатное состояние, летучесть, растворимость, механические свойства и т. д. Интенсивность межмолекулярного и межатомного взаимодействия (а, следовательно, силы когезии) резко убывает с расстоянием. Наиболее сильна когезия в твердых телах и жидкостях, то есть в конденсированных фазах, где расстояние между молекулами (ионами) малы — порядка нескольких размеров молекул. В газах средние расстояния между молекулами велики по сравнению с их размерами, и поэтому когезия в них незначительна. Мерой интенсивности межмолекулярного взаимодействия служит плотность энергии когезии. Она эквивалентна работе удаления взаимно притягивающихся молекул на бесконечно большое расстояние друг от друга, что практически соответствует испарению или сублимации вещества
Адгезия (от лат. adhaesio — прилипание) в физике — сцепление поверхностей разнородных твёрдых и/или жидких тел. Адгезия обусловлена межмолекулярным взаимодействием (вандерваальсовым, полярным, иногда — образованием химических связей или взаимной диффузией) в поверхностном слое и характеризуется удельной работой, необходимой для разделения поверхностей. В некоторых случаях адгезия может оказаться сильнее, чем когезия, то есть сцепление внутри однородного материала, в таких случаях при приложении разрывающего усилия происходит когезионный разрыв, то есть разрыв в объёме менее прочного из соприкасающихся материалов.
Б 16
Понятие потока жидкости (газа) и уравнение непрерывности. Вывод уравнения Бернулли.
В гидравлике потоком считают такое движение массы, когда эта масса ограничена:
1) твердыми поверхностями;
2) поверхностями, которые разделяют разные жидкости;
3) свободными поверхностями.
В зависимости от того, какого рода поверхностями или их сочетаниями ограничена движущаяся жидкость, различают следующие виды потоков:
1) безнапорные, когда поток ограничен сочетанием твердой и свободной поверхностей, например, река, канал, труба с неполным сечением;
2) напорные, например, труба с полным сечением;
3) гидравлические струи, которые ограничены жидкой (как мы увидим позже, такие струйки называют затопленными) или газовой средой.
Живое сечение и гидравлический радиус потока. Уравнение неразрывности в гидравлической форме
Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ωx, ωy,ωz угловой скорости w.
Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:
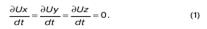
Если теперь сложить
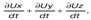
то получим
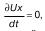
Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:
dx = Uxdt; dy = Uy dt; dz = Uzdt. (3)
Теперь помножим каждое уравнение (3) соответственно на dx, dy, dz, и сложим их:
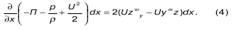
Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:

Нами получено уравнение Бернулли
Анализ уравнения Бернулли

это уравнение есть не что иное, как уравнение линии тока при установившемся движении.
Отсюда следуют выводы:
1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.
2) пропорциональны строки 1 и 2, т. е.

Уравнение (2) является уравнением вихревой линии. Выводы из (2) аналогичны выводам из (1), только линии тока заменяют вихревые линии. Одним словом, в этом случае условие (2) выполняется для вихревых линий;
3) пропорциональны соответствующие члены строк 2 и 3, т. е.

где а – некоторая постоянная величина; если подставить (3) в (2), то получим уравнение линий тока (1), поскольку из (3) следует:
ωx= aUx; ωy= aUy; ωz= aUz. (4)
Здесь следует интересный вывод о том, что векторы линейной скорости и угловой скорости сонаправлены, то есть параллельны.
В более широком понимании надо представить себе следующее: так как рассматриваемое движение установившееся, то получается, что частицы жидкости движутся по спирали и их траектории по спирали образуют линии тока. Следовательно, линии тока и траектории частиц – одно и то же. Движение такого рода называют винтовым.
4) вторая строка определителя (точнее, члены второй строки) равна нулю, т. е.
ωx= ωy= ωz= 0. (5)
Но отсутствие угловой скорости равносильно отсутствию вихревости движения.
5) пусть строка 3 равна нулю, т. е.
Ux = Uy = Uz = 0.
Но это, как нам уже известно, условие равновесия жидкости.
Анализ уравнения Бернулли завершен.
Б 17
