Определение коэффициента теплопроводности твердого тела

Выполнил студент ________________, группа___________, дата____________.

Допуск ______________

Выполнение __________

Зачет ________________

Цель работы: Ознакомиться с явлением теплопроводности и определить опытным путем коэффициент теплопроводности.

Приборы и материалы

№ п\п	Наименование прибора	Цена деления	Предел измерения (хmax)	Точность отсчета (Δхпр)
	Прибор для определения коэффициента теплопроводности твердых тел	-	-	-
	Калориметр	-	-	-
	Термометр
	Мензурка
	Часы

Теоретические сведения

Основные понятия и законы

Явления переноса

Явления переноса – кинетические, необратимые процессы, в результате которых в физической системе происходит пространственный перенос электрического заряда, массы, импульса, энергии, энтропии или какой-либо др. физической величины.

Причины явлений переноса — действие внешнего электрического поля, наличие пространственных неоднородностей состава, температуры или средней скорости движения частиц системы. Перенос физической величины происходит в направлении, обратном градиенту[12] этой величины.

Явления переноса приближают систему к состоянию равновесия.

К явлениям переноса относятся: электропроводность — перенос электрического заряда под действием внешнего электрического поля; диффузия — перенос вещества (компонента смеси) при наличии в системе градиента его концентрации; теплопроводность — перенос теплоты вследствие градиента температуры; вязкое течение — перенос импульса, связанный с градиентом средней массовой скорости.

Приведённые примеры относятся к явлениям переноса в гомогенных[13] системах, внутри которых отсутствуют поверхности раздела.

Явления переноса происходят также в гетерогенных[14] системах, состоящих из гомогенных частей (подсистем), отделённых друг от друга или естественными поверхностями раздела (как жидкость и её пар), или полупроницаемыми мембранами.

При появлении в гетерогенной системе разности (перепада) электрического потенциала, давления, температуры между подсистемами возникают необратимые потоки заряда, массы и теплоты. К подобным явлениям относятся: электрокинетические явления — перенос заряда и массы из-за перепада электрического потенциала и давления: термомеханические эффекты — перенос теплоты и массы из-за перепада температуры и давления. Явления переноса в газах изучает кинетическая теория газов.

Теплопроводность в твердых телах

Теплопроводность относится к явлениям переноса, причиной её является наличие градиента температуры между частями тела.

Теплопроводность – это передача внутренней энергии от одной части тела к другой без переноса вещества.

Молекулярно-кинетическая теория вещества объясняет этот процесс следующим образом. Так как температура – это мера средней кинетической энергии молекул, то различие температур двух участков тела свидетельствует о том, что кинетические энергии молекул в этих участках различны. Поэтому молекулы двух соприкасающихся слоев, сталкиваясь, передают свою кинетическую энергию от слоя к слою.

Уравнение теплопроводности

Количественно явление теплопроводности во всех телах описывается уравнением Фурье, согласно которому количество тепла dQ, прошедшее за время dt через некоторую площадку S, перпендикулярную направлению распространения тепла, выражается формулой:

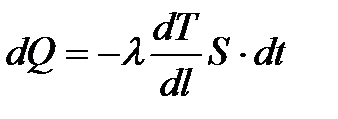
Как следует из формулы, l измеряется в СИ в единицах Дж/(м×с×К).
Величина dT / dl характеризует быстроту изменения температуры в направлении распространения тепла и численно равна изменению температуры тела на единице длины в этом направлении. Она называется градиентом температуры. Знак минус в уравнении Фурье указывает, что поток тепла направлен в сторону, противоположную градиенту температуры.

Коэффициент l, зависящий от физической природы вещества и его состояния, называется коэффициентом теплопроводности. Физический смысл его можно установить из следующих соображений. Если положить в формуле (4) S = 1; dt = 1; и dT / dl = 1, то dQ = l. Это означает, что коэффициент теплопроводности численно равен количеству тепла, переносимому за 1 секунду через единицу площади, перпендикулярной направлению распространения тепла, если градиент температуры равен единице.

Можно доказать, что l= (1/3) с_V ρ <ν> <l>,

где с_V — удельная теплоемкость газа при постоянном объеме (количество теплоты, которое необходимо для нагревания 1 кг газа на 1 К при постоянном объеме), ρ — плотность газа, <ν> — средняя скорость теплового движения молекул, <l> — средняя длина свободного пробега.

Теория лабораторной работы

Теоретические сведения

В настоящей работе рассматривается теплопроводность металлов. Если взять металлический стержень и нагревать один конец его, то начнется перенос энергии и температура различных его участков будет повышаться. Дойдя до известного предела, температура для каждого определенного участка стержня делается постоянной. Такое состояние потока тепловой энергии, при котором температура отдельных участков тела с течением времени не меняется, является установившимся, или стационарным. При этом количество энергии, получаемой данным участком, равно количеству энергии, которое он отдает соседним.

В основу работы положен закон теплопроводности Фурье, который в интегральной форме имеет следующий вид:

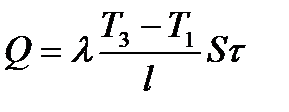(1)

где S – площадь сечения стержня, м²; l – длина стержня, м; Т₂ – температура горячего слоя, ^оС; Т₁ – температура холодного слоя, ^оС; t – время в течение которого происходит перенос энергии, с.

Коэффициент пропорциональности l и является коэффициентом теплопроводности данного вещества. Величина 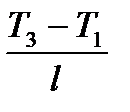представляет собой изменение температуры на единицу длины в направлении передачи теплоты и называется градиентом температуры.

Из формулы (1): 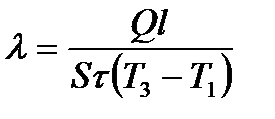, Вт/(м×К).

сеть

E

D

B

F

T

A

F

O

Рис. 1

L

Описание установки

Для определения коэффициента теплопроводности l служит прибор, схематически представленный на рис.1, где O – кипятильник;
D – электрический нагреватель; Е – калориметр; L – металлический стержень, l которого требуется определить в настоящей работе (его длина l и поперечное сечение S указаны на стенде около прибора); FA и FB – металлические пластинки для увеличения контакта стержня с водой в кипятильнике и калориметре.

Доведя воду в кипятильнике при помощи электрического нагревателя D до кипения и добившись стационарного потока через стержень L, с помощью термометра Т измеряют в течение времени t повышение температуры воды в калориметре Е от некоторого начального значения Т₁ до конечного Т₂ (так как температура конца стержня, находящегося в калориметре, во время опыта повышается, то стационарность теплового потока, о которой здесь идет речь, лишь приблизительна).

За время t в калориметр (допустим, что отсутствуют потери в окружающий воздух) поступит некоторое количество тепла Q. Это количество тепла, с одной стороны, можно выразить формулой (1), с другой стороны, если отсутствуют потери тепла, то все количество тепла Q пойдет на нагревание калориметра, пластинки F и воды. Поэтому, обозначив через m и c – массу и удельную теплоемкость калориметра; через m₁и c₁ – массу и удельную теплоемкость пластинки FB, находящейся в калориметре Е; и через c_в и M – массу и удельную теплоемкость воды в калориметре, Q можно записать:

Q = (mc + m₁c₁ + c_в M)×(Т₂ – Т₁).

Величину(mc + m₁c₁ + c_в M), Дж/К, представляющую суммарную теплоемкость системы, обозначим через С_S. Тогда

Q = С_S (Т₂ – Т₁). (2)

Применяя формулу (1) для рассматриваемого количества тепла, нужно иметь в виду, что температура конца стержня, находящегося в калориметре, за время наблюдения изменяется от Т₁ до Т₂. Поэтому за температуру конца стержня, находящегося в калориметре, принимают среднюю его температуру:

.

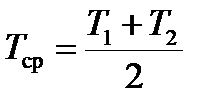В формуле (1) температура Т₃ = 100⁰С - температура кипящей воды в кипятильнике. С учетом указанных замечаний формула (1) примет вид:

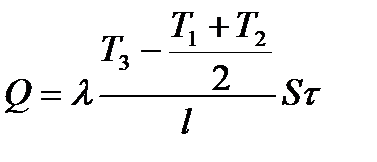. (3)

Приравнивая значения Q из (2) и (3), получим

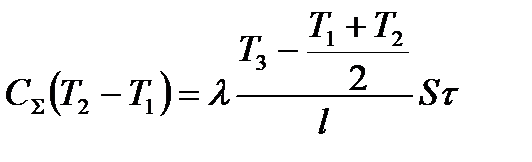, откуда

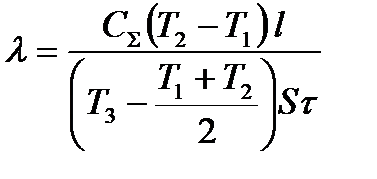.(4)