Определение модуля сдвига вращающегося твердого тела при помощи крутильного маятника

Выполнил студент ________________, группа ____________, дата __________.

Допуск ______________

Выполнение __________

Зачет ________________

Цель работы: ознакомиться с деформациями сдвига, кручения и методами определения модуля сдвига на основе деформации кручения.

Приборы и материалы

№ п\п	Наименование прибора	Цена деления	Предел измерения (хmax)	Точность отсчета (Δхпр)
	Маятник крутильный с грузами	-	-	-
	Секундомер
	Линейка

Теоретические сведения

Основные понятия и законы

Деформация

Деформация (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.

Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия (другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (т.е. выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.

Наиболее простые виды деформации тела в целом: растяжение-сжатие, сдвиг, изгиб, кручение.

В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.

Деформация твёрдого тела может явиться следствием фазовых превращений, связанных с изменением объёма, теплового расширения, намагничивания (магнитострикция), появления электрического заряда (пьезоэлектрический эффект) или же результатом действия внешних сил.

Механическое напряжение

Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.

Механическое напряжение σ равно отношению модуля силы упругости F_упр к площади поперечного сечения тела S:

,

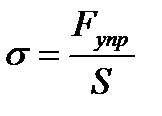Измеряется механическое напряжение в Па: .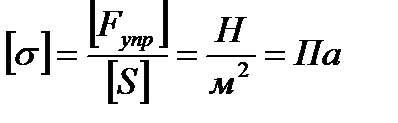

Символом σ обозначают, как правило, нормальное напряжение, когда деформирующая сила перпендикулярна (нормальна) к поверхности образца.

Если деформирующая сила действует на образец по касательной, то говорят о касательном напряжении τ.

Закон Гука

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид

F_упр = – k Dl (1)

где F_упр – модуль силы упругости, возникающей в теле при деформации;
Δl = l – l₀ – абсолютное удлинение тела, l₀ – первоначальная длина.
Величина e = Δl / l₀ называется относительным удлинением тела.

Коэффициент k называется жесткостью тела– коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.

Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.

В СИ жесткость измеряется в ньютонах на метр (Н/м):

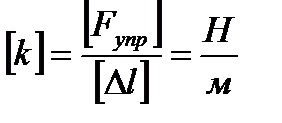
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.

Закон Гука для одностороннего растяжения (сжатия) формулируют так:

сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению e:

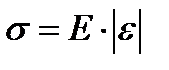(2)

Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.

Коэффициент пропорциональности Ев законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что модуль Юнгачисленно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.

Докажем это:

из закона Гука получаем, что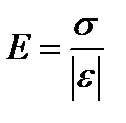

Если модуль Юнга E численно равенмеханическому напряжению σ, то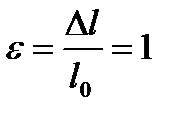

Тогда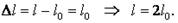

Измеряется модуль Юнга в Па: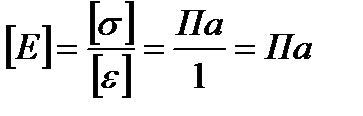

Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l₀, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.

Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2) 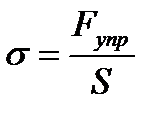и 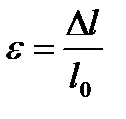, получим:

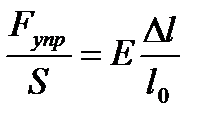или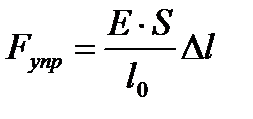

где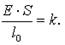

Диаграмма растяжения

Используя формулу

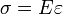
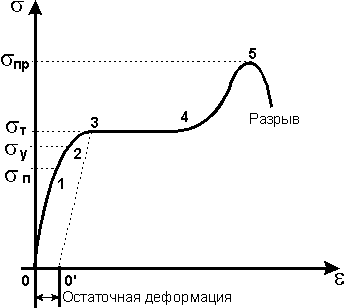по экспериментальным значениям относительного удлинения можно вычислить соответствующие им значения нормального напряжения , возникающего в деформированном теле, и построить график зависимости s от e.

Этот график называют диаграммой растяжения.

На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения s_п, при котором еще выполняется закон Гука, называют пределом пропорциональности.

При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение s_у нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной.

Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение s_т, при котором остаточная деформация достигает заданного значения, называют пределом текучести.

При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4-5 графика). Максимальное значение нормального напряжения s_пр, при превышении которого происходит разрыв образца, называют пределом прочности.

Кручение

Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

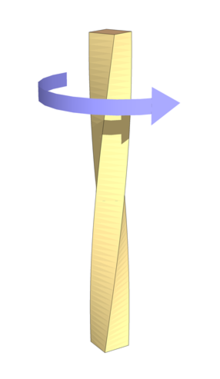
Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

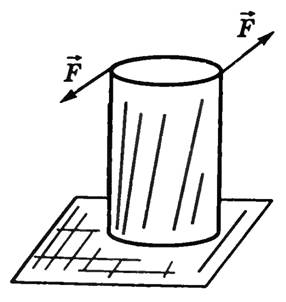
Рис. 1.

Отношение угла закручивания φ к длине 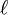называют относительным углом закручивания

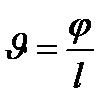
Закон Гука для малых деформаций кручениявыражается формулой

M = G_кр.j

где G_кр.– модуль кручения.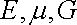

Модуль кручения 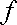, помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения G_кр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

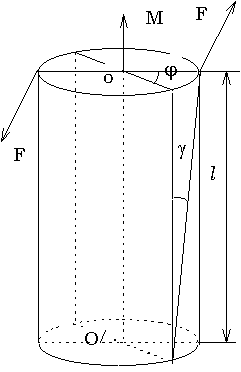
Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

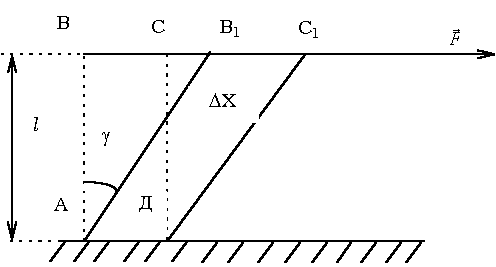
Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

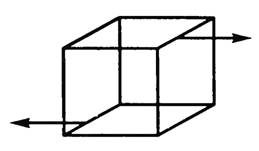
Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

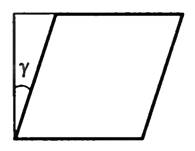
Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде:

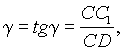
где СС₁ = D X - абсолютный сдвиг, 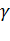- угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг 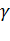пропорционален касательному напряжению 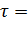F_τ/S, где S - площадь поверхности грани ВС, т.е.

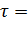F_τ / S = Gg

где G - модуль сдвига, F_τ – касательная сила.

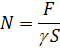
Закон Гука для малой деформации сдвига выражается формулой:

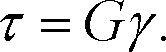
Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра.

Теория лабораторной работы

Теоретические сведения

f

f

L

O /

O

Рис. 6

Пусть к одному концу проволоки или стержня, закрепленного с другого конца, приложена пара сил ff с моментом M (рис. 6). Под действием этой пары сил проволока будет закручиваться. Отдельные поперечные сечения проволоки, перпендикулярные ее оси, будут поворачиваться относительно соседних сечений на некоторые углы. Нижнее сечение повернется относительно верхнего на угол j, который называется углом кручения.

Тогда по закону Гука, справедливому для малых деформаций, момент пары сил M будет прямо пропорционален углу кручения:

М = G_кр j,

где G_кр – модуль кручения.

Между модулем кручения G_кр и модулем сдвига материала проволоки G имеется простое соотношение:

,

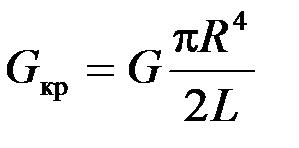где L – длина проволоки; R – радиус проволоки; G – модуль сдвига материала проволоки.

Если твердое тело, подвешенное на проволоке, закрутить на малый угол j и предоставить самому себе, то оно будет вращаться вокруг оси, совпадающей с осью проволоки. При вращении твердое тело будет совершать колебания вокруг первоначального положения равновесия. Такие колебания вращающегося тела являются крутильными колебаниями, а твердое тело – крутильным маятником.

Второй закон Ньютона для вращательного движения в случае крутильного маятника запишется в виде: M = – Ie.

Здесь M – вращающий момент относительно оси проволоки; I – момент инерции тела относительно той же оси; 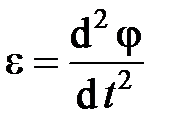– угловое ускорение.

Знак «минус» возник вследствие того, что направление вращающего момента M противоположно направлению углового ускорения e.

Таким образом, .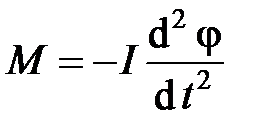

При кручении M = G_крj, поэтому .

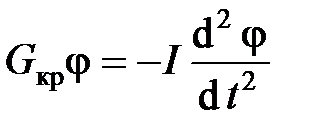Отсюда для крутильного маятника угловое ускорение:

,

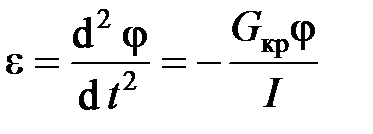т.е. оно прямо пропорционально угловому смещению j и направлено противоположно ему.

Если ускорение тела прямо пропорционально смещению (линейному или угловому) и направлено противоположно ему, то колебания тела являются гармоническими. Коэффициент пропорциональности между ускорением и смещением есть квадрат круговой частоты колебаний. Таким образом, при малых углах кручения крутильный маятник совершает гармоническое колебательное движение.

Угловая частота этих колебаний определяется из уравнения

,

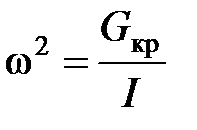а период полного колебания крутильного маятника 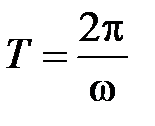определяется выражением

.

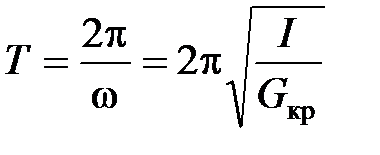Для периода простого колебания 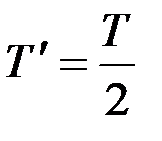имеем:

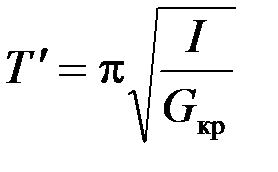. (3)

Описание установки

Прибор для определения модуля сдвига состоит из кронштейна, укрепленного на стене, в котором зажата проволока ОО^/ из испытуемого материала. К нижнему концу проволоки прикреплен горизонтальный стержень рр^/ с резьбой (рис. 7), на который навинчиваются грузы (цилиндры) массами m и m₁. Эти грузы навинчиваются в двух положениях: aa₁ и bb₁. Массы грузов одинаковы: m = m₁. Если такую систему закрутить на малый угол и предоставить самой себе, то ее можно рассматривать как крутильный маятник, период простого колебания которого определяется выражением (3).

b1

b

а

а1

l2

l2

l1

l1

o

Р

Р/

o/

Рис. 7

В данной работе определяются два периода колебаний маятника, соответствующие двум положениям грузов на стержне (рис. 7).

Пусть I₁ – момент инерции системы, когда грузы находились в положении aa₁, I₂ – момент инерции системы, когда грузы находились в положении bb₁, I₀ – момент инерции стержня относительно оси ОО^/.

Тогда: 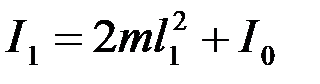, 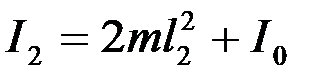. (4)

Период простого колебания маятника, соответствующий положению грузов aa₁:

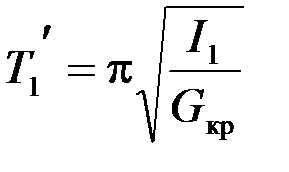, (5)

Период простого колебания, соответствующий положению грузов bb₁:

.

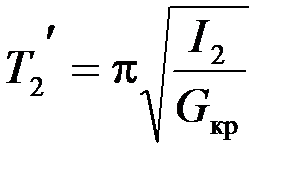Из уравнений (4) и (5) находим: ,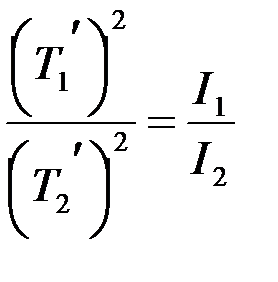

Откуда: 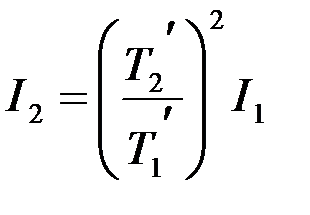. (6)

Из уравнений (17) исключаем l₀:

.

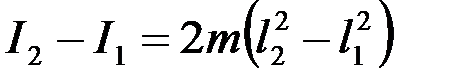Подставив сюда выражение для I₂, из выражения (6) найдем

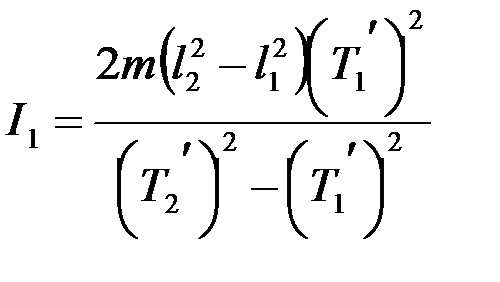
Модуль кручения G_кр находим из формулы (5), подставив в нее выражение для I₁:

.

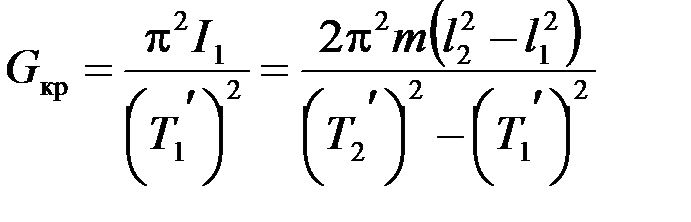Зная модуль кручения G_кр, легко найти модуль сдвига материала проволоки:

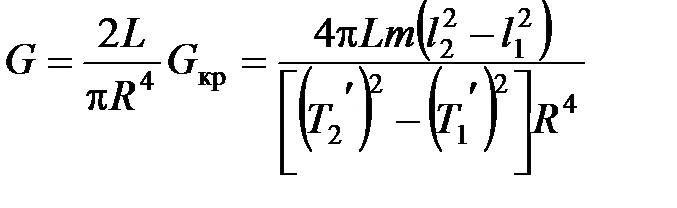. (7)