Порядок операций при обработке результатов серии измерений

При прямых измерениях:

1. Результаты каждого измерения записать в таблицу.

2. Вычислить среднее значение из n измерений

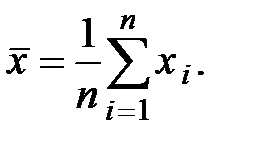
3. Найти погрешности отдельных измерений

.

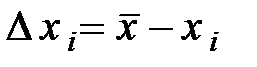4. Вычислить квадраты погрешностей отдельных измерений

(D x₁)², (D x₂)²,..., (D x_n)².

5. Оценить среднеквадратичную погрешность среднего значения

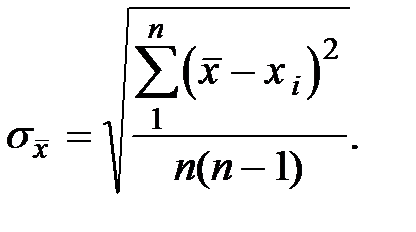
6. Определить коэффициент Стьюдента t_na (по таблице) для доверительной вероятности Р = 0,95 и числа произведенных измерений n.

7. Найти случайную погрешность результата измерений:

.

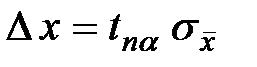8. Если случайная погрешность результата измерений Dx окажется сравнимой* с систематической (погрешностью прибора Dx_пр), то в качестве погрешности результата измерений следует взять величину

.

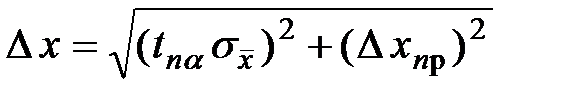9. Окончательный результат записать в виде:

.

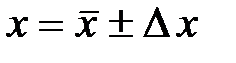10. Оценить относительную погрешность результата измерений

.

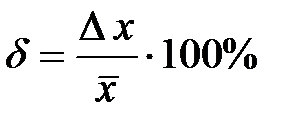При косвенных измерениях:

1. Для каждой непосредственно измеренной величины (X₁, X₂,..., X_m), входящей в расчетную формулу для определения X (X = f (X₁, X₂,..., X_m)), провести обработку в описанной выше последовательности, т.е. вычислить средние арифметические значения 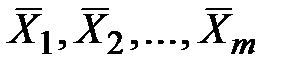по формуле (1) и случайные погрешности D X₁, D X₂,..., DX_m по формуле (4) для доверительной вероятности Р = 0,95.

2. При необходимости учесть систематическую (приборную) погрешность каждой серии измерений

,

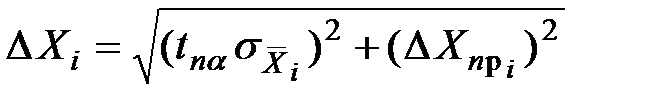где индекс i относится к соответствующей измеренной величине, а DX_{пр i} – систематическая погрешность прибора, используемого для измерения Х_i.

3. Вычислить наиболее вероятное значение X:

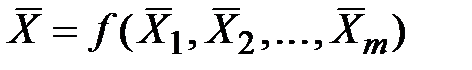
4. Вычислить частные производные 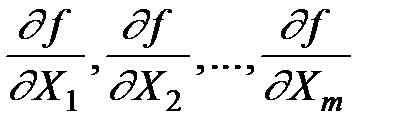при средних значениях величин X₁, X_2,..., X_m.

5. Определить абсолютную погрешность косвенного измерения X по общей формуле:

.

Здесь и выше m – число независимых непосредственно измеренных величин.

6. Записать окончательный результат в виде

.

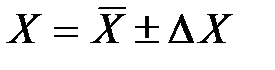7. Определить относительную погрешность косвенного измерения X :

.

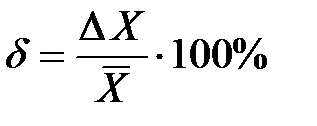Правила представления результата измерения

Все результаты измерений, а также вычисленный по ним окончательный результат приводят вместе с погрешностью, которую выражают в тех же единицах, что и саму измеряемую величину, например: l = (1,572 ± 0,004) м.

Среднее значение <x> необходимо округлять так, чтобы оно оканчивалось цифрой того же разряда, что и Δх после её округления. Т.е. число и его погрешность всегда записывается так, чтобы их последние цифры принадлежали одному и тому же десятичному разряду. Значения погрешностей следует округлять, оставляя одну значащую цифру[2]. Округлять предпочтительно в сторону большего значения.

Примеры:

1. Получено: U = 124,4 В; ΔU = 1,1 В.

Следует записать: U = (124,0 ± 1,0) В.

2. Получено: V = 2,678•10³ см/с; ΔV = 1,2 см/с.

Следует записать: V = (2,678 ± 0,001)•10³ cм/с.

В промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащие цифры.

При представлении окончательных результатов физических измерений часто применяют запись числовых значений в виде десятичной дроби, умноженной на необходимую степень числа десять.

Примеры:

1. При обработке группы результатов измерений получены:
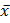= 965,332 и Δх = 8,35.

Результат округления записывают в виде: х = 965 ± 8.

2. При обработке группы результатов измерений получены:
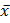= 0,003893 и Δх = 0,000282.

Результат округления записывают в виде: х = (38,9 ± 2,8)•10⁴.

3. Числа 3106; 0,0285; 0,120 записывают так:

3,106•10³; 2,85•10^-2; 1,2•10^-1.

Графическое представление результатов измерений

В большинстве лабораторных работ требуется представить результаты в виде различного рода графиков. Их правильное построение требует соблюдения несложных правил.

1. Масштабы и начала отсчета по координатным осям выбираются так, чтобы график изображения зависимости занимал большую часть поля чертежа. При этом на пересечении осей не обязательно должны находиться нулевые значения величин.

Правильно Неправильно

2. При выборе масштаба необходимо помнить, что точность построения графика должна быть не ниже точности измерений.

3. На осях координат откладываются равноотстоящие друг от друга деления масштаба так, чтобы было удобно работать с графиком. Значения, полученные в эксперименте, не указываются.

Неправильно

Неудачно

Правильно

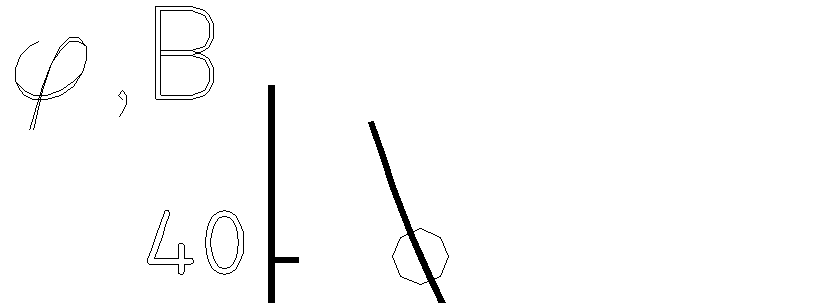
4. В конце координатных осей обязательно указываются условные обозначения откладываемых величин и, через запятую, их единицы измерения.

5. Экспериментальные значения величин (точки) отчетливо наносятся вместе с погрешностями - отрезками длиной в доверительный интервал, расположенными параллельно соответствующей оси, в виде: ┼ , │ , ─ , ˥ .

Если при построении кривой в выбранном масштабе доверительные интервалы не видны вдоль обеих осей координат, экспериментальные точки проставляются в виде маленьких кружочков (треугольников и т.д.) с центром в точке, соответствующей экспериментальным данным.

6. Экспериментальная кривая проводится плавно через доверительные интервалы всех или большинства экспериментальных точек так, чтобы экспериментальные точки наиболее близко и равномерно располагались с разных сторон кривой.

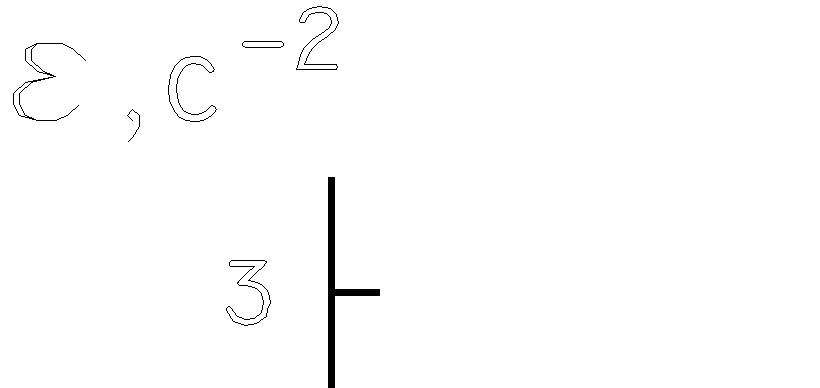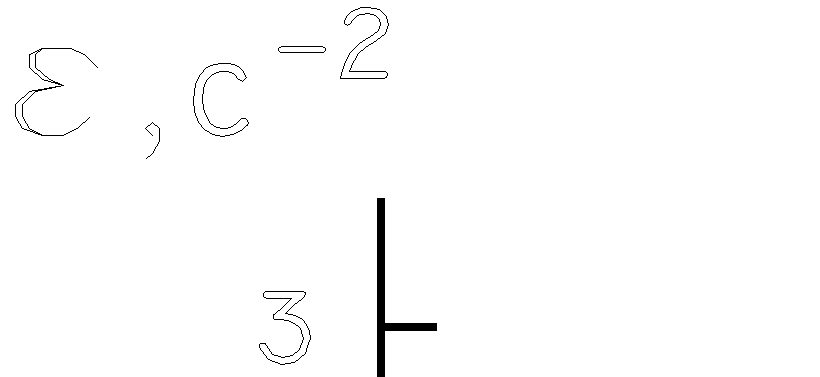Правильно Неправильно

7. Если на графике изображается теоретическая кривая, то указывается формула, по которой она рассчитывается.

8. При изображении нескольких кривых на одном поле графика каждая из них нумеруется или выделяется каким-то другим способом. В свободной части поля даются соответствующие пояснения.

9. График должен содержать надпись, из которой было бы ясно физическое содержание представленной закономерности.

Лабораторная работа 3