Как пользоваться штангенциркулем

Перед началом измерений штангенциркулем надо осмотреть его и проверить на точность. Для этого надо совместить губки инструмента. При этом нулевые риски обеих шкал должны совпасть. Одновременно должен совместиться десятый штрих нониуса с девятнадцатым штрихом миллиметровой шкалы.

Держат штангенциркуль в правой руке так, чтобы четыре пальца руки обхватывали штангу, а большой палец ложился на рифленый выступ подвижной рамки. Подвижную рамку перемещают большим пальцем. Штангенциркуль нужно держать перпендикулярно измеряемой поверхности, чтобы губки всей поверхностью касались измеряемой поверхности. Если держать штангенциркуль под углом, то он будет касаться измеряемой поверхности противоположными углами губок, что внесет погрешность в считываемый размер.

При измерении наружных размеров деталь зажимают между нижними губками, при измерении внутренних размеров верхние губки раздвигают до упора в стенки отверстия, глубину отверстий измеряют с помощью штыря-глубиномера (рис.3). Используя верхние заострённые губки как ножки обычного циркуля, можно штангенциркулем проводить круги на металлических, деревянных, пластмассовых и иных поверхностях.

Результаты всех трёх измерений в целых миллиметрах определяют по положению нулевого деления на линейке плюс доли миллиметров, замеренные по нониусу.

При внутренних измерениях к показаниям штангенциркуля по основной и нониусной шкалам прибавляется толщина губок, которая указана на них. Пример измерения диаметра отверстия представлен на рис.4:

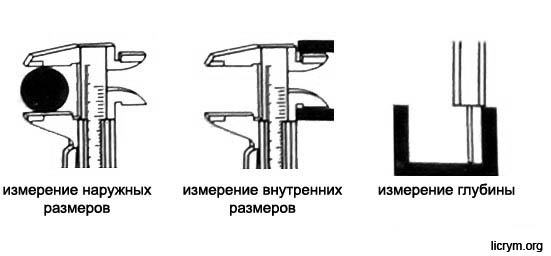
Рис.3.

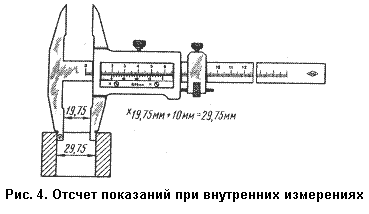
Рис. 4. Отсчет показаний при внутренних измерениях

Порядок отсчёта показаний штангенциркуля по шкалам штанги и нониуса:

· считают число целых миллиметров, для этого находят на шкале штанги штрих, ближайший слева к нулевому штриху нониуса, и запоминают его числовое значение;

· считают доли миллиметра, для этого на шкале нониуса находят штрих, ближайший к нулевому делению и совпадающий со штрихом шкалы штанги, и умножают его порядковый номер на цену деления (0,1 мм) нониуса;

· подсчитывают полную величину показания штангенциркуля, для этого складывают число целых миллиметров и долей миллиметра;

· при измерении штангенциркулем целое число миллиметров отсчитывают по миллиметровой шкале до нулевого штриха нониуса, а десятые доли миллиметра — по шкале нониуса начиная от нулевой отметки до той риски, которая совпадает с какой-либо риской миллиметровой шкалы (рис. 5).

На рис. 5 показаны положения шкал штангенциркуля при отсчёте размеров:

а – 0,5 мм; б – 6,9 мм; в – 34,3 мм.

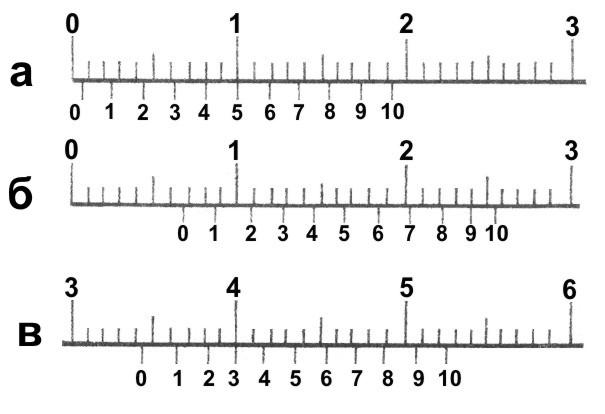
Рис.5.

См. также фото 1:

Фото 1: Смотрим шаг – 0,1 мм. Первая насечка стоит правее 2 см. Округляем до целых – 2 см (= 20 мм.) Далее смотрим, какая насечка совпадает со шкалой штанги. Совпадает пятая насечка, значит у нас 5 х 0,1 мм = 0,5 мм. Складываем с целой частью, получаем размер 20,5 мм. Если бы у нас совпала восьмая насечка, то было бы 20,8 мм. И так далее.

3. Микрометр

Микро́метр — универсальный инструмент (прибор), предназначенный для измерений линейных размеров абсолютным или относительным контактным методом в области малых размеров с низкой погрешностью (до 2 мкм), преобразовательным механизмом которого является микропара винт-гайка.

Основные элементы микрометра показаны на рис. 6.

Рис. 6. Гладкий микрометр МГ с пределом измерения 75—100 мм;

1 – скоба; 2 – пятка; 3 – микрометрический винт; 4 – стопор; 5 – стебель;
6 – барабан; 7 – трещотка.

Действие микрометра основано на перемещении винта вдоль оси при вращении его в неподвижной гайке. Перемещение пропорционально углу поворота винта вокруг оси. Полные обороты отсчитывают по шкале, нанесённой на стебле микрометра, а доли оборота – по круговой шкале, нанесённой на барабане. Оптимальным является перемещение винта в гайке лишь на длину не более 25 мм из-за трудности изготовления винта с точным шагом на большей длине. Поэтому микрометр изготовляют нескольких типоразмеров для измерения длин от 0 до 25 мм, от 25 до 50 мм и т. д. Предельный диапазон измерений наибольшего из микрометров заканчивается на отметке в 3000 мм. Для микрометров с пределами измерений от 0 до 25 мм при сомкнутых измерительных плоскостях пятки и микрометрического винта нулевой штрих шкалы барабана должен точно совпадать с продольным штрихом на стебле, а скошенный край барабана – с нулевым штрихом шкалы стебля. Для измерений длин, больших 25 мм, применяют микрометр со сменными пятками; установку таких микрометров на ноль производят с помощью установочной меры, прикладываемой к микрометру, или концевых мер. Измеряемое изделие зажимают между измерительными плоскостями микрометра. Обычно шаг винта равен 0,5 или 1 мм и соответственно шкала на стебле имеет цену деления 0,5 или 1 мм, а на барабане наносится 50 или 100 делении для получения отсчёта 0,01 мм. Эта величина отсчёта является наиболее распространённой, но имеются микрометры с отсчётом 0,005, 0,002 и 0,001 мм. Постоянное осевое усилие при контакте винта с деталью обеспечивается фрикционным устройством – трещоткой (храповиком). При плотном соприкосновении измерительных поверхностей микрометра с поверхностью измеряемой детали трещотка начинает проворачиваться с лёгким треском, при этом вращение микровинта следует прекратить после трёх щелчков.

При измерении детали сначала отсчитывается целое число миллиметров, а затем число на барабане, соответствующее сотым долям миллиметра.

Порядок проведения измерений

1. Измеряемый предмет устанавливается между пяткой и микрометрическим винтом, при этом вращая барабан, устанавливают шпиндель очень близко от предмета.

Замечание:держать инструмент следует левой рукой за изоляционную часть дуги, так чтобы тепло руки не меняло размер дуги и не нарушало точность измерений.

2. Шпиндель осторожно приближают до соприкосновения с измеряемым предметом.

Замечание:крутите против часовой стрелки (если смотреть с торца, где нарезка) барабан прибора, пока измеряемая деталь не зайдёт в зазор между измерительными торцами. Затем крутите по часовой стрелке до упора.

ВНИМАНИЕ! Закручивать надо только держа за нарезку на самом конце вращающегося барабана – тогда при упоре измерительных торцов в деталь эта часть барабана начнёт прокручиваться, издавая звук, как трещотка. Это значит, что измерительные торцы упёрлись в деталь и надо снимать показания. (Если крутить за большой барабан, то можно нечаянно перекрутить прибор и сорвать его.)

Замечание: для более точного определения размеров предмет следует закрепить.

3. Замеряем размер при помощи нониуса барабана в мм, который соответствует горизонтальному указательному штриху шкалы стебля.

4. Определяем общий размер замеряемого объекта.

5. Вращая барабан в обратном направлении, освободить предмет.

Отсчет показаний

Главная деталь микрометра – точный микрометрический винт, ввернутый в гайку, называемую стеблем. При одном обороте винт перемещается вдоль своей оси на 0,5 мм. На винте неподвижно насажен барабан, на котором по окружности нанесено 50 делений. Таким образом, поворот винта на одно деление равен 1/50 полного оборота, или 0,01 мм (0.5мм/50 = 0,01 мм).

Таким образом, цена деления микрометра С = 0,01 мм = 10^-5 м, точность отсчета Δх_пр. = ± 0,005 мм = ± 0,5•10^-5 м.

О погрешностях измерений

Виды измерений физических величин и их погрешностей

При измерении любой физической величины получить её абсолютно точное (истинное) значение невозможно из-за присутствующих всегда погрешностей измерений.

Различают прямые и косвенные измерения.

Измерение называютпрямым, если значение измеряемой величины (например, длины или массы предмета) находят в результате сравнения с мерой этой же величины (измерительной линейкой, гирями определенной массы) или считываются со шкалы прибора, используемого для проведения наблюдения (например, вольтметра при измерении электрического напряжения).

Измерение называюткосвенным, если значение измеряемой величины находят с помощью известной функциональной зависимости, которая связывает искомую величину с величинам, получаемыми непосредственно при прямых измерениях (например, сила электрического тока находится с помощью закона Ома по прямым измерениям электрического напряжения и сопротивления).

Все возможные погрешности измерений по характеру происхождения разделяют на три типа:

1. Грубая погрешность (промах) – чрезмерно большая погрешность, явно искажающая результат измерения.

Существует строгий математический способ определения ошибок подобного рода. Если подозрительное значение отличается от среднего более чем на 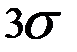( - среднеквадратическое отклонение среднего, смысл этой величины и способ вычисления даны ниже), то считаем его грубой ошибкой и вычеркиваем.

Эта погрешность, связанная с невнимательностью или ошибкой экспериментатора, исключается из протокола измерений. Имеет смысл измерение повторить.

2. Систематическая погрешность – погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.

Эта погрешность связана со сдвигом измеренного значения некоторой величины от её истинного значения. Если удается обнаружить причину или найти величину сдвига, то систематическую погрешность можно исключить введением поправки к измеренному значению величины. Однако, не существует универсальных правил, позволяющих найти систематическую погрешность данного измерения.

3. Случайные погрешности – погрешности, появление которых не может быть предупреждено.

Эти погрешности проявляются в разбросе отсчетов при повторных измерениях, проведенных в одних и тех же доступных контролю условиях, т.к. обусловлены факторами, меняющимися от измерения к измерению, действие которых на практике не всегда может быть учтено.

Выполнив измерение физической величины несколько раз, используя теорию погрешностей измерений, можно дать количественную оценку случайной погрешности и указать вероятность, с которой истинное значение измеряемой величины находится внутри некоторого интервала.

Методика статистической обработки результатов прямых измерений

Обозначим через 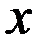измеряемую физическую величину. Пусть в результате нескольких опытов получено n пронумерованных значений 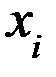(i – номер измерения, i = 1,2,3,…,n). Зададимся вопросом: Какую ошибку 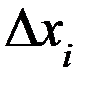мы допустили в каждом отдельном измерении? При известном истинном значение 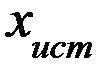, решение очевидно: .

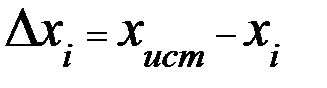Поскольку, 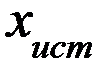нам не доступно, то его заменяют средним значением 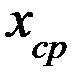, которое легко найти по известной формуле.

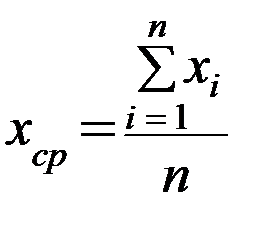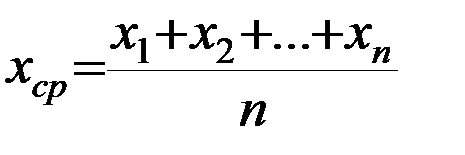или . (1)

Тогда, ошибка отдельного измерения ( 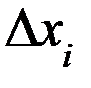) (несмотря на неизбежную небольшую неточность этих вычислений) легко вычисляется

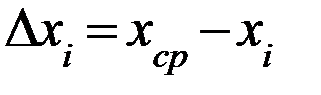(2)

Зная ошибку каждого измерения, следующим шагом найдем, так называемоесреднеквадратическое отклонение среднего :

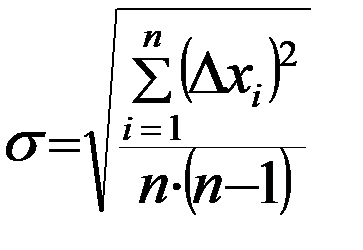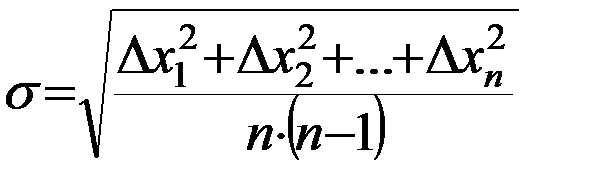или . (3)

(Внимание! Среднеквадратическое отклонение среднего вычисляют с точностью 10%-20%, не более 2 значащих цифр).

Формула для вычисления доказывается в теории вероятности. Для практических целей существенное значение имеет её смысловое наполнение. Отложим на оси всевозможных 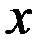, значения, , , .

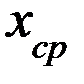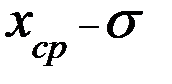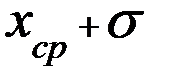x

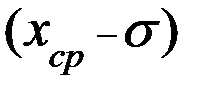
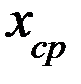
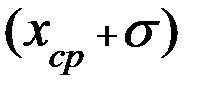
Оказывается, что при проведении новых серий экспериментов, следующие средние значения 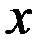будут попадать в интервал от ( 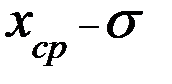) до ( 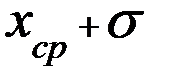) примерно 68 раз из 100. С точки зрения теории вероятности можно утверждать, что истинное значение 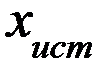лежит в интервале 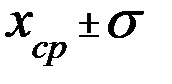с вероятностью 68%.

Вероятность 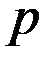, с которой среднее значение попадает в некоторый интервал, называется доверительной вероятностью, при этом интервал называют доверительным интервалом .

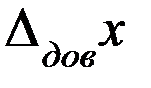Однако 68% невысокая вероятность. В подавляющем большинстве случаев требуется знать интервал с доверительной вероятностью 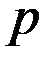= 90% , 95%, 98%. Найти его очень просто, если известны и специальные коэффициенты Стьюдента 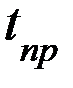, зависящие от числа измерений 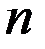и доверительной вероятности .

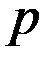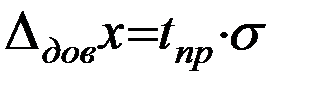(4)

Обработка случайных погрешностей прямых измерений сводится к нахождению 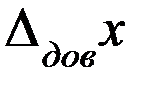с заданной доверительной вероятностью.

В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым 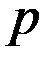= 0,95.

Таблица коэффициентов Стьюдента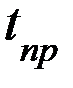

для доверительной вероятности 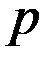= 0,95

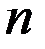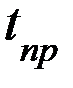	12,3	4,3	3,18	2,78	2,6	2,26

Полная погрешность измерений 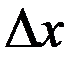складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу:

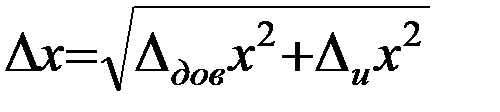(5)

Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:

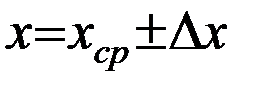, (6)

Рядом необходимо указать относительную погрешность

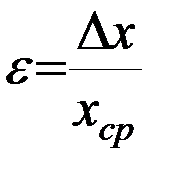, (7)

выраженную в процентах ( 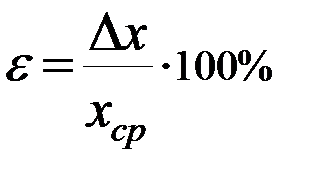) (8)

(Внимание! относительная погрешность ε превышающая 10%-15% свидетельствует о недостаточном усердии учащегося при выполнении лабораторной работы).

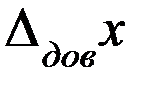Заметим, что и, следовательно, вычисляют с точностью порядка 10%–20%. Поэтому при вычислении полной ошибки удобно пользоваться следующим правилом: если одна из ошибок 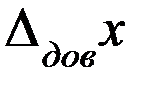или 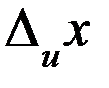превышает другую в 3 и более раз, то меньшей можно пренебречь.

Величину случайной погрешности можно уменьшить многократным повторением измерения. Использование теории случайных погрешностей оправдано лишь в том случае, если повторные измерения дают результаты, заметно отличающиеся друг от друга.

О точности измерительных приборов

Развитие измерительной техники привело к появлению разнообразных приборов, отличающихся своей точностью.

Точность прибора – это свойство измерительного прибора, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины.

Точность прибора либо задается классом точности[1] прибора, либо указана в паспорте, прилагаемом к прибору. Погрешность, вносимая прибором при каждом отдельном измерении (приборная погрешность, Δх_пр.), связана с точностью прибора. Эта погрешность равна той доле деления шкалы прибора, до которой с уверенностью в правильности результата можно производить отсчет.

В тех случаях, когда класс точности не указан и нет указаний в паспорте прибора, приборная погрешность принимается равной половине цены наименьшего деления шкалы прибора: Δх_пр. = ± 0,5C, где С – цена наименьшего деления шкалы прибора.

В том случае, когда приборная и случайная погрешности сравнимы по величине, полную погрешность измерений можно представить в виде суммы двух составляющих: Δх = Δх_случ. + Δх_пр..

Точность прибора невозможно превзойти никаким методом измерения на нем. Для более точных измерений применяют приборы более высокого класса.