Вектор плотности потока энергии волны. Поток энергии, переносимый волной через

Оглавление

Билет №1 ...................................................................................................................................................... 8

1. Преобразования Галилея. Инвариантность уравнений классической механики

относительно преобразований Галилея. ............................................................................................. 8

2. Основное уравнение молекулярно-кинетической теории идеального газа. ......................... 8

3. При изохорном нагревании кислорода объемом V=40 л давление газа изменилось на ∆p=

0,4 Мпа. Найти количество теплоты, сообщенное газу. .................................................................... 9

4. Шарик m=10 г летит со V0=100 м/с и ударяет шар, летящий ему навстречу со скоростью U0=10м/с. Определить массу шара, если удар абсолютно упругий. Скорости шарика и шара

после удара равны Vк=118 м/с, Uк=8 м/с. .......................................................................................... 9

Билет №2 ...................................................................................................................................................... 9

Вектор плотности потока энергии волны. Поток энергии, переносимый волной через

поверхность. ............................................................................................................................................ 9

Статистическое обоснование 2 начала тд. Формула Больцмана для статистической

энтропии. ............................................................................................................................................... 10

При какой температуре T средняя скорость атомов гелия станет равной первой

космической V1=7.93 км/с. ................................................................................................................. 11

4. Определить коэффициент диффузии и вязкости, среднюю длину свободного пробега молекул азота при давлении P=100 кПа и t= 57С. Как изменятся найденные величины в результате двукратного уменьшения объема газа при постоянной температуре?

Эффективный диаметр молекул азота d=0,37 нм. ........................................................................... 11

Билет №3 .................................................................................................................................................... 11

1. Энергия упругой волны. Объемная плотность энергии волны............................................... 11

2. Энтропия как функция состояния тд системы. 3 начало тд. ................................................... 12

Определить среднее значение полной кинетической энергии одной молекулы аргона,

азота и водяного пара при температуре Т=310К. ............................................................................. 13

4. Два моля неона охлаждаются от t1=180C до t2=50C. В процессе охлаждения давление газа изменяется по закону P=P₀exp(-T*/T)? T*=100K. Найти количество теплоты, отданное

газом при охлаждении. ....................................................................................................................... 13

Билет №4 .................................................................................................................................................... 13

1. Явления переноса в газах. Теплопроводность газов. .............................................................. 13

Статистическое обоснование 2 начала тд. Формула Больцмана для статистической

энтропии. ............................................................................................................................................... 15

3. Определите скорость нейтрона, если его кинетическая энергия равна Т=25 МэВ. ............. 15

4. Определите коэффициенты затухания двух диссипативных колебательных систем, если их резонансные частоты равны, а собственные частоты отличаются в 1,5 раза. При этом коэффициенты затухания отличаются в 2,2 раза, а частота одной из них равна 140 Гц. ............ 15

Билет №5 .................................................................................................................................................... 15

1. Закон сохранения механической энергии. ................................................................................ 15

2. Релятивистский закон сложения скоростей. ............................................................................. 16

3. Тепловая машина работает по прямому циклу 1-2-3-4-1, который состоит из изохоры 1-2, двух изобар 2-3 и 4-1, а также изотермы 3-4 с отдачей тепла холодильнику. При этом Р2=Р3<Р1=Р4. Изобразить этот цикл в переменных Р-V; P-T; V-T. .................................................. 17

4. Рабочее тело холодильной машины-азот, масса которого m=0,8 кг. Холодильная машина работает по обратному циклу Карно в интервале температур от Т1=263 К до Т2=573 К. найти количество теплоты, отбираемое от охлаждаемого тела, и работу внешних сил за цикл, если отношение максимального объема к минимальному равно 4. .................................................... 17

Билет № 6 ................................................................................................................................................... 17

1. Когерентные волны. Интерференция волн. Стоячая волна. ................................................... 17

2. Внутренняя энергия тд системы. Теплота и работа. Первое начало тд. ................................ 21

На какой высоте над поверхностью Земли атмосферное давление втрое меньше, чем на

ее поверхности? Температура воздуха =300 К и не изменяется с высотой. ................................. 22

4. Два физических маятника могут совершать малые колебания вокруг одной оси с частотами v1 и v2. Моменты инерции этих маятников относительно данной оси равны соответственно I1, I2. Маятники жестко соединили др с др. Определить период малых колебаний составного маятника. ....... 22

Билет № 7 ................................................................................................................................................... 22

1. Кинематические следствия из преобразований Лоренца. Относительность одновременности. Изменение продольных размеров тел. ........................................................... 22

2. Максвелловское распределение молекул по скоростям. ....................................................... 25

3. Определить среднюю и вероятную скорость молекул азота при t=300C. ............................ 27

Два моля одноатомного идеального газа нагреваются от 10С до 80С. В процессе

нагревания давление газа изменяется по закону P=P0exp(-T*/T), где T*=100K. Найти

количество теплоты, полученное газом при нагревании. ............................................................... 27

Билет № 8 ................................................................................................................................................... 27

Плоская гармоническая волна, длина волны, фазовая скорость, волновой вектор.

Сферическая волна. .............................................................................................................................. 33

2. Неравенство Клаузиуса. Тд энтропия. 3 начало тд. .................................................................. 34

3. Полная энергия релятив частицы возросла на Е=1,8 Дж. На сколько при этом изменится

ее кинетическая энергия? .................................................................................................................... 34

4. Два нейтрона движутся вдоль одной прямой со скоростями 0,9С и 0,8С. Определить скорость нейтронов относительно друг друга, если нейтроны движутся в одном направлении. 34

Билет № 11 ................................................................................................................................................. 34

1. Упругие волны в стержнях. Волновое уравнение. ................................................................... 34

2. Цикл Карно. Коэффициент полезного действия идеальной тепловой машины. ................ 36

Конический маятник состоит из нити длиной 1,2 м и прикрепленного к ней шарика.

Билет №1

1.Преобразования Галилея. Инвариантность уравнений классической механики относительно преобразований Галилея.

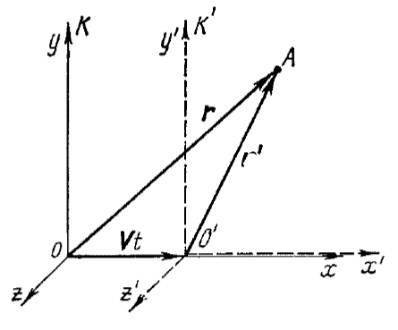Принцип относительности Галилея утверждает, что все инерциальные системы в механическом смысле эквивалентны, в них одинаковы свойства пространств и времени, законы механики имеют одинаковый вид во всех инерциальных системах отсчета. Пусть система К' движется относительно системы К поступательно с постоянной скоростью V. Время будем отсчитывать от момента, когда начала K и K’ систем отсчета совпадают. Тогда координаты и время некоторого события в системе К' будут выражаться через координаты и время в К с помощью преобразований Галилея:

r=r’+Vt, t=t’

В координатах:

x=x’+Vt; y=y’; z=z’; t=t’

Отсюда следует закон сложения скоростей:

v=v’+Vи неизменность ускорения: a=a’

При преобразованиях Галилея остаются неизменными расстояние между двумя любыми точками и их относительная скорость: ∆r=r2-r1=r’2-r’1, ∆v=v2-v1=v’2-v’1

Следовательно, не меняются силы взаимодействия между материальными точками. Кроме того, преобразования Галилея не меняют ускорения точки. Поэтому не изменяются обе части равенства, выражающего второй закон Ньютона, т. е. уравнение движения имеет одинаковый вид в разных системах отсчета (уравнение движения инвариантно относительно преобразований Галилея).

Преобразования Галилея основаны на утверждениях о независимости хода времени и длины отрезков от системы отсчета, которые считались неотъемлемыми свойствами пространства и времени. Теория относительности пересматривает представления о пространстве и времени и показывает, что преобразования Галилея верны только при V <<c.

2.Основное уравнение молекулярно-кинетической теории идеального газа.

Рассмотрим столкновение молекул идеального газа со стенкой сосуда. Ось X направлена к стенке перпендикулярно к ней. Пусть в единице объема n1 молекул имеют проекцию скорости на ось X близкую к значению Vx1 , n2 молекул имеют скорость V2x и так далее. Тогда за время t со стенкой столкнутся N1  n1Vx1tS молекул «первого сорта». Их импульс изменится на величину  n1V_x1tS2m₀V_x1 .

Общее изменение импульса всех молекул разного сорта, столкнувшихся со стенкой равен

𝑛1𝑉𝑥21+𝑛2𝑉𝑥22+⋯

∆p_x= -2 m₀tSn( )

𝑛

При суммировании мы учитываем только те молекулы, которые летят к стенке. Очевидно общее число таких молекул в единице объема n/2. Ясно, что

Отсюда получим давление

(1)

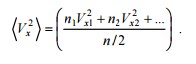
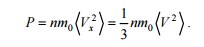
Эту формулу можно переписать в виде p=2/3*n<E>, где <E>=m<V²>/2- средняя кинетическая энергия поступательного движения молекул. Формулу (1) называют основным уравнением кинетической теории газов. Она раскрывает физический смысл давления: давление газа на стенку определяется средним значением кинетической энергии поступательного движения молекул.

3. При изохорном нагревании кислорода объемом V=40 л давление газа изменилось на ∆p= 0,4 Мпа. Найти количество теплоты, сообщенное газу.

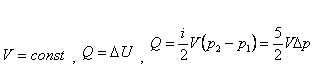
4. Шарик m=10 г летит со V0=100 м/с и ударяет шар, летящий ему навстречу со скоростью U0=10м/с. Определить массу шара, если удар абсолютно упругий. Скорости шарика и шара после удара равны Vк=118 м/с, Uк=8 м/с.

Билет №2

1.Вектор плотности потока энергии волны. Поток энергии, переносимый волной через поверхность.

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии Ф через поверхность. Поток энергии-скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т.е. совпадает с размерностью мощности (эрг/с, ватты).

Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

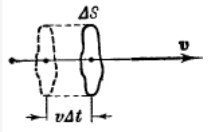
Пусть через площадку ∆S, перпендикулярно к направлению распространения волны, переносится за время ∆t энергия ∆E. Тогда плотность потока энергии j по определению равна: j=∆Ф/∆S (∆Ф=∆Е/∆t) (1)

Через площадку ∆S (см рис) за время ∆t будет перенесена энергия, заключенная в объеме цилиндра с основание ∆S и высотой v∆t (v-фазовая скорость волны). Если размеры цилиндра достаточно малы для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то ∆Е=u∆Sv∆t (u- плотность энергии=1/2ᵨa²ω²). Подставив в (1): j=uv. Рассматривая фазовую скорость как вектор, направление которого совпадает с направление распространения волны: j=uv- вектор плотности потока энергии (введен Умовым).

Зная j в любой точке произвольной поверхности S, можно вычислить поток энергии Ф через эту поверхность. С этой целью разобьем поверхность на элементарные участки ∆S, столь малые, чтобы каждый из них можно было считать плоским, а вектор j в пределах каждого ∆S постоянным, тогда ∆Ф=j_n∆S (j_n=jcosα, угол между n к ∆S и вектором j). Полный поток: Ф=∫_𝑆 jn 𝑑𝑆

2.Статистическое обоснование 2 начала тд. Формула Больцмана для статистической энтропии.

тд вероятность состояния- число различных способов, которыми может быть осуществлено данное состояние.

Предоставленная самой себе система будет переходить из менее вероятных состояний в более. Второе начало, указывающее на необратимость перехода работы в тепло, обусловлено тем, что переход теплоты в работу означает переход от более вероятного состояния к менее вероятному.

Пусть в сосуде 6 молекул газа. Разделим мысленно его на 3 равные части. Хаотически перемещаясь, молекулы создают определенные

макрораспределения. Тд вероятностьчисло N частиц по n состояниям (6 частиц 3 состояния), определяется формулой W=N!/N1!N2!...Nn! Наибольшая W у равномерного распределения, оно может осуществляться наибольшим числом способов. Все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния.

3. При какой температуре T средняя скорость атомов гелия станет равной первой космической V1=7.93 км/с.

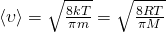
4. Определить коэффициент диффузии и вязкости, среднюю длину свободного пробега молекул азота при давлении P=100 кПа и t= 57С. Как изменятся найденные величины в результате двукратного уменьшения объема газа при постоянной температуре? Эффективный диаметр молекул азота d=0,37 нм.

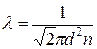
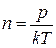
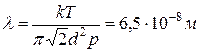
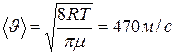
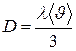
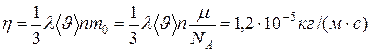
При уменьшении изотермически объема давление возрастает во столько же-> коэф диф уменьшится, вязкости не изменится.

Билет №3

1. Энергия упругой волны. Объемная плотность энергии волны.

Выделим в среде, в которой распространяется волна, элементарный объем ∆V, настолько малый, чтобы деформации и скорости движения во всех точках этого объема можно было считать одинаковыми и равными, соответственно, ∂ᶓ/∂x и ∂ᶓ/∂t. Выделенный нами объем будет обладать потенциальной энергией упругой деформации

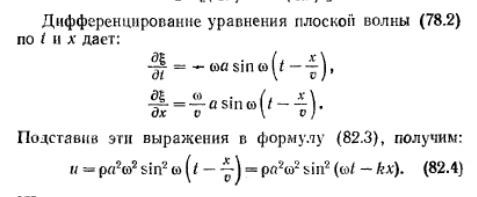
2. Энтропия как функция состояния тд системы. 3 начало тд.

Понятие энтропии ввел Клаузиус. Энтропия вводится через ее элементарное приращение в виде формулы

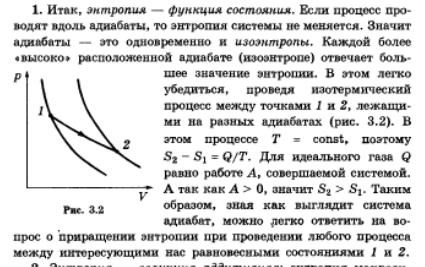dS Q/T (1)

В отличие от теплоты, энтропия является такой же функцией состояния как температура, внутренняя энергия или давление. Полученное системой тепло зависит от процесса перехода из начального состояния в конечное. Вместе с тем, приращение энтропии S  S2  S1 не зависит от процесса, а только от начального и конечного состояний. В интегральной форме соотношение

(1) принимает вид

S 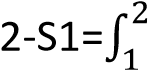𝑄/𝑇

Важно, чтобы состояния 1 и 2 были равновесными, а расчет по формуле (2) может проводиться по любому обратимому процессу между состояниями 1 и 2. Введенная таким образом энтропия S определена с точностью до произвольной аддитивной постоянной.

3 начало: при стремлении абсолютной температуры к нулю энтропия любого тела так же стремится к нулю lim 𝑆=0 𝑇→0

Теперь можно вычислять не только приращение энтропии, но и саму ее величину:

𝑇 𝐶𝑝(𝑇)𝑑𝑇

S(p,T)=∫_{0 𝑇}

Отсюда следует, что при T  0 теплоемкость всех макросистем должна стремиться к нулю, иначе интеграл будет стремиться к бесконечности.

3. Определить среднее значение полной кинетической энергии одной молекулы аргона, азота и водяного пара при температуре Т=310К.

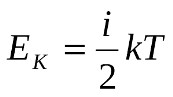азот: i=5 (3поступ+2вращ); аргон: i=3; пар: i=6 (3поступ+3вращ) k=1.38*10^-23Дж/К

4. Два моля неона охлаждаются от t1=180C до t2=50C. В процессе охлаждения давление газа изменяется по закону P=P₀exp(-T*/T)? T*=100K. Найти количество теплоты, отданное газом при охлаждении.

Билет №4

1.Явления переноса в газах. Теплопроводность газов.

Выведенная из состояния равновесия, любая макросистема стремиться вернуться в равновесное состояние. При этом растет энтропия, значит этот процесс не обратим. Нарушение равновесия сопровождается возникновением потоков или частиц, или тепла, или электрического заряда и др. Соответствующие процессы называют явлениями переноса. Все они являются необратимыми.

Три явления переноса: диффузия, внутреннее трение и теплопроводность.

Поток-величина скалярная и алгебраическая, знак зависит от выбора положительного «направления»: с одной стороны поверхности S к другой или наоборот.

Любое явление переноса связано с неодинаковостью в пространстве некоторой величины (например, температура). Локальное равновесие-состояние, в котором среда в каждой малой части своего объема (объем, размер которого намного превышает среднее расстояние между соседними молекулами, число частиц в нем должно быть макроскопическим) находится в тепловом равновесии, однако равновесие между различными частями отсутствует.

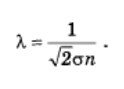
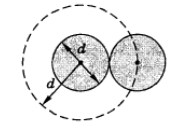Эффективный диаметр молекулы-расстояние d, на которое сближаются центры 2 молекул при столкновении. Площадь, ограниченная штриховой окружностью на рис, называют эффективным сечением молекулы: σ=∏d² Средняя длина свободного пробега:

В явлении теплопроводности величиной G является средняя энергия теплового движения, приходящаяся на одну молекулу. Из теоремы о равнораспределении энергии по степеням свободы имеем G=(i/2)kT, и тогда плотность потока тепла

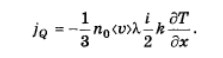
Учитывая, что (i/2)kn₀=c_vᵨ имеем:

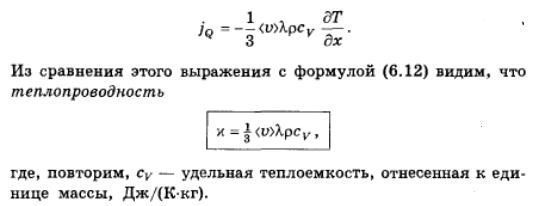
2. Статистическое обоснование 2 начала тд. Формула Больцмана длястатистической энтропии.

3. Определите скорость нейтрона, если его кинетическая энергия равна Т=25 МэВ.

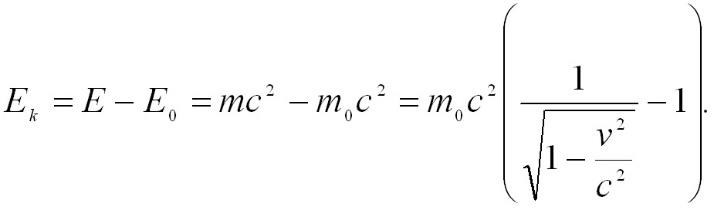
M0=1,67*10^-23; c= 3*10^8; Ek=4*10^-12 Дж

4. Определите коэффициенты затухания двух диссипативных колебательных систем, если их резонансные частоты равны, а собственные частоты отличаются в 1,5 раза. При этом коэффициенты затухания отличаются в 2,2 раза, а частота одной из них равна 140 Гц.

Ωрез= sqrt(ω0^2-2β^2)

Билет №5

1.Закон сохранения механической энергии.

Консервативные силы. Сила взаимодействия между точками называется консервативной, если работа этой силы зависит только от начального и конечного положения точек, но не зависит от траектории их перемещения. Силы, не удовлетворяющие этому условию, называют неконсервативными.

Механическая энергия системы определяется как сумма ее кинетической энергии и потенциальной энергий: Eмех  Ek U . Потенциальная энергия включает в себя потенциальную энергию взаимодействия между частицами системы и потенциальную энергию частиц системы во внешнем поле.

Изменение механической энергии. Изменение кинетической энергии равно работе всех сил, приложенных к точкам системы: Ek 2  Ek1  Aвсех сил . Изменение потенциальной энергии равно работе всех консервативных сил (внутренних и внешних, включая работу потенциальных полей), взятой с обратным знаком: U2 U1  Aконс . Кроме консервативных сил могут действовать и неконсервативные, суммарную работу которых обозначим Aнеконс . Тогда:

Ek 2  Ek1  Aвсех сил  Aконс  Aнеконс  U2 U1  Aнеконс .

Значит, изменение механической энергии равно работе всех неконсервативных сил, как внешних, так и внутренних: (Ek2 U2)  (Ek1 U1)  Eмех  Aнеконс

Закон сохранения механической энергии: механическая энергия замкнутой системы, в которой действуют только консервативные силы, остается постоянной.

2. Релятивистский закон сложения скоростей.

Пусть в K-СО в плоскости x, y движется частица со скоростью υ, проекции которой υx и υy . Найдем при помощи преобразований Лоренца проекции скорости этой частицы ' υx и ' υy в K’ системе, движущейся со скоростью V вдоль оси x:

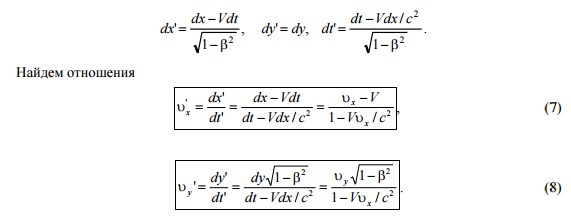
Эти формулы выражают релятивистский закон преобразования скорости. При малых скоростях (V

<< c и c υx << ) они переходят в формулы преобразования скорости ньютоновской механики

vx ' = vx –V, vy = vy ' .

И, наконец, проверим непосредственно, что релятивистские формулы соответствуют утверждению второго постулата Эйнштейна относительно неизменности скорости света во всех инерциальных системах отсчета. Пусть вектор cимеет в K-СО проекции cx и cy, то есть c²=c_x²+c_y² . Тогда в K’-СО получим

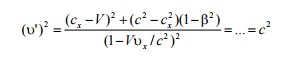
3. Тепловая машина работает по прямому циклу1-2-3-4-1, который состоит из изохоры 1-2, двух изобар 2-3 и 4-1, а также изотермы 3-4 с отдачей тепла холодильнику. При этом Р2=Р3<Р1=Р4. Изобразить этот цикл в переменных Р-V;

P-T; V-T.

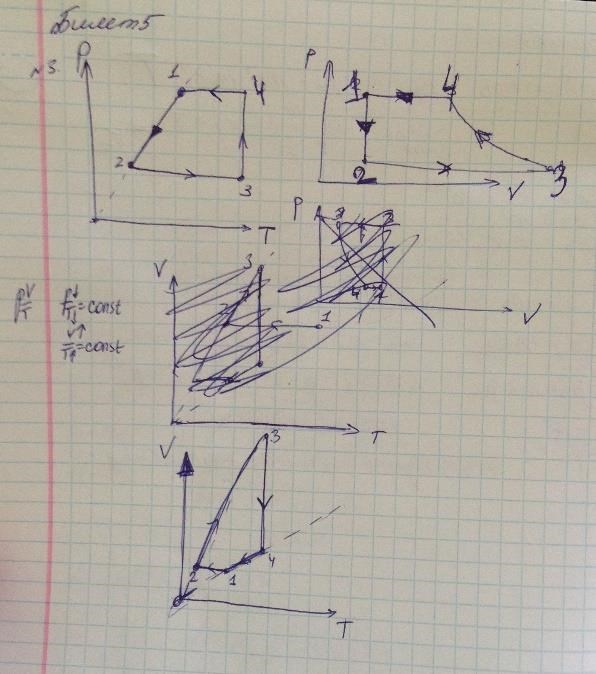
4. Рабочее тело холодильной машины-азот, масса которого m=0,8 кг. Холодильная машина работает по обратному циклу Карно в интервале температур от Т1=263 К до Т2=573 К. найти количество теплоты, отбираемое от охлаждаемого тела, и работу внешних сил за цикл, если отношение максимального объема к минимальному равно 4.

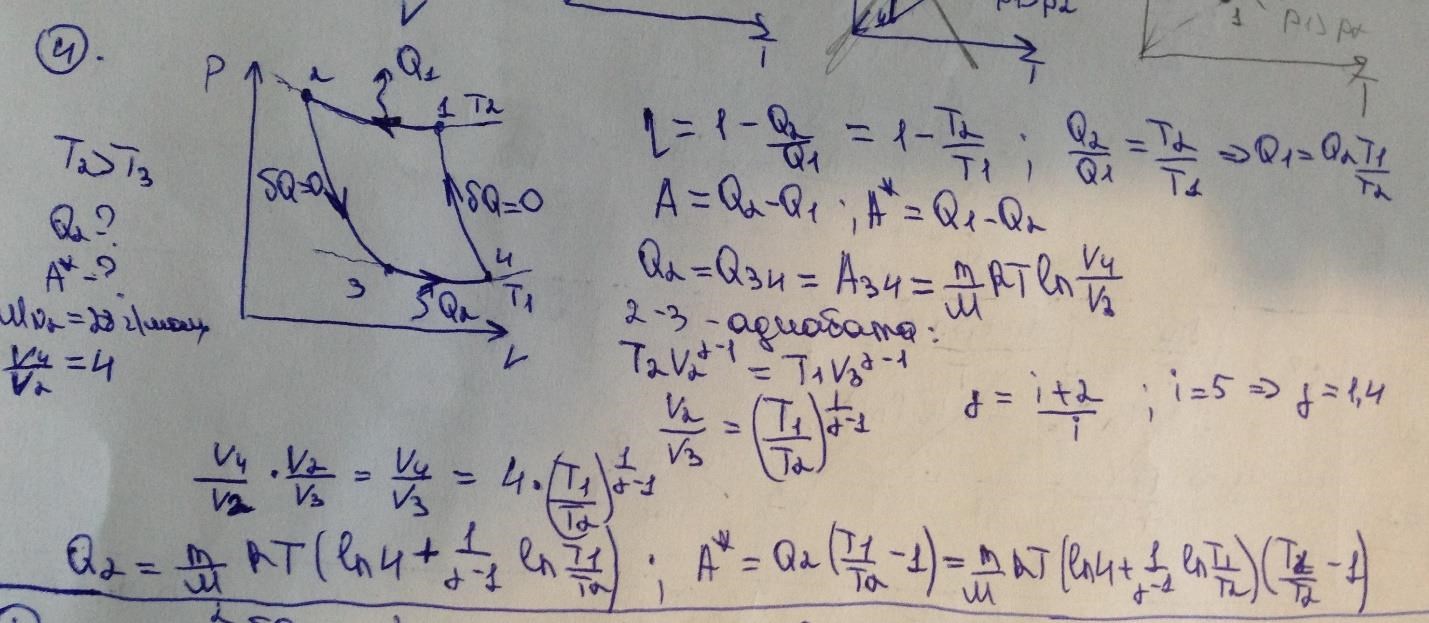
Билет № 6

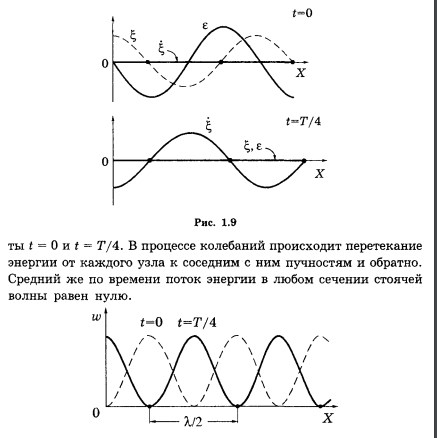
1. Когерентные волны. Интерференция волн. Стоячая волна.

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. Могут быть лишь волны с одинаковой частотой. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других ослабляют друг друга.

Рассмотрим 2 волны, распространяющихся от точечных источников О1 и О2, колеблющихся с постоянной разностью фаз (когерентные источники). Определим результирующее колебание в к-л точке среды при условии, что оба колебания, вызываемые каждой из волн в отдельности, имеют одинаковое направление (расстояние между источниками << расстояния от источников до точки).

2. Внутренняя энергия тд системы. Теплота и работа. Первое начало тд.

Внутренняя энергия макросистемы равна сумме кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия молекул между собой и внутренней энергии самих молекул. Внутренняя энергия не включает потенциальную энергию системы во внешних полях и кинетическую энергию системы как целого. Внутренняя энергия U является функцией состояния системы и не зависит от того, каким путем мы привели систему в данное состояние. Приращение внутренней энергии определяется только конечным и начальным состояниями и не зависит от процесса, который перевел систему из одного состояния в другое.

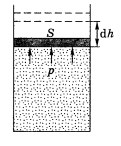
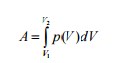Работа, совершаемая макросистемой. Рассмотрим сначала макросистему в виде газа в цилиндрическом сосуде под поршнем. При малом перемещении поршня на dh газ совершает работу A  Fdh  pSdh  pdV , где dV - приращение объема, S - площадь поршня. Так как работа не является функцией состояния, то бесконечно малая работа обозначена A, чтобы отличить ее от бесконечно малого изменения функции (дифференциала). Итак A  pdV , (2) При перемещении поршня давление может изменяться. Поэтому работа газа при конечном изменении объема от V1 до V2 равна

Формулы (2), (3) справедливы не только для газов, но и для других простых систем, например, для жидкостей. На графике p, V работа численно равна площади под графиком, и эта площадь зависит от вида кривой, то есть от процесса.

Количество теплоты. В отличие от механической энергии, которая может изменяться только за счет работы, внутренняя энергия может изменяться как за счет работы, так и при контакте с телами, имеющими другую температуру, т.е. в процессе теплообмена. Энергия, переданная при теплообмене (подведении тепла), называется количеством теплоты или теплотой и обозначается Q. Теплота считается положительной, если система получает энергию, и отрицательной, если отдает.

Первое начало термодинамики утверждает: приращение внутренней энергии макросистемы равно сумме совершенной над системой работы всех внешних сил и количества переданного системе тепла:

U2 U1  Q  A' . (4)

Для квазистатических процессов A' A, где A - работа, производимая самой системой над внешними телами. В этом случае первое начало термодинамики переписывается в виде:

Q  U  A (5)

Все входящие в (4) величины являются алгебраическими, то есть могут быть как положи- тельными, так и отрицательными: если Q  0 , то тепло подводится к системе, если A  0 , то система совершает положительную работу над внешними телами, если U  0 , то U2 U1 . Первое начало ТД в дифференциальном виде имеет вид

Q  dU  A. (6)

( Q - не приращение какой-либо функции, а элементарное (малое) количество теплоты в данном процессе). Используя уравнение (2), запишем первое начало термодинамики для простой системы, получившей бесконечно малое количество теплоты:

Q  dU  pdV (7)

Иногда формулируют как невозможность создания вечного двигателя первого рода (который производил бы работу из ничего).

3. На какой высоте над поверхностью Земли атмосферное давление втрое меньше, чем на ее поверхности? Температура воздуха =300 К и не изменяется с высотой.

4. Два физических маятника могут совершать малые колебания вокруг одной оси с частотами v1 и v2. Моменты инерции этих маятников относительно данной оси равны соответственно I1, I2. Маятники жестко соединили др с др. Определить период малых колебаний составного маятника.

Билет № 7

1.Кинематические следствия из преобразований Лоренца. Относительность одновременности. Изменение продольных размеров тел.

Кинематические следствия: 1) относительность понятия одновременности; 2) релятив-ое замедление времени; 3) Лоренцево сокращение длины.

Относительность одновременности. Пусть в K-СО происходят два каких-то события A1 (x1, y1,z1,t1) и A2 (x2, y2, z2, t2). Найдем время между этими событиями в K’-СО, движущейся со скоростью V вдоль оси x. Из преобразований Лоренца получим

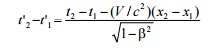
Отсюда следует, что события одновременные в K-СО, не одновременны в K’-СО. Исключением является случай, когда оба события происходят в K-системе одновременно в одной точке (в точках с одинаковыми координатами x). Тогда эти события одновременны и в любой другой инерциальной СО. Итак, одновременность – понятие относительное. События одновременный в одной СО, в общем случае не одновременны в другой СО.

Замедление времени. Рассмотрим сначала эффект замедления времени на специальном примере, а затем получим общую формулу из преобразований Лоренца.

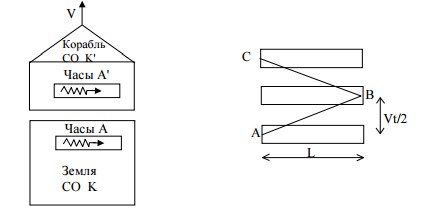
Пусть космический корабль (система K') движется относительно Земли (система K) со скоростью V. На Земле и на корабле есть одинаковые часы, например, световые часы. Свет отражается от оснований цилиндра: часы "тикают". Пусть часы A' один раз "тикнули", то есть световой импульс прошел расстояние 2L в K' системе. Соответствующее время в K' системе t0= 2L/ c.

Наблюдатель в СО K "увидит" картину, изображенную на правом рисунке, и отсчитает время t по своим часам A. Время t во столько раз больше t0, во сколько раз ABC больше 2L:

Время t0 называют собственным временем. Это время между двумя событиями, которые наблюдатель видит в одной и той же точке пространства, то есть время, измеренное наблюдателем, движущимся вместе с часами. Собственное время t0 меньше времени, измеренного неподвижным наблюдателем, для которого события происходят в разных точках пространства. Этот эффект называют замедлением времени: с точки зрения неподвижного наблюдателя время в быстро движущемся относительно него космическом корабле течет медленнее (движущиеся относительно наблюдателя часы идут медленнее, чем неподвижные).

Получим теперь формулу (6) из преобразований Лоренца. Пусть в некоторой фиксированной точке x’ системы K’ протекает некоторый процесс (например, рождение и распад частицы) длительностью Δt0 = t’2 –t’1 (собственное время). Найдем длительность этого процесса

Δt = t2 – t1 в K системе, относительно которой K’ система движется со скоростью V. Из преобразований Лоренца получим

Сокращение длины. Длина тела относительна, то есть зависит от того, в какой СО она измеряется. Пусть стержень покоится в СО K’. Его длина l0 получается путем откладывания вдоль стержня единичного масштаба (эталона длины), покоящегося относительно этого стержня. Длину l0 называют собственной длиной стержня. Если стержень движется относительно СО K, то описанная процедура измерения его длины не годится. Для определения длины стержня l в этом случае нужно отметить неподвижными метками A и B положения концов движущегося стержня в рассматриваемой СО в один и тот же момент времени. Расстояние между этими неподвижными точками и будет, по определению, длиной движущегося стержня l. Длиной движущегося стержня в покоящейся СО называется расстояние между двумя точками в этой системе, мимо которых концы стержня проходят одновременно. Если взять другую СО, то, ввиду относительности одновременности, концы стержня пройдут в этой СО мимо точек A и B, вообще говоря, не одновременно. Роль A и B будут играть другие точки A' и B', неподвижные в новой СО. Расстояние между этими точками будет иным. Таким образом, как и промежутки времени, длины отрезков также относительны. Найдем длину движущегося вдоль оси x стрежня при помощи преобразований Лоренца. Пусть стержень покоится в СО K'. Тогда разность координат его концов в системе K' есть собственная длина l0. Разность же координат тех же концов x2 - x1 в "неподвижной" СО K, взятая в один и тот же момент времени t, будет длиной движущегося стержня l. Тогда из преобразований Лоренца следует

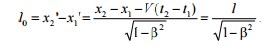
Таким образом, длина l движущегося стержня оказывается меньше его собственной длины l0, и в разных системах отсчета она будет иметь свое значение.

2. Максвелловское распределение молекул по скоростям.

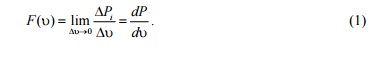
3. Определить среднюю и вероятную скорость молекул азота при t=300C.

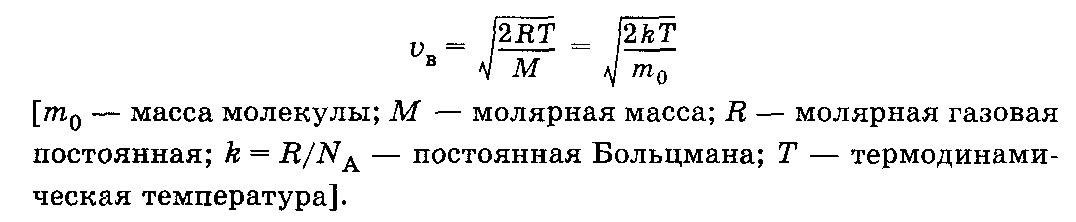
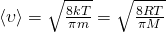
4. Два моля одноатомного идеального газа нагреваются от 10С до 80С. Впроцессе нагревания давление газа изменяется по закону P=P0exp(-T*/T), гдеT*=100K. Найти количество теплоты, полученное газом при нагревании.

Билет № 8

1. Основное уравнение релятивистской динамики. Связь между импульсом и энергией релятивистской частицы.

Второй закон Ньютона в релятивистском случае имеет вид (1)

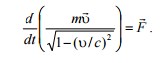
где v- скорость частицы (материальной точки), m - ее масса – не зависящая от скорости и выбора инерциальной системы отсчета характеристика частицы. Величину

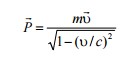
называют релятивистским импульсом частицы. Тогда второй закон Ньютона приобретает формально такой же вид, что и в классической механике.

Замечание-1. Уравнение (1) не допускает движения со скоростью большей скорости света.

Замечание-2. Уравнение (1) справедливо во всех инерциальных системах отсчета, однако сила не является инвариантной величиной: ее величина и направление в разных системах отсчета могут быть различными.

2. Интерференция волн. Стоячая волна.

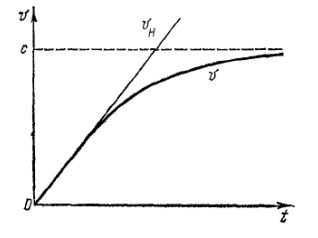
3. Работа тепловой машины = 6 кДж. Определить температуру нагревателя t1, если температура холодильника t2=0С, а КПД =0,6 max возможного КПД при затрате количества теплоты Q1=8 кДж. (просто)

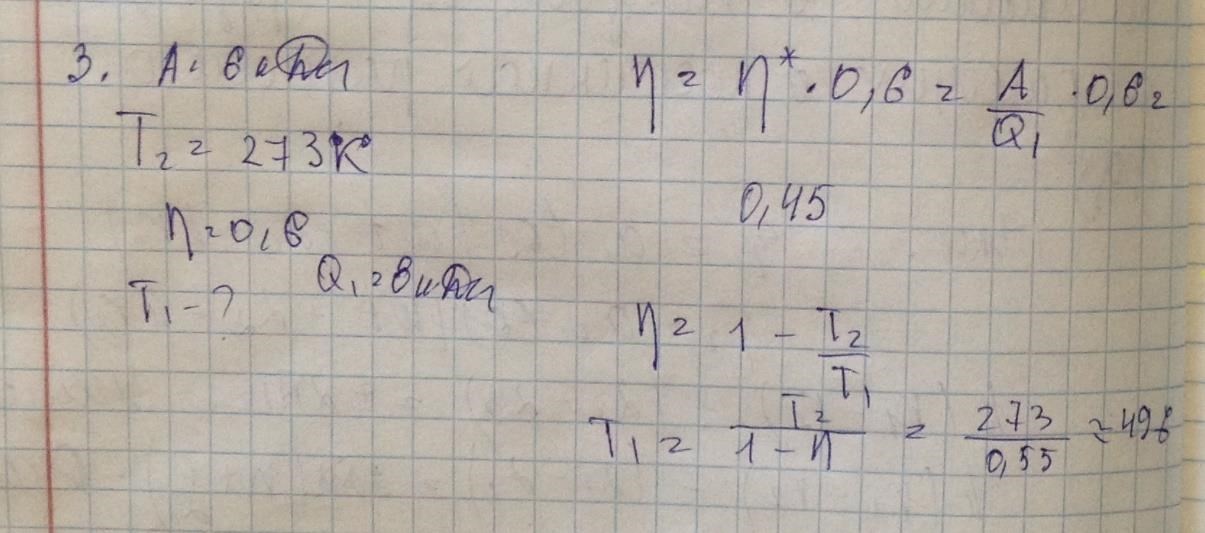
4. В результате изохорного нагревания азота массой m=8г давление газа увеличилось в 3 раза. Определить изменение энтропии газа.

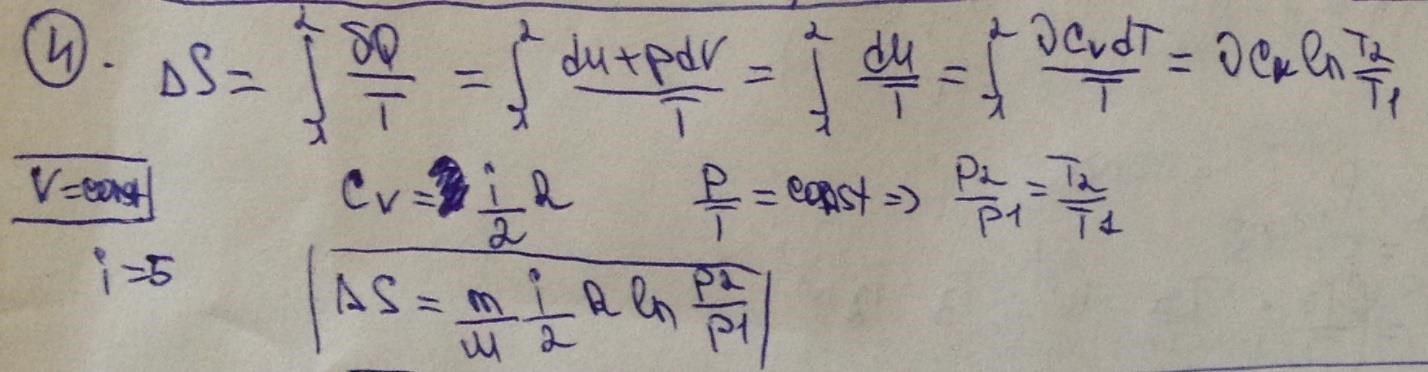
Билет № 9

1.СТО. Постулаты Эйнштейна. Преобразования Лоренца.

Теория относительности - фундаментальная физическая теория, охватывающая всю физику.

Создана А. Эйнштейном в 1905 г. Большой вклад в ее создание внесли Лармор, Лоренц, Пуанкаре. Механика Ньютона (классическая механика) следует из теории относительности (релятивистской механики) в предельном случае малых по сравнению со скоростью света скоростей, как частный случай.

Первый постулат: Принцип относительности: все процессы природы протекают одинаково во всех инерциальных СО. Это означает, что во всех инерциальных СО физические законы имеют одинако