Реальные газы, жидкости и твердые тела

· Уравнение Ван-дер-Ваальса для одного моля газа

,

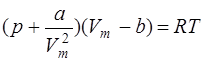для произвольного количества вещества ν газа

,

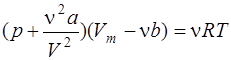где а и b – постоянные Ван-дер-Ваальса (рассчитанные на один моль газа); V – объём, занимаемый газом; V_m – молярный объём;

p - давление газа на стенки сосуда.

Внутреннее давление, обусловленное силами взаимодействия молекул,

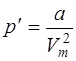, или .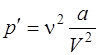

· Связь критических параметров – объёма, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:

; ;

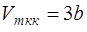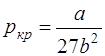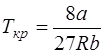
· Внутренняя энергия реального газа

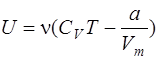
где С_V –молярная теплоёмкость газа при постоянном объёме.

· Поверхностное натяжение

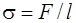
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкость, или

,

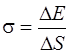где ∆E – изменение свободной энергии поверхностной плёнки жидкости, связанное с изменением площади ∆S – поверхности этой плёнки.

· Формула Лапласа в общем случае записывается в виде

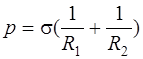
где p-давление, создаваемое изогнутой поверхностью жидкости; σ - поверхностное натяжение; R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных сечений жидкости, а в случае сферической поверхности

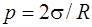
· Высота подъёма жидкости в капилярной трубке

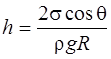
где θ – краевой угол; R-радиус канала трубки; ρ-плотность жидкости; g-ускорение свободного падения.

· Высота подъёма жидкости между двумя близкими и параллельными плоскостями

,

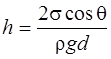где d- расстояния между плоскостями.

· Закон Дюлонга и Пти

C_V = 3R,

где C_V – молярная (атомная) теплоемкость химически простых твердых тел.

8.1. Кислород (ν = 10 моль) находится в сосуде объемом V = 5 л. Определить: 1) внутреннее давление газа; 2) собственный объем молекул Поправки а и b принять равными соответственно 0,136 Н^.м⁴/моль² и 3,17^.10^-5 м³/моль. Ответ: 1) 544 кПа; 2) 79,3 см³.

8.2. Углекислый газ массой 6,6 кг при давлении 0,1 МПа занимает объем 3,75 м³. Определить температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправки a и b принять равными соответственно 0,361 Н^.м⁴/моль² и 4,28^.10^-5 м³/моль. Ответ: 1) 302 К; 2) 301 К.

8.3. Углекислый газ массой 2,2 кг находится при температуре 290 К в сосуде вместимостью 30 л. Определить давление газа, если: 1) газ реальный; 2) газ идеальный. Поправки a и b принять равными соответственно 0,361 Н^.м⁴/моль² и 4,28^.10^-5 м³/моль. Ответ: 1) 3,32 МПа; 2) 4,02 МПа.

8.4. Плотность азота ρ = 140 кг/м³, его давление P = 10 МПа. Определить температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправки a и b принять равными соответственно 0,135 Н^.м⁴/моль² и 3,86^.10^-5 м³/моль. Ответ: 1) 260 К; 2) 241 К.

8.5. Азот (ν = 3 моль) расширяется в вакуум, в результате чего объем газа увеличивается от V₁ = 1 л до V₂ = 5 л. Какое количество теплоты Q необходимо сообщить газу, чтобы его температура осталась неизменной? Поправку a принять равной 0,135 Н^.м⁴/моль². Ответ: 972 Дж.

8.6. Углекислый газ массой 88 г занимает при температуре 290 К объем 1000 см³. Определить внутреннюю энергию газа, если: 1) газ идеальный; 2) газ реальный. Поправку а принять равной 0,361 Н^.м⁴/моль². Ответ: 1) 14,5 кДж; 2) 13 кДж.

8.7. Кислород (ν = 2 моль) занимает объем V₁ = 1 л. Определить изменение температуры кислорода, если он адиабатически расширяется в вакууме до объема V₂ = 10 л. Поправку a принять равной 0,136 Н^.м⁴/моль². Ответ: –11,8 К.

8.8. Азот (ν = 2 моль) адиабатически расширяется в вакуум. Температура газа при этом уменьшается на 1 К. Определить работу, совершаемую газом против межмолекулярных сил притяжения. Ответ: 83,1 Дж.

8.9. Кислород (ν = 1 моль) (реальный газ), занимавший при T₁ = 400 К объем V₁ = 1 л, расширяется изотермически до V₂ = 2V₁. Определить: 1) работу при расширении; 2) изменение внутренней энергии газа. Поправки a и b принять равными соответственно 0,136 Н·м⁴/моль² и 3,17·10^-5 м³/моль. Ответ: 1) 2,29 кДж; 2) 68 Дж.

8.10. Определить радиус R капли спирта, вытекающей из узкой вертикальной трубки радиусом r = 1 мм. Считать, что в момент отрыва капля сферическая. Поверхностное натяжение спирта σ = 22 мН/м, а его плотность ρ = 0,8 г/см³. Ответ: 1,61 мм.

8.11. Давление воздуха внутри мыльного пузыря на ΔP = 200 Па больше атмосферного. Определить диаметр d пузыря. Поверхностное натяжение мыльного раствора σ = 40 мН/м. Ответ: 1,6 мм.

8.12. Воздушный пузырек диаметром d = 0,02 мм находится на глубине h = 25 см под поверхностью воды. Определить давление воздуха в этом пузырьке. Атмосферное давление принять нормальным. Поверхностное натяжение воды σ = 73 мН/м, а ее плотность ρ = 1 г/см³. Ответ: 118 кПа.

8.13. Вертикальный капилляр погружен в воду. Определить радиус кривизны мениска, если высота столба воды в трубке h = 20 мм. Плотность воды ρ = 1 г/см³, поверхностное натяжение σ = 73мН/м. Ответ: 744мкм.

8.14. Широкое колено U-образного манометра имеет диаметр d₁ = 2 мм, узкое – d₂ = 1 мм. Определить разность Δh уровней ртути в обоих коленах, если поверхностное натяжение ртути σ = 0,5 Н/м, плотность ртути ρ = 13,6 г/см², а краевой угол θ = 138°. Ответ: 5,6 мм.

8.15. Используя закон Дюлонга и Пти, определить удельную теплоемкость: 1) натрия; 2) алюминия. Ответ: 1) 1,08 кДж/(кг·К); 2) 0,924 кДж/(кг·К).

8.16. Пользуясь законом Дюлонга и Пти, определить, во сколько раз удельная теплоемкость железа больше удельной теплоемкости золота. Ответ: 3,52.

8.17. Для нагревания металлического шарика массой 10 г от 20 до 50 °С затратили количество теплоты, равное 62,8 Дж. Пользуясь законом Дюлонга и Пти, определить материал шарика. Ответ: Олово, так как М = 0,119 кг/моль.

8.18. Изменение энтропии при плавлении 1 моль льда составило 25 Дж/К. Определить, насколько изменится температура плавления льда при увеличении внешнего давления на 1 МПа? Плотность льда ρ₁ = 0,9 г/см³, воды ρ₂ = 1 г/см³. Ответ: ΔT = –0,08 К.

Литература

1. Волькенштейн В.С. Сборник задач по курсу физики. – СПб.: СпецЛит, 2001.

2. Трофимова Т.И. Сборник задач по курсу физики для втузов. – М.: «Оникс 21 век», «Мир и Образование», 2003.

3. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл-пресс, 1977.

Индивидуальные задания.

Тема 1. Кинематика

	1.1, 1.31, 1.10		1.11, 1.27, 1.17		1.21, 1.3, 1.37
	1.2, 1.32, 1.11		1.12, 1.26, 1.18		1.22, 1.4, 1.36
	1.3, 1.33, 1.12		1.13, 1.25, 1., 2		1.23, 1.5, 1.35
	1.4, 1.34, 1.20		1.14, 1.24, 1.3		1.24, 1.6, 1.34
	1.5, 1.35, 1.21		1.15, 1.23, 1.4		1.25, 1.7, 1.33
	1.6, 1.36, 1.22		1.16, 1.22, 1.5		1.26, 1.8, 1.32
	1.7, 1.37, 1.23		1.17, 1.21, 1.6		1.27, 1.9, 1.31
	1.8, 1.30, 1.24		1.18, 1.20, 1.7		1.28, 1.10, 1.15
	1.9, 1.29, 1.15		1.19, 1.1, 1.8		1.29, 1.11, 1.6
	1.10, 1.28, 1.16		1.20, 1.2, 1.30		1.30, 1.12, 1.17

Тема 2. Динамика материальной точки

	2.1, 2.10, 2.59		2.11, 2.20, 2.51		2.10, 2.30, 2.40
	2.2, 2.11, 2.58		2.12, 2.21, 2.50		2.11, 2.31, 2.41
	2.3, 2.12, 2.57		2.13, 2.22, 2.49		2.12, 2.32, 2.42
	2.4, 2.13, 2.56		2.14, 2.23, 2.48		2.13, 2.33, 2.43
	2.5, 2.14, 2.55		2.15, 2.24, 2.47		2.14, 2.34, 2.44
	2.6, 2.15, 2.54		2.16, 2.25, 2.46		2.15, 2.35, 2.45
	2.7, 2.16, 2.53		2.17, 2.26, 2.45		2.16, 2.36, 2.46
	2.8, 2.17, 2.52		2.18, 2.27, 2.44		2.17, 2.37, 2.47
	2.9, 2.18, 2.53		2.19, 2.28, 2.43		2.18, 2.38, 2.48
	2.10, 2.19, 2.52		2.20, 2.29, 2.42		2.19, 2.39, 2.49

Тема 3. Динамика вращательного движения