Соединение 3-х фазазных приемников «звездой» без нулевого провода.
Схема «звезда без нулевого провода». При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и ХA=ХВ=ХС), фазные токи iA, iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи iA, iB, iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю. Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209). Такая схема называется «звезда без нулевого провода». При трехпровод-ной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210). Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207). Такими же будут и соотношения между фазными и линейными токами и напряжениями: 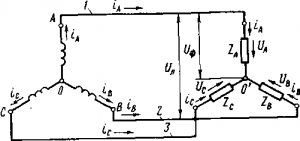
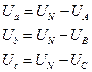
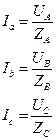
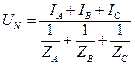
Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три.
Соединение 3-х фазных приемников «треугольником»
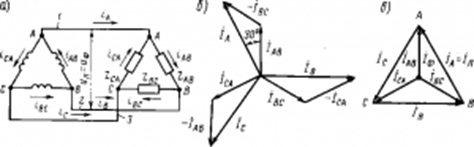
При соединении фазных обмоток источника трехфазного тока «треугольником» (рис. 211, а) конец первой фазы АВ соединяется с началом второй фазы ВС, конец второй фазы соединяется с началом третьей фазы СА и конец третьей фазы — с началом первой АВ. Три линейных провода 1, 2 и 3, идущих к приемникам электрической энергии, присоединяются к началам А, В и С этих фаз. Таким образом, в схеме «треугольник» фазные напряжения Uф равны линейным Uл и не зависят от сопротивлений ZAB, ZBC, ZCA.
Линейные токи в схеме «треугольник» согласно первому закону Кирхгофа для узлов А, В и С соответственно. линейный ток равен векторной разности соответствующих фазных токов.
IA = IAB – ICA; IB = IBC – IAB; IC = ICA – IBC 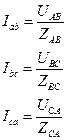
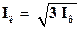
Мощность 3-х фазных цепей.
Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:
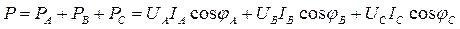 ,
,
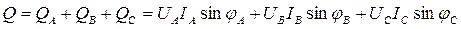 ,
,
где IA, UA, IB, UB, IC, UC – фазные значения токов и напряжений.
В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:

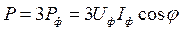 ,
,

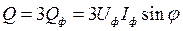 ,
,
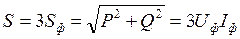 .
.
В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения 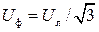 ;
; 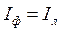 , тогда получим:
, тогда получим:
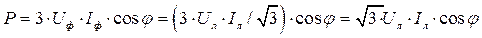 .
.
Для схемы треугольника верны соотношения: Uф=Uл ; Iф=Iл / 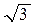 , тогда получим:
, тогда получим:
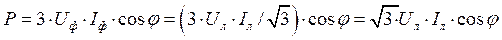
Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:
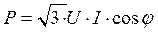 [Вт],
[Вт],
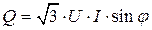 [вар],
[вар],
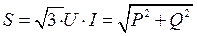 [ВА].
[ВА].
