Однородными уравнениями не являются

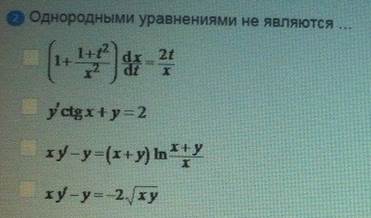ОТВЕТ 1.2.

Фундаментальную систему

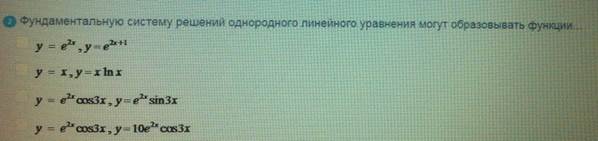
ОТВЕТ 2.3.

Для уравнения в полных

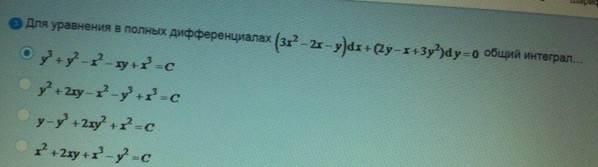
ОТВЕТ 1

Интеграл

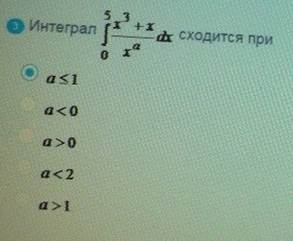ОТВЕТ 4

Значение

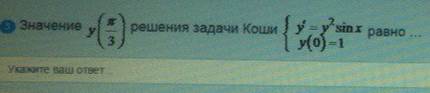ОТВЕТ 2

Интеграл

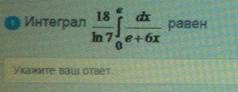ОВТЕТ 3

Объем тела

ОТВЕТ 2

Система дифференциальных уравнений

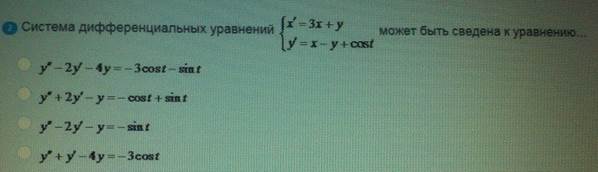
ОТВЕТ 1

Интеграл

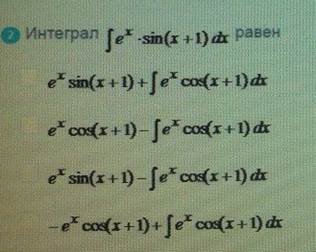ОТВЕТ 3,4

Определить с помощью какого

ОТВЕТ 3

Верными являются следующие

ОТВЕТ 1.2.5.

Для интеграла

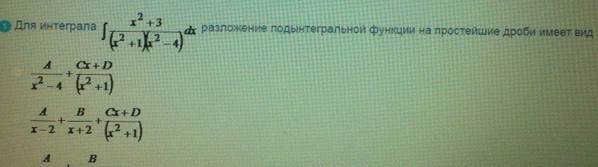
ОТВЕТ 2

Общим решением

ОТВЕТ 2

Интеграл

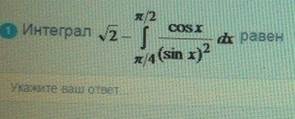ОТВЕТ 1

Если производная

ОТВЕТ 1.4.

ВАРИАНТ 4

Интеграл

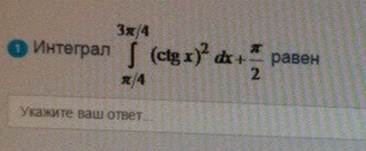ОТВЕТ 2

Для интеграла

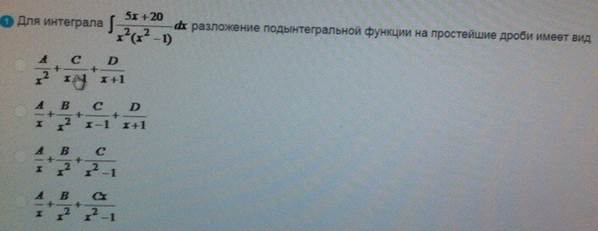
ОТВЕТ 2

Верными являются

ОТВЕТ 1.2.3.

Для уравнения в полных

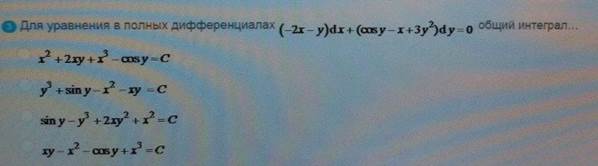
ОТВЕТ 2

Общим решением

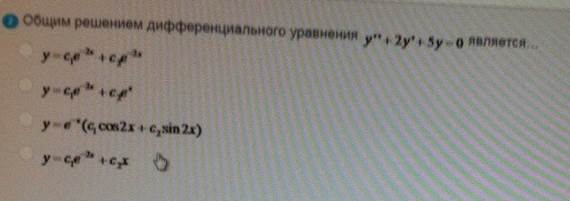
ОТВЕТ 3

Однородными уравнениями не являются

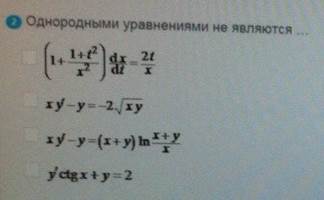ОТВЕТ 1.4.

Фундаментальную систему решений

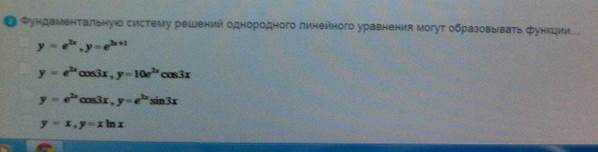
ОТВЕТ 3.4.

Интеграл

ОТВЕТ 3…..

Интеграл

ОТВЕТ 5

Определить с помощью какого интеграла

ОТВЕТ 2

Если производная

ОТВЕТ 1.2.

Объем тела, образованного

ОТВЕТ 1

ВАРИАНТ 5

Система дифференциальных

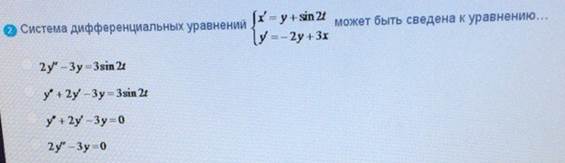
ОТВЕТ 2

Однородными уравнениями

ОТВЕТ 1.3.

Интеграл

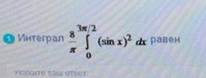ОТВЕТ 6

(ВОМ) Интеграл

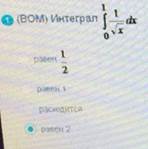ОТВЕТ 4

Интеграл

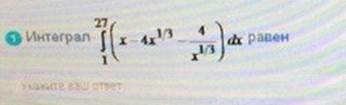ОТВЕТ 76

Верными являются следующие

ОТВЕТ 1.3.4.

Фундаментальной системой

ОТВЕТ 4

Интеграл

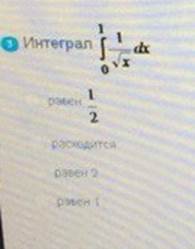ОТВЕТ 3

Объем тела, образованного

ОТВЕТ 2

Интеграл

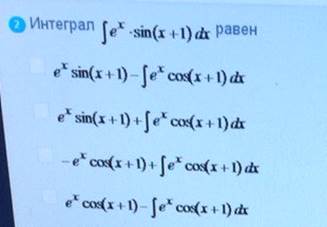ОТВЕТ 3

Для интеграла

ОТВЕТ 1

Определить с помощью какого интеграла

ОТВЕТ 1

Общим решением дифференциального

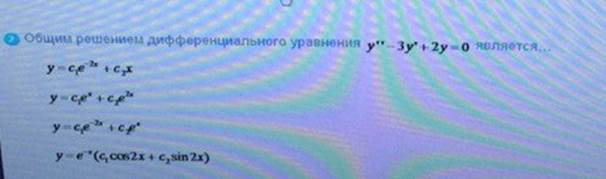
ОТВЕТ 2

Для уравнения в полных

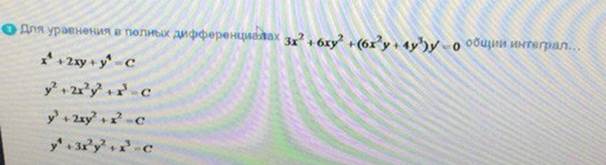
ОТВЕТ 4

Интеграл

ОТВЕТ 3

Интеграл

ОТВЕТ 3

ВАРИАНТ 6

Значение

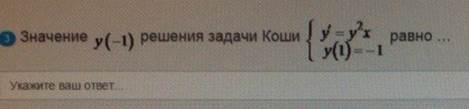ОТВЕТ -1

Система дифференциальных уравнений

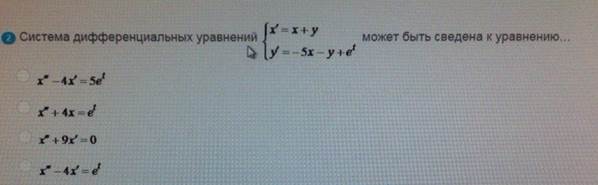
ОТВЕТ 2

Общим решением дифференциального уравнения

ОТВЕТ 2

Интеграл

ОТВЕТ 2

Интеграл

ОТВЕТ 5

Для интеграла

ОВТЕТ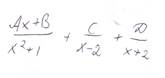

Для уравнения в полных

ОТВЕТ 3

Интеграл

ОТВЕТ 1,3

если

Если производная

Верными являются следующие

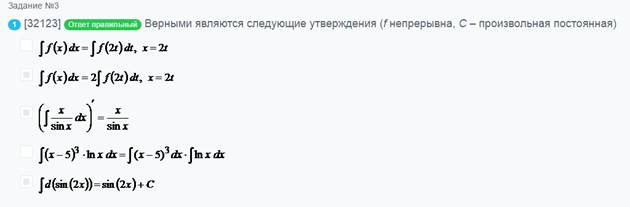
интеграл

интеграл

Определенный интеграл

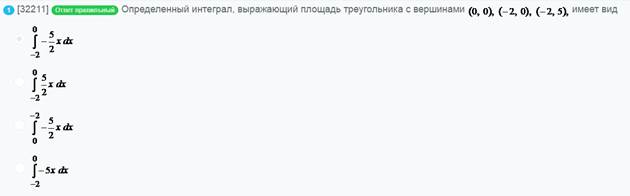
формула

интеграл

Если производная

интеграл

Для интеграла

После введения функции

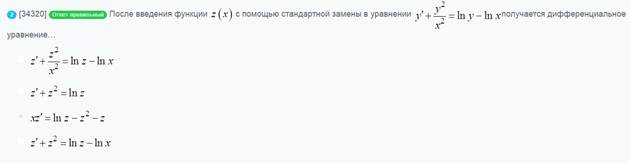
Для уравнения в полных

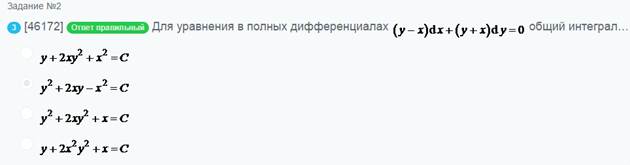
Если

Дифференциальные уравнения, упорядоченные

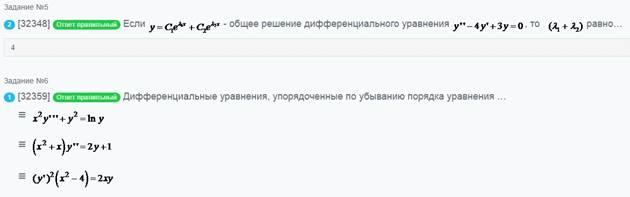
Однородное дифференциальное уравнение

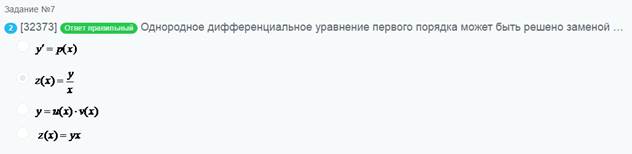
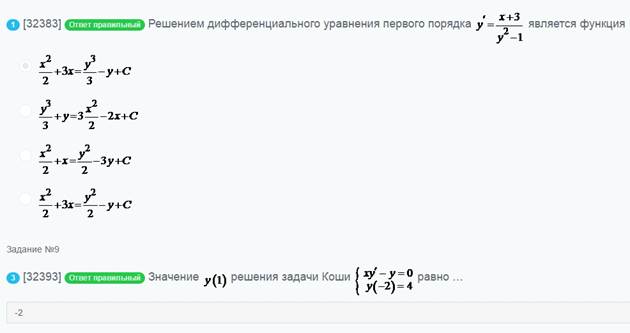
Решением дифференциального уравнения

значение

Уравнениями Бернулли

Решением дифференциального уравнения второго порядка

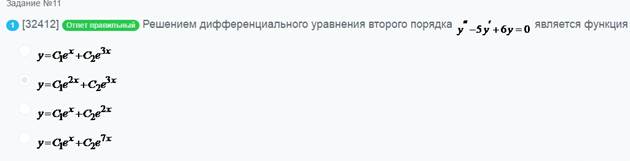
Частным решением дифференциального

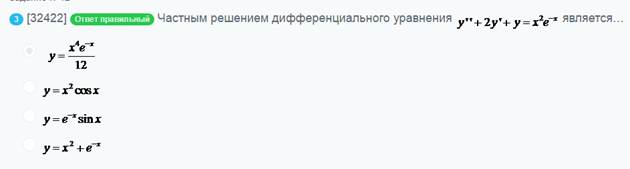
Общее решение системы дифференциальных

Система дифференциальных

Объем тела, образованного

Интеграл

интеграл

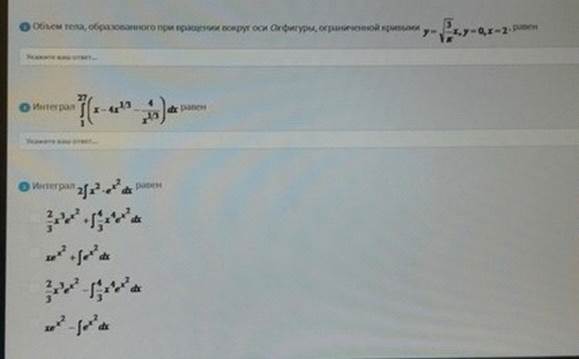
Ответы: 1)8 2)76 3)3,4

Система дифференциальных

Значение

Если функции

Ответ: 1)3 2)2 3)3

Система дифференциальных уравнений

Однородными уравнениями не являются

Интеграл

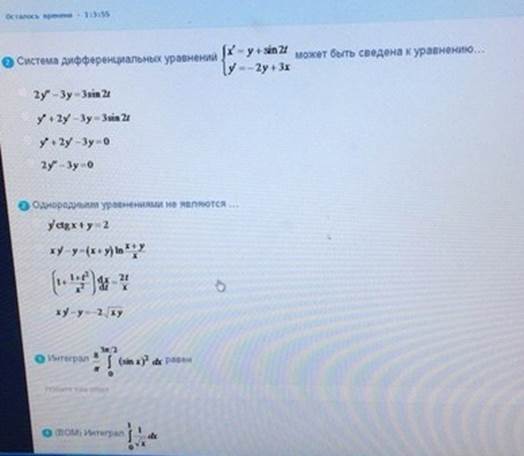
Ответ:1)2 2)2,3 3)6

Интеграл

Значение

Для интеграла

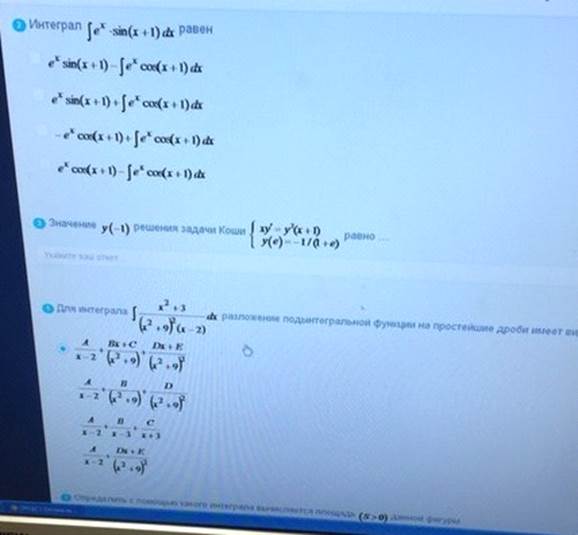
Ответ:1)1,3 2)1 3)1

Интеграл

(ВОМ) Интеграл

Значение

Если

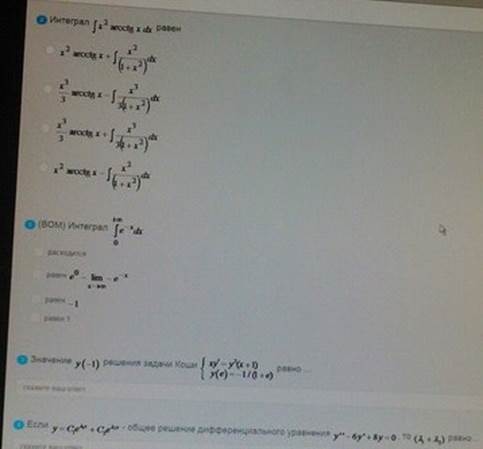
Ответ:1)2 2)1,2 3)1 4)6

Верными являются следующие

После введения функции

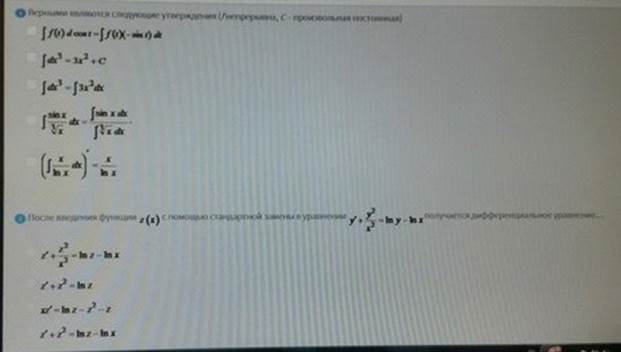
Ответ: 1)1,3 2)3

(ВОМ) Интеграл

Интеграл, Верными являются следующие

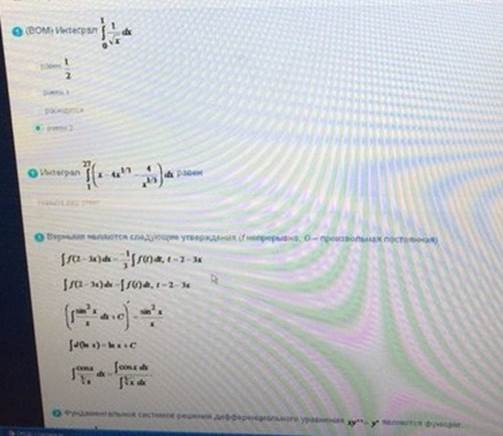
Ответ: 1)1 2)76 3)1,3,4

Общим решением дифференциального уравнения

Несобственный интеграл

Ответ: 1)4 2)1

Для интеграла

Определенный интеграл

Решением дифференциального уравнения второго порядка

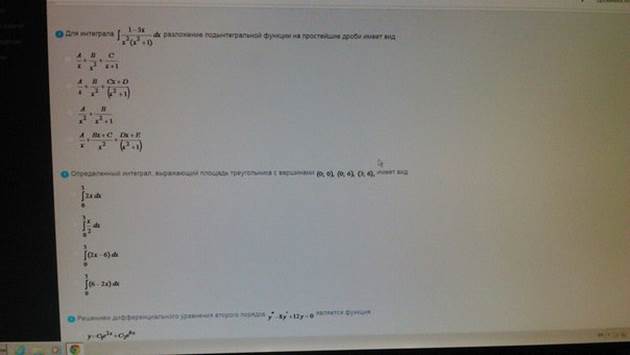
Ответ:1)2 2)4 3)1

Если

Верными являются следующие утверждения

Интеграл

Ответ:1)1 2)1,3,4 3)8

Определить с помощью какого интеграла

Оющим решением дифференциального

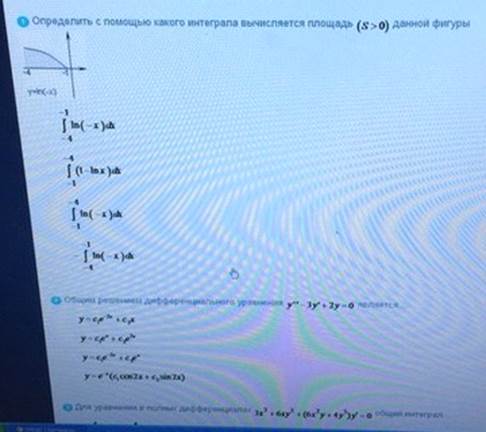
Ответ:1)1 2)2

Система дифференциальных уравнений

Значение

Интеграл

Ответ:1)1 2)1 3)2

После введения функции