Электростатическое экранирование
Понятие пространственного масштаба разделения зарядов можно уточнить, если рассмотреть электростатический потенциал вокруг отдельной заряженной частицы в плазме. В пустом пространстве вокруг частицы с зарядовым числом Z этот потенциал выражается как
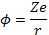 (2.1)
(2.1)
Каждая заряженная частица вызывает поляризацию окружающей плазмы: вокруг такой частицы скапливается «атмосфера» с избытком частиц противоположного знака, экранирующая поле частицы. Экранированный потенциал может быть вычислен с помощью теории Дебая, развитой первоначально для растворов сильных электролитов. Эта теория основана на представлении о так называемом самосогласованном поле: находят такое распределение электрического поля, которое создает распределение частиц, возбуждающее в свою очередь заданное поле. Для нахождения самосогласованного поля используют уравнение Пуассона
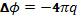 (2.2)
(2.2)
и распределение Больцмана
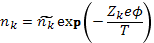 (2.3)
(2.3)
где Т — температура в энергетических единицах; nk — концентрация частиц с зарядовым числом Zk в точке с по-потенциалом φ; 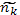 — концентрация тех же частиц в точке с нулевым потенциалом (ее приравнивают средней концентрации по всему объему). Индексом k отмечены все частицы, включая электроны, которым приписывается Z = —1. В некоторых случаях удобно выделять электроны и нумеровать индексом i только ионы. Средние концентрации
— концентрация тех же частиц в точке с нулевым потенциалом (ее приравнивают средней концентрации по всему объему). Индексом k отмечены все частицы, включая электроны, которым приписывается Z = —1. В некоторых случаях удобно выделять электроны и нумеровать индексом i только ионы. Средние концентрации 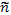 удовлетворяют условию квазинейтральности
удовлетворяют условию квазинейтральности
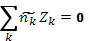 (2.4)
(2.4)
или
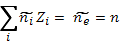 (2.5)
(2.5)
где n — концентрация электронов. Объемный заряд
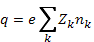 (2.6)
(2.6)
Подставив выражение (2.3) в уравнение (2.2), получим нелинейное уравнение самосогласованного поля в виде
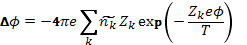 (2.7)
(2.7)
Однако в таком нелинейном виде пользоваться уравнением не имеет смысла. Дело в том, что распределение Больцмана дает вероятность нахождения частицы в точке с потенциалом φ, т. е. среднее по времени значение концентрации, но мгновенные концентрации случайным образом меняются (флуктуируют) вокруг этого среднего значения, вызывая соответствующие флуктуации потенциала. Если в уравнении (2.7) под φ подразумевать среднее по времени значение потенциала, то окажется, что в правой части среднее значение функции заменено функцией от среднего значения, что допустимо только для линейных функций. Поэтому указанное уравнение может быть использовано только в линейном приближении. Для линеаризации раскладываем в правой части уравнения (2.7) экспоненциальные функции в ряд, сохраняя только линейные члены. Члены с нулевой степенью φ, согласно условию (2.4), взаимно уничтожаются, и получается линейное уравнение самосогласованного поля в виде
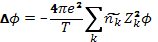 (2.8)
(2.8)
Решение для сферически симметричного распределения потенциала вокруг точечного заряда имеет вид
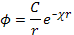 (2.9)
(2.9)
где постоянная экранирования
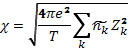 (2.10)
(2.10)
Обратная величина называется длиной экранирования или дебаевской длиной. Легко видеть, что она полу чается из введенных выше пространственных масштабов разделения зарядов dk по правилу сложения обратных квадратов:
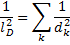 (2.11)
(2.11)
Поэтому длину экранирования можно рассматривать как масштаб разделения зарядов или поляризационную длину для всей плазмы в целом. Постоянная С в выражении по-потенциала (2.9) должна быть такой, чтобы на малых расстояниях потенциал стремился к значению, определяемому формулой (2.1). Отсюда следует окончательное выражение для экранированного, или дебаевского, потенциала вокруг заряженной частицы в плазме
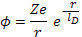 (2.12)
(2.12)
Учитывая условие (2.5), удобно формулу (2.10) представить в виде
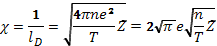 (2.13)
(2.13)
где
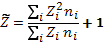 (2.14)
(2.14)
(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 1, §2)
Классификация видов плазмы
С помощью введенных понятий о дебаевской длине и плазменной частоте можно классифицировать встречающиеся в природе плазмы на разреженные и плотные, классические и квантовые. Внутренняя энергия плазмы складывается из кинетических энергий ионов и электронов и из энергии их электростатического новского взаимодействия (в плазме, нагретой до релятивистских температур, нужно учитывать и магнитное взаимодействие). Сравним среднюю кинетическую энергию (3/2)T, приходящуюся на одну частицу, со средней энергией взаимодействия. Из-за дебаевского экранирования взаимодействие заряженной частицы с далекими частицами несущественно, и надо учитывать в основном лишь ближайших соседей. Среднее расстояние до соседней частицы 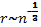 , следовательно, энергия взаимодействия приблизительно равна
, следовательно, энергия взаимодействия приблизительно равна 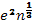 . Поэтому, как правило, плазму можно считать идеальным газом, если
. Поэтому, как правило, плазму можно считать идеальным газом, если 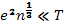 . Если обе части неравенства возвести в степень 3/2, то, как легко заметить, неравенство примет следующий вид:
. Если обе части неравенства возвести в степень 3/2, то, как легко заметить, неравенство примет следующий вид: 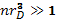 . Таким образом, условие идеальности плазмы можно записать через число частиц в объеме с размерами порядка дебаевской длины. Это число должно быть много больше единицы. При
. Таким образом, условие идеальности плазмы можно записать через число частиц в объеме с размерами порядка дебаевской длины. Это число должно быть много больше единицы. При 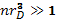 тепловая энергия частиц превышает как энергию электростатического взаимодействия, так и равновесную энергию электронных колебаний плазмы. Если указанное условие не выполнено, плазма уже не является газом, а скорее напоминает жидкость с, вообще говоря, очень сложным и до сих пор неизвестным уравнением состояния. При дальнейшем повышении плотности плазмы можно ожидать ее металлизации. При больших плотностях в плазме должны проявляться также и квантовые эффекты. Сначала их следует учитывать в ленгмюровских колебаниях. Очевидно, это должно произойти тогда, когда квант энергии плазменных колебаний станет сравнимым со средней тепловой энергией, приходящейся на один электрон. При этом условии длина волны де-Бройля для электронов со скоростями порядка средней тепловой оказывается сравнимой с дебаевским радиусом. Еще раньше, когда будет выполнено условие, т. е. длина волны де-Бройля будет сравнима со средним расстоянием между электронами, квантовой становится статистика электронов (распределение Ферми — Дирака вместо больцмановского). Это так называемая квантовая вырожденная плазма.
тепловая энергия частиц превышает как энергию электростатического взаимодействия, так и равновесную энергию электронных колебаний плазмы. Если указанное условие не выполнено, плазма уже не является газом, а скорее напоминает жидкость с, вообще говоря, очень сложным и до сих пор неизвестным уравнением состояния. При дальнейшем повышении плотности плазмы можно ожидать ее металлизации. При больших плотностях в плазме должны проявляться также и квантовые эффекты. Сначала их следует учитывать в ленгмюровских колебаниях. Очевидно, это должно произойти тогда, когда квант энергии плазменных колебаний станет сравнимым со средней тепловой энергией, приходящейся на один электрон. При этом условии длина волны де-Бройля для электронов со скоростями порядка средней тепловой оказывается сравнимой с дебаевским радиусом. Еще раньше, когда будет выполнено условие, т. е. длина волны де-Бройля будет сравнима со средним расстоянием между электронами, квантовой становится статистика электронов (распределение Ферми — Дирака вместо больцмановского). Это так называемая квантовая вырожденная плазма.
Согласно принципу Паули два электрона с одинаковыми спинами не могут находиться в одной и той же точке пространства, поэтому потенциальная энергия взаимного электростатического отталкивания электронов, а значит, и возвращающая сила в плазменных колебаниях несколько уменьшаются. Однако, поскольку обменные силы короткодействующие, они не могут изменить частоту ленгмюровских волн с бесконечной длиной волны и влияют лишь на частоту волн с конечной величиной волнового вектора.
Подавляющее большинство плазм в природе можно считать идеальным газом (космическая, газоразрядная и т. п.). Примером неидеальной плазмы могут служить сильные электролиты. Наиболее интересными из них являются растворы щелочных металлов в аммиаке, где хорошо прослеживается переход к жидкому плазменному состоянию и металлизации. Представителем квантовой плазмы молено считать электронный газ в металлах: при плотности конденсированного вещества (ne~1023 см-3) квант энергии плазменных колебаний по порядку величины оказывается равным единицам электронвольт. Квантовыми свойствами может обладать и плазма, состоящая из электронов и положительно заряженных квазичастиц — дырок в полупроводниках. Виды плазмы такого рода принято объединять под названием плазма твердого тела. Явление квантового вырождения должно иметь место и для электронного газа в очень плотном веществе звезд — белых карликов.
Свойства плазмы усложняются, если одновременно с заряженными частицами (ионами и электронами) в ней существуют также нейтральные атомы и молекулы, т. е. плазма не является полностью ионизованной.
Степень ионизации плазмы — отношение числа заряженных частиц к первоначальному числу атомов—определяется конкуренцией между процессами ионизации (развала атомов) и обратным процессом рекомбинации, т. е. воссоединения электронов и ионов в нейтральные частицы.
Общепринято также делить плазму на высоко- и низкотемпературную. Это разделение в значительной степени связано с видами конкретных исследований и их приложений. Так, с высокотемпературной плазмой связаны исследования по проблеме управляемого термоядерного синтеза. Именно эти исследования стимулировали бурный расцвет физики высокотемпературной плазмы в 50—60-х годах, позволивший объяснить многие явления в физике радиационных поясов, и в некоторых новых областях астрофизики. Низкотемпературная плазма является рабочим телом— газообразным проводником для магнитогидродинамических генераторов.
Холодную плазму в ионосфере можно рассматривать как одну из природных форм реализации низкотемпературной плазмы. Изложенную классификацию плазм удобно
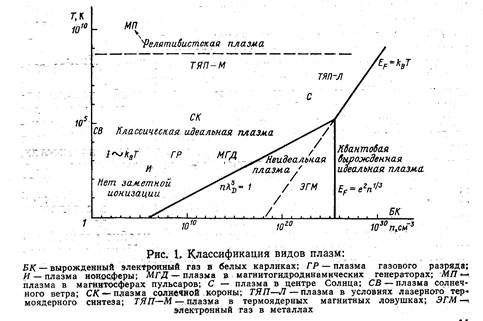
проиллюстрировать диаграммой (рис. 1.3). Поскольку интересы авторов относятся, главным образом, к большим Т, книга практически посвящена физике горячей, полностью ионизованной плазмы.
Широкое использование численных методов в физике плазмы, первоначально служившее подспорьем при анализе экспериментов, и их сопоставлении с теорией, сейчас привело к самостоятельному направлению, имеющему дело с так называемой численной плазмой. Прямые решения на быстродействующих вычислительных машинах уравнений движения N взаимодействующих заряженных частиц часто называют численными экспериментами. В некоторых случаях N удается довести до 106.
(источник:Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков, гл.1, §1.3)
2. Виды плазменных состояний. Идеальная и неидеальная плазма. Параметр вырождения. (см. 1.3) Изотермичная и неизотермичная плазма. Обобщенное понятие температуры. Газовое приближение плазмы. Частично и полностью ионизированная плазма. Степень ионизации плазмы. (см. 1.3) Замагниченная и незамагниченная плазма. Параметр ωτ. (см. 4.7) Магнитное давление.
Температура плазмы
Термодинамика изучает свойства систем, находящихся в состоянии теплового, или термического, равновесия. Важнейшей характеристикой такой системы является ее температура. Понятие температуры имеет смысл только при наличии хотя бы частичного равновесия. В статистической физике температура определяется как величина, обратно пропорциональная модулю так называемого канонического распределения. Если вероятность нахождения системы в состоянии с энергией εi пропорциональна 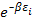 , то температура Т определяется из условия
, то температура Т определяется из условия
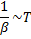 (4.1)
(4.1)
Обычно в качестве множителя пропорциональности вводится постоянная Больцмана k
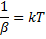 (4.2)
(4.2)
Определенная таким образом температура имеет собственную размерность: она измеряется в градусах (обычно по шкале Кельвина). В физике плазмы принято полагать множитель пропорциональности в формуле (4.1) равным единице, т. е. определять температуру как величину, обратную модулю распределения. Определенная таким образом температура имеет размерность энергии. Поэтому ее называют температурой в энергетических единицах. В дальнейшем везде, где это специально не оговорено, мы будем под температурой понимать именно температуру в энергетических единицах. Согласно закону равнораспределения энергии, она равна средней энергии, приходящейся на две степени свободы классического идеального газа. При измерении температуры в энергетических единицах вероятность состояния с энергией εi пропорциональна величине 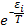 .
.
Удобной для физики плазмы энергетической единицей температуры является электронвольт (эв):
1 эв =1,6·10-12 эрг= 11600° К.
Для горячей плазмы единицей температуры часто служит килоэлектронвольт (кэв).
Плазма имеет одну определенную температуру, только если она находится в состоянии полного термодинамического равновесия. Очень часто в плазме приходится иметь дело с частичным термодинамическим равновесием. Так, обмен энергиями электронов с ионами происходит гораздо медленнее, чем обмен между частицами, близкими по массе. Поэтому в не слишком плотной плазме может длительное время существовать состояние, когда она характеризуется двумя температурами: электронной Те и ионной Тi. Плазму с Те = Ti называют изотермической. Получение ее в обычных условиях эксперимента — задача довольно сложная.
Если ускорение частиц происходит под действием электромагнитных полей или ударных волн, то может не быть и частичного равновесия. В таких случаях теряют смысл даже электронная и ионная температуры. Иногда в неравновесной плазме температурой предлагают называть среднюю энергию, приходящуюся на две степени свободы частицы. Однако в плазме с несколькими сортами ионов при этом может оказаться, что разные ионы будут иметь разные температуры.
В ударной волне все частицы набирают одинаковую скорость и, следовательно, «температура» частиц данного рода может возрастать с их массой.
(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 2, §1)
Магнитное давление
Часто плазма находится в магнитном поле, которое либо проникаетв глубь нее, либо окружает снаружи. В статическом магнитном поле на поверхность, ограничивающую магнитный поток, действует давление 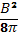 дин/см2. Обычно плазма диамагнитна, поэтому она выталкивает приложенное к ее поверхности магнитное поле. Это означает, что магнитное давление
дин/см2. Обычно плазма диамагнитна, поэтому она выталкивает приложенное к ее поверхности магнитное поле. Это означает, что магнитное давление 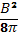 может уравновесить кинетическое давление плазмы р = nkT на границе плазма — магнитное поле. При
может уравновесить кинетическое давление плазмы р = nkT на границе плазма — магнитное поле. При 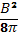 > р плазму можно сжать добольшей плотности и тем самым увеличить ее температуру.В тех случаях, когда магнитное поле проникает в плазму, часто пользуются параметром β (плазменное бета), равным отношению локальных значений давления плазмы и магнитного поля:
> р плазму можно сжать добольшей плотности и тем самым увеличить ее температуру.В тех случаях, когда магнитное поле проникает в плазму, часто пользуются параметром β (плазменное бета), равным отношению локальных значений давления плазмы и магнитного поля:
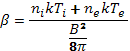 (5.1)
(5.1)
В равновесномпереходном слое на плоской границе плазма — магнитное поле условиепостоянства давления имеет вид
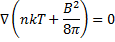 (5.2)
(5.2)
(источник:Н.Кролл, А.Трайвелпис, Основы физики плазмы, гл.1, §6)
Плазменные состояния в ранней Вселенной. Большой взрыв. Понятие о стандартной модели Вселенной. Темная материя и темная энергия. Кварк-глюонная плазма. Эпоха космической инфляции. Эпоха рекомбинации ранней Вселенной. Реликтовое излучение.
Расширяющаяся Вселенная
Имеется целый ряд фактов, говорящих о свойствах Вселенной сегодня и в относительно недалеком прошлом.
|
Вселенная в целом однородна: все области во Вселенной выглядят одинаково. Разумеется, это не относится к небольшим областям: есть области, где много звезд — это галактики; есть области, где много галактик, — это скопления галактик; есть и области, где галактик мало, — это гигантские пустоты. Но области размером 300 миллионов световых лет и больше выглядят все одинаково. Об этом однозначно свидетельствуют астрономические наблюдения, в результате которых составлена «карта» Вселенной до расстояний около 10 млрд световых лет от нас. Нужно сказать, что эта «карта» служит источником ценнейшей информации о современной Вселенной, поскольку она позволяет на количественном уровне определить, как именно распределено вещество во Вселенной.
На рис. 2 показан фрагмент этой карты, охватывающий относительно небольшой объем Вселенной. Видно, что во Вселенной имеются структуры довольно большого размера, но в целом галактики «разбросаны» в ней однородно.
Вселенная расширяется: галактики удаляются друг от друга. Пространство растягивается во все стороны, и чем дальше от нас находится та или иная галактика, тем быстрее она удаляется от нас. Сегодня темп этого расширения невелик: все расстояния увеличатся вдвоепримерно за 15 млрд лет, однако раньше темп расширения был гораздо больше. Плотность вещества во Вселенной убывает с течением времени, и в будущем Вселенная будет всё более и более разреженной. Наоборот, раньше Вселенная была гораздо более плотной, чем сейчас. О расширении Вселенной прямо свидетельствует «покраснение» света, испущенного удаленными галактиками или яркими звездами: из-за общего растяжения пространства длина волны света увеличивается за то время, пока он летит к нам. Именно это явление было установлено Э. Хабблом в 1927 году и послужило наблюдательным доказательством расширения Вселенной, предсказанного за три года до этого Александром Фридманом.
Замечательно, что современные наблюдательные данные позволяют измерить не только темп расширения Вселенной в настоящее время, но проследить за темпом её расширения в прошлом. О результатах этих измерений и вытекающих из них далеко идущих выводах мы еще будем говорить. Здесь же скажем о следующем: сам факт расширения Вселенной, вместе с теорией гравитации — общей теорией относительности — свидетельствует о том, что в прошлом Вселенная была чрезвычайно плотной и чрезвычайно быстро расширялась. Если проследить эволюцию Вселенной назад в прошлое, используя известные законы физики, то мы придем к выводу, что эта эволюция началась с момента Большого Взрыва; в этот момент вещество во Вселенной было настолько плотным, а гравитационное взаимодействие настолько сильным, что известные законы физики были неприменимы. С тех пор прошло 14 млрд лет, это — возраст современной Вселенной.
Вселенная «теплая»: в ней имеется электромагнитное излучение, характеризуемое температурой Т = 2,725 градусов Кельвина (реликтовые фотоны, сегодня представляющие собой радиоволны). Разумеется, эта температура сегодня невелика (ниже температуры жидкого гелия), однако это было далеко не так в прошлом. В процессе расширения Вселенная остывает, так что на ранних стадиях её эволюции температура, как и плотность вещества, была гораздо выше, чем сегодня. В прошлом Вселенная была горячей, плотной и быстро расширяющейся.
Вселенная в прошлом
Обсудим два этапа эволюции Вселенной, о которых сегодня имеются надежные наблюдательные данные. Один из них, относительно недавний — это этап перехода вещества во Вселенной из состояния плазмы в газообразное состояние. Это произошло при температуре 3000 градусов, а возраст Вселенной к тому моменту составлял 300 тыс. лет (совсем немного по сравнению с современными 14 млрд лет). До этого электроны и протоны двигались отдельно друг от друга, вещество представляло из себя плазму. При температуре 3000 градусов произошло объединение электронов и протонов в атомы водорода, и Вселенная оказалась заполненной этим газом. Важно, что плазма непрозрачна для электромагнитного излучения; фотоны всё время излучаются, поглощаются, рассеиваются на электронах плазмы. Газ, наоборот, прозрачен. Значит, пришедшее к нам электромагнитное излучение с температурой 2,7 градуса свободно путешествовало во Вселенной с момента перехода плазма—газ, остыв (покраснев) с тех пор в 1100 раз из-за расширения Вселенной. Это реликтовое электромагнитное излучение сохранило в себе информацию о состоянии Вселенной в момент перехода плазма—газ; с его помощью мы имеем фотоснимок (буквально!) Вселенной в возрасте 300 тыс. лет, когда её температура составляла 3000 градусов.
Измеряя температуру этого реликтового электромагнитного излучения, пришедшего к нам сразных направлений на небе, мы узнаём, какие области были теплее или холоднее (а значит, плотнее или разреженнее), чем в среднем по Вселенной, а главное — насколько они были теплее или холоднее. Результат этих измерений состоит в том, что Вселенная в возрасте 300 тыс. лет была гораздо более однородной, чем сегодня: вариации температуры и плотности составляли тогда менее 10–4 (0,01%) от средних значений. Тем не менее, эти вариации существовали: с разных направлений электромагнитное излучение приходит с несколько различной температурой. Это показано на рис. 3, где изображено распределение температуры по небесной сфере (фотоснимок ранней Вселенной) за вычетом средней температуры 2,725 градусов Кельвина; более холодные области показаны синим, более теплые — красным цветом.
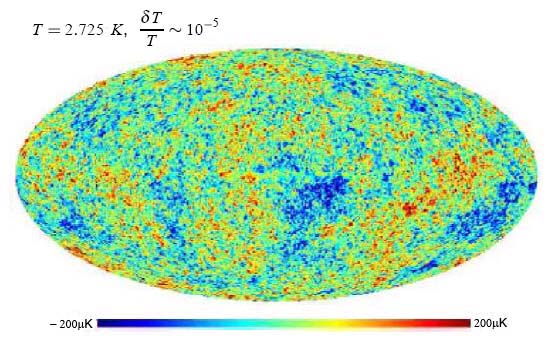
Фотоснимок, изображенный на рис. 3, привел к нескольким важным и неожиданным выводам. Во-первых, он позволил установить, что наше трехмерное пространство с хорошей степенью точности евклидово: сумма углов треугольника в нем равна 180 градусов даже для треугольников со сторонами, длины которых сравнимы с размером видимой части Вселенной, т. е. сравнимы с 14 млрд световых лет. Вообще говоря, общая теория относительности допускает, что пространство может быть не евклидовым, а искривленным; наблюдательные же данные свидетельствуют, что это не так (по крайней мере, для нашей области Вселенной). Способ измерения «суммы углов треугольника» на космологических масштабах расстояний состоит в следующем. Можно надежно вычислить характерный пространственный размер областей, где температура отличается от средней: на момент перехода плазма—газ этот размер определяется возрастом Вселенной, т. е. пропорционален 300 тыс. световых лет. Наблюдаемый угловой размер этих областей зависит от геометрии трехмерного пространства, что и дает возможность установить, что эта геометрия — евклидова.
В случае евклидовой геометрии трехмерного пространства общая теория относительности однозначно связывает темп расширения Вселенной с суммарной плотностью всех форм энергии, так же как в ньютоновской теории тяготения скорость обращения Земли вокруг Солнца определяется массой Солнца. Измеренный темп расширения соответствует полной плотности энергии в современной Вселенной
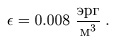
В терминах плотности массы (поскольку энергия связана с массой соотношением Е = mс2) это число составляет
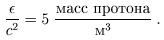
Если бы энергия во Вселенной целиком определялась энергией покоя обычного вещества, то в среднем во Вселенной было бы 5 протонов в кубическом метре. Мы увидим, однако, что обычного вещества во Вселенной гораздо меньше.
Во-вторых, из фотоснимка рис. 3 можно установить, какова былавеличина(амплитуда)неоднородностейтемпературы и плотности в ранней Вселенной — она составляла 10–4–10–5от средних значений. Именно из этих неоднородностей плотности возникли галактики и скопления галактик: области с более высокой плотностью притягивали к себе окружающее вещество за счет гравитационных сил, становились еще более плотными и в конечном итоге образовывали галактики.
Поскольку начальные неоднородности плотности известны, процесс образования галактик можно рассчитать и результат сравнить с наблюдаемым распределением галактик во Вселенной. Этот расчет согласуется с наблюдениями, только если предположить, что помимо обычного вещества во Вселенной имеется другой тип вещества — темная материя, вклад которой в полную плотность энергии сегодня составляет около 25%.
Другой этап эволюции Вселенной соответствует еще более ранним временам, от 1 до 200 секунд (!) с момента Большого Взрыва, когда температура Вселенной достигала миллиардов градусов. В это время во Вселенной происходили термоядерные реакции, аналогичные реакциям, протекающим в центре Солнца или в термоядерной бомбе. В результате этих реакций часть протонов связалась с нейтронами и образовала легкие ядра — ядра гелия, дейтерия и лития-7. Количество образовавшихся легких ядер можно рассчитать, при этом единственным неизвестным параметром является плотность числа протонов во Вселенной (последняя, разумеется, уменьшается за счет расширения Вселенной, но её значения в разные времена простым образом связаны между собой).
Сравнение этого расчета с наблюдаемым количеством легких элементов во Вселенной приведено на рис. 4: линии представляют собой результаты теоретического расчета в зависимости от единственного параметра — плотности обычного вещества (барионов), а прямоугольники — наблюдательные данные. Замечательно, что имеется согласие для всех трех легких ядер (гелия-4, дейтерия и лития-7); согласие есть и с данными по реликтовому излучению (показаны вертикальной полосой на рис. 4, обозначенной СМВ — CosmicMicrowaveBackground). Это согласие свидетельствует о том, что об 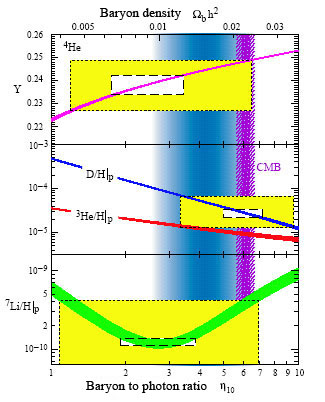 щая теория относительности и известные законы ядерной физики правильно описывают Вселенную в возрасте 1–200 секунд, когда вещество в ней имело температуру миллиард градусов и выше. Для нас важно, что все эти данные приводят к выводу о том, что плотность массы обычного вещества в современной Вселенной составляет
щая теория относительности и известные законы ядерной физики правильно описывают Вселенную в возрасте 1–200 секунд, когда вещество в ней имело температуру миллиард градусов и выше. Для нас важно, что все эти данные приводят к выводу о том, что плотность массы обычного вещества в современной Вселенной составляет
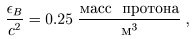
т. е. обычное вещество вкладывает всего 5% в полную плотность энергии во Вселенной.

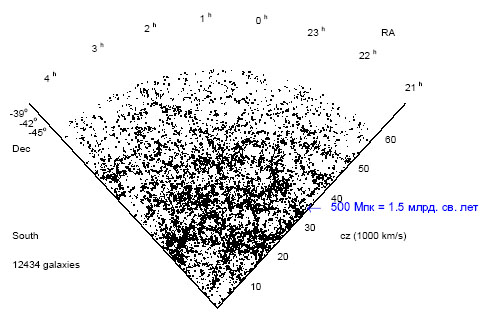 Рис. 2
Рис. 2