Работа и теплота. Первое начало термодинамики
Внутренняя энергия газа (и другой термодинамической системы) может изменяться в основном за счет двух процессов: совершения над газом работы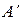 
и сообщением ему количества тепла Q . Так как состояние газа может одинаково изменяться от совершенной над ним работы 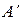и сообщенного ему количества тепла Q , то работа и теплота являются эквивалентными формами передачи энергии. Теплота - это форма передачи энергии на уровне микроскопических процессов, когда, например, молекулы газа, соударяясь с разогретыми стенками (молекулами) сосуда, получают от них дополнительную кинетическую энергию. Работа над газом - это передача энергии в форме макропроцессов. Когда поршень, перемещаясь в некотором цилиндре, сжимает газ, то молекулам газа за счет движения поршня передается дополнительная энергия и газ нагревается.
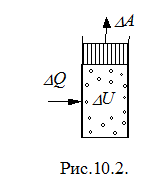Исторически развитие термодинамики было связано с необходимостью теоретического объяснения работы теплового двигателя. При сжигании топлива выделялось определенное количество тепла, и некоторая часть его DQ (рис.10.2) передавалась рабочему телу (обычно газу). Газ нагревался, и его внутренняя энергия увеличивалась на величину DU. Расширяясь, газ совершал работу DA. Отсюда принято считать DQ > 0, когда термодинамическая система получает тепло, иDA > 0 , когда эта система совершает работу. Огромная совокупность опытных фактов с учетом законов сохранения показывала, что в термодинамической системе, в которой протекают тепловые и механические процессы, всегда должно выполняться равенство
DQ = DU + DA . (10.3)
Уравнение (10.3) представляет собой содержание первого начала(закона) термодинамики. Словами его можно выразить следующим образом: количество тепла DQ , сообщенное системе, идет на приращение внутренней энергии системы DU и на совершение системой работы DA над внешними телами.
Следует отметить, что в равенстве (10.3) величина U является функцией состояния и однозначно определяется термодинамическими параметрами состояния. Величины Q и A не есть функции состояния. Они зависят не только от начального и конечного состояния системы, но и от пути изменения ее состояния.
Из равенства (10.3) следует, что единицей измерения тепла служит джоуль.
Работа газовых изопроцессов
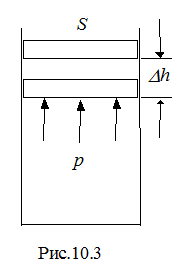Пусть газ заключен в цилиндрический сосуд, закрытый плотно пригнанным и легко скользящим поршнем (рис.10.3). При расширении газ будет совершать работу DA = FDh , где F - сила, с которой газ действует на площадь поршня S; Dh - перемещение поршня при расширении газа. Приращение объема газа DV = SDh . Подставляя силу F = pS и DV в выражение для работы, получим DA = pDV . При расширении газа работа будет положительной, при сжатии - отрицательной. Если давление газа при совершении работы изменяется, то находят работу при каждом элементарном изменении объема
dA = pdV (10.4)
суммируют все элементарные работы для этого газового процесса. Полная работа
A =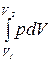 
, (10.5)
где V1 - начальный объем газа, V2 - его конечный объем. Применим формулу (10.5) для расчета работы изопроцессов.
1. Рассмотрим изохорический процесс. Для этого процесса объем газа V = const , dV = 0 и A = 0 . Газ не совершает работу. Первое начало термодинамики (10.3) будет иметь вид DQ = DU , т.е. все тепло, сообщенное газу, пойдет на его нагревание.
2. Рассмотрим изобарический процесс. Так как давление не изменяется, то его как постоянную величину можно вынести из под знака интеграла (10.5). Получим A = p(V2 - V1) или с учетом уравнения Менделеева-Клапейрона pV = (m /m)RT , записанного для начального и конечного состояний, получим выражение для работы изобарического процесса
A = (m /m)R(T2 - T1). (10.6)
3. Рассмотрим изотермический процесс. Так как температура постоянна, то внутренняя энергия идеального газа не изменяется: DU = 0 . Первое начало термодинамики (10.3) будет иметь вид DQ = DA, т.е. все тепло, подведенное к системе, будет затрачено на совершение ею работы. Используя уравнение состояния идеального газа (10.6) и учтя, что T = const , запишем выражение (10.5) для работы изотермического процесса в виде
A = 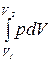= (m /m)RT 
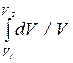= (m /m)RT ln(V2 /V1). (10.7)