Напряженность гравитационного поля. Потенциал гравитационного поля.

Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, помещенное в него другое тело оказывается под действием силы. Об «интенсивности» гравитационного поля можно судить по величине силы, действующей в данной точке на тело единичной массы. В соответствии с этим величину называют напряженностью гравитационного поля. Итак,

ОПРЕДЕЛЕНИЕ: Напряженность гравитационного поля – это величина численно равная силе, действующей на тело единичной массы.

Размерность совпадает с размерностью ускорения. Вблизи Земли напряженность поля тяготения равна ускорению свободного падения (“g”).

Из закона всемирного тяготения:

, (6.3)

– орт радиус-вектора, проведенного из материальной точки в данную точку поля; r – модуль этого радиус-вектора; m – масса тела, которое создает поле.

Каждой точке поля, создаваемого материальной точкой m соответствует определенное значение потенциальной энергии, которой обладает в этом поле материальная точка m¢. Поэтому поле можно характеризовать потенциальной энергией ( ). А величину – называют потенциалом гравитационного поля. Потенциал в данной точке поля численно равен работе сил тяготения по перемещению тела единичной массы из данной точки поля в бесконечность.

Потенциал скалярная величина, характеризующая поле с энергетической точки зрения.

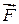Напряженность поля ( ) – векторная величина, называется силовой характеристикой поля. Направления и совпадают.

Работа сил тяготения была рассчитана ранее:

САМОСТОЯТЕЛЬНО:

Космические скорости.

ЛЕКЦИЯ 9

Основы теории относительности.

Принцип относительности.

В разд. 2.1. для механических систем был сформулирован следующий принцип относительности: во всех инерциальных системах отсчета все законы механики одинаковы. Никакими (механическими) опытами, проведенными в замкнутой инерциальной системе, нельзя об наружить, покоится система или прямолинейно и равномерно движется.

Пусть система движется относительно инерциальной системы K с постоянной скоростью v_о(рис. 7.1) так, чтобы оси x и при движении совпадали, а оси y, и z , были параллельны друг другу,причем вектор, соединяющий начала координат, r_о = v_ot , где t время. Связь между координатами этих систем описывается преобразованиями Галилея :

x = + v_o ; y = ; z = ; t = , (7.1)

где время в подвижной системе координат. Последнее равенство отражает тот факт, что согласно представлениям классической механики ход времени не зависит от относительного движения систем отсчета. Если подставить преобразования (7.1) в законы Ньютона, то эти законы превращаются в такие же законы, но в штрихованной системе отсчета. Поэтому, проделав любые опыты по механике в замкнутой инерциальной системе, и нельзя сказать, движется система или нет.

Результат исследований явлений электричества и магнетизма позволил ученому Максвеллу получить уравнения, которые сводят воедино электричество, магнетизм, свет. Однако уравнения Максвелла не подчиняются принципу относительности: если преобразовать их подстановкой типа (7.1), то их вид не останется прежним. Отсюда следует вывод, что оптические и электрические явления можно использовать для определения скорости замкнутой системы относительно некоего “мирового неподвижного эфира”. Например, скорость автомобиля равна 1 10⁸ м/с, а скорость света 3 10⁸ м/с, тогда свет от фар будет удаляться со скоростью 2 10⁸ м/с и, измерив скорость света, испускаемого фарами, можно было бы узнать скорость автомашины. Такую попытку определить абсолютную скорость орбитального движения Земли сквозь воображаемый “эфир” проделал в 1887 г. ученый Майкельсон с помощью очень чувствительного светового интерферометра. Однако результат опыта был отрицательный: “мировой эфир” оказался неуловимым. Объяснить отрицательный результат опыта Майкельсона удалось ученому Эйнштейну путем отказа от некоторых представлений классической механики.

7.2. Постулаты специальной (частной) теории относительности. Преобразования Лоренца

Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности:

1. Физические явления во всех инерциальных системах отсчета протекают одинаково. Никакими физическими опытами, проведенными внутри замкнутой инерциальной системы отсчета, нельзя обнаружить, покоится ли эта система или движется равномерно и прямолинейно.

2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника света или наблюдателя.

Наличие этих постулатов позволяет получить новые преобразования координат, отличающиеся от (7.1).

Пусть система движется относительно инерциальной системы K с постоянной скоростью v_о(рис. 7.1) так, чтобы оси x и при движении совпадали, а оси y, и z, были параллельны друг другу,причем вектор, соединяющий начала координат, , где t время. Можно показать, что координаты y и z связаны формулами y = ; z = . Ищем зависимость между подвижными и неподвижными координатами x в виде

, (7.2)

где a искомый коэффициент. Согласно первому постулату в силу равноправия систем отсчета для перехода от неподвижной системы отсчета к подвижной зависимость между координатами должна иметь аналогичный вид и отличаться лишь знаком для скорости v_o:

= a(x - v_o, t). (7.3)

Пусть в моменты времени t = = 0 в точке x = = 0 в направлении оси x испускается вспышка света. Это событие через время t будет наблюдаться в точке x = ct и через время в точке = c . Здесь используется тот факт, что скорость света c для вакуумасогласно 2^му постулату Эйнштейна одинакова в обеих системах. Подставляя в два последних равенства выражения (7.2) и (7.3), получим a(c + v_o) = ct ; a(c - v_o)t = c . Перемножая эти два равенства, получим a = 1/(1 - b ²)^0,5 , где величину b = v_o /c называют относительной скоростью.

Исключая из равенств (7.2) и (7.3) координату x, получим

t = /a + b /ac

Подставляя в эту формулу и в формулу (7.2) выражения для a и b, получим окончательно формулы для связи координат и времени :

(7.4)

Полученные формулы называют преобразованиями Лоренца. Ученый Лоренц впервые получил эти формулы и показал, что если уравнения Максвелла преобразовать подстановкой (7.4), то их вид останется прежним и эти уравнения подчиняются принципу относительности. Эйнштейн предположил, что все физические законы не должны меняться от преобразований Лоренца.

Преобразования Лоренца при малых скоростях движения (b ® 0) переходят в преобразования Галилея, которые являются предельным случаем преобразований Лоренца. Из преобразований Лоренца следует, что как пространственные, так и временные преобразования не являются независимыми. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.

Теорию относительности часто называют релятивистской теорией, а специфические явления, описываемые этой теорий, - релятивистскими эффектами.

7.3. Следствия из преобразований Лоренца.

Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.

Длительность событий в разных системах отсчета. Пусть в некоторой точке , покоящейся относительно подвижной системы , происходит событие, длительность которого = - , где и - начальный и конечный промежутки времени. C помощью формул (7.4) получим, что длительность этого же события в неподвижной системе отсчета K равна

или

(7.5)

Из последнего равенства следует, что , т.е. для подвижной системы отсчета событие будет происходить за меньший промежуток времени. Следовательно, для подвижной системы отсчета время идет медленнее. Этот удивительный результат можно понять, если придумать специальные часы, в которых роль маятника играет световой сигнал, бегающий между двумя параллельными зеркалами, находящимися на расстоянии L. Период таких часов для системы отсчета, в которой они покоятся = 2L /с. Если эти часы движутся со скоростью v_o вдоль оси x (рис. 7.2), то для неподвижного наблюдателя траектория движения луча выглядит в виде зигзага и расстояние, пройденное светом за период часов t , будет более длинным, его квадрат равен 4L² + t² = с²t² . Исключая L из двух последних равенств, легко получить выражение (7.5) t = /(1-- b ²)^0,5. Если космонавт улетит от Земли со скоростью, близкой к скорости света (например, b ² = 1 - 10^-4 ), и вернется обратно через год, то по земным часам полет продлится 100 лет. Космонавт возвратится на Землю в сто раз более молодым, чем его брат-близнец. Данный результат мысленного эксперимента кажется неправильной интерпретацией преобразований Лоренца, так как, если за неподвижную систему отсчета считать движущийся корабль, то его близнец на Земле удаляется с такой же скоростью, и его время как бы замедлится по сравнению с часами на корабле. Однако эти две системы – не равнозначны, космонавт на корабле должен ускоряться и замедляться, чтобы вернуться на Землю. Поэтому система отсчета, связанная с кораблем ‑ неинерциальна. Получается, что причина замедления физических процессов связана с тем, что космонавт при путешествии подвергался дополнительным механическим перегрузкам. Детальный расчет, выходящий за рамки специальной теории относительности, показывает, что часы, движущиеся с ускорением, идут медленнее, поэтому при возвращении отстанут именно они.

Эффект замедления хода часов получил экспериментальное подтверждение при исследовании частиц m-мезонов, образующихся в космических лучах. Среднее время жизни неподвижных m-мезонов составляет 2 10^-6с. Казалось бы, что двигаясь со скоростью света m-мезоны могут пройти расстояние 600м. Однако m-мезоны проходят расстояние 20-30 км и достигают земной поверхности, т.е. для земного наблюдателя время жизни m-мезонов оказывается гораздо большим.

Одновременность событий в разных системах отсчета. Пусть в подвижной системе в точках с координатами и происходят одновременно два события в момент времени = = b . Согласно формулам (7.4) в системе K этим событиям будут соответствовать координаты t₁ = (b + v_o /c²)/(1- - b ²)^0,5 и t₂ = (b + v_o /c²)/(1-b ²)^0,5 . Из написанных формул видно, что если события в системе K пространственно разобщены ( ¹ ), они не будут происходить одновременно. Например, при > получим t₁ > t₂ , т.е. событие в точке 1 для неподвижной системы отсчета произойдет раньше, хотя для подвижной системы эти события одновременны.

Длина тел в разных системах отсчета. Из преобразований (7.4) следует, что при движении тел их размеры по осям x и y не изменяются. Пусть в системе K покоится стержень, параллельный оси x . Длина его, измеренная в этой системе, равна l = x₂ - x₁ , где x₁ и x₂ - координаты обоих концов стержня в системе K . Используя преобразования Лоренца (7.4), выразим длину стержня в следующем виде l = ( + v_o )/(1- b ²)^0,5 - ( + + v_o )/(1- b ²)^0,5 = ( - )/(1-b ²)^0,5 , где и - координаты концов стержня, измеренные в подвижной системе в один и тот же момент времени . Длина стержня в системе равна = - . Окончательно получим l = /(1- b ²)^0,5 или = l(1- b ²)^0,5 . Отсюда следует l > . Длину l называют собственной длиной стержня в той системе отсчета, в которой он покоится. Это наибольшая длина стержня. Если предмет начинает двигаться, его размеры в направлении оси x сокращаются пропорционально (1- b ²)^0,5 . Например, если неподвижное тело является шаром, то при движении шар сжимается вдоль оси x , приобретая форму эллипсоида вращения.

Релятивистский закон сложения скоростей.Пусть опять система движется относительно системы K со скоростью v_o вдоль оси x . Пусть v_x = dx/dt есть компонента скорости некоторой частицы в системе K , а = - компонента скорости ее в системе . Дифференцируя формулы (7.4), получим

; dy = d ; dz = dz’; .

Разделив первые три равенства на четвертое и учитывая, что b = v_o/c, находим

(7.6)

где v_x , v_y , v_z - составляющие скорости частицы в системе K , , , - составляющие скорости частицы в системе . Полученные формулы и определяют преобразование скоростей. При с ® релятивистские формулы переходят в формулы классической механики.

Пусть корабль движется вдоль оси x со скоростью = c / 2 и некоторая частица движется в этом же направлении относительно корабля со скоростью = c / 2 . По формулам (7.6) получим v_x = 4c/5 , т.е. по теории относительности 1/2 и 1/2 дают не 1, а 4/5.

Возьмем предельный случай. Положим, что человек на борту корабля наблюдает, распространение света вдоль оси x , т.е. = с. Тогда по формулам (8.6) получим v_x = (с + )/(1 + c/c²) = c . Итак, скорость света для неподвижного наблюдателя опять равна скорости света.

Интервал между событиями.

В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и временем, когда оно произошло. Событие можно изобразить точкой в воображаемом четырехмерном пространстве, на осях которого три пространственные координаты и время. Эти точки называются мировыми точками. Всякой частице соответствует некоторая линия (мировая линия).

В классической физике при переходе от одной системы координат к другой координаты точек изменяются, но неизменным остается расстояние между двумя выбранными точками Dl, которое можно определить из формулы Dl² = (x₂ - x₁ )² + (y₂ -y₁)² + (z₂ - z₁ )², где x₁ , y₁ , z₁ , x₂ , y₂ , z₂ - координаты точек. В теории относительности при переходе от одной системы к другой расстояние между точками не остается постоянным, т.е. не является инвариантом. Инвариантом, не зависящим от выбранной системы координат, является интервал между событиями Ds, который определяется по формуле Ds² = c²t² - Dl² . С формальной математической точки зрения интервал можно рассматривать как расстояние между мировыми точками в воображаемом четырехмерном пространстве.

Если Ds² > 0, то интервал называют времениподобным,и существует такая система отсчета. в которой оба события произошли в одной точке. Два события могут быть причинно связаны друг с другом только в том случае, если интервал между ними времениподобный.

Если Ds² < 0, то интервал называют пространственноподобным,и сущес-твует такая система отсчета, в которой оба события произошли в одно и тоже время.

Теория относительности сформулировала новое представление о пространстве и времени, показав, что пространство и время органически связаны между собой и образуют единую форму существования материи. Дальнейшее развитие теории относительности (общая теория относительности) показало, что свойства пространства-времени определяются действующими в данной области полями тяготения, и изменяются в зависимости от концентрации в пространстве массы вещества.

ЛЕКЦИЯ 10

Колебания.

Общие сведения.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости или такое движение, при котором система многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот возврат осуществляется через равные промежутки времени, то колебания называются периодическими.

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Здесь мы будем рассматривать механические колебания.

Колебания широко распространены в природе и технике. Во многих случаях они играют отрицательную роль (колебания моста, вибрации корпуса корабля, вибрации крыльев самолета и т.п.). В подобных случаях задача состоит в том, чтобы предотвратить возникновение колебаний.

Вместе с тем колебательные процессы лежат в самой основе различных отраслей техники. Так, например, на колебательных процессах основана вся радиотехника.

ПРИМЕРЫ колебательных движений: вибрация струны, движение поршня, суточные и годичные изменения температуры воздуха, морские приливы-отливы, биение сердца, тепловое движение ионов кристаллической решетки твердого тела, переменный ток и его электромагнитное поле, движение электронов в атоме и т.д.

Всевозможные колебательные движения имеют два общих характерных признака:

1. До начала колебаний и после их окончания тело находится в положении равновесия;

2. Наличие силы, которая возникает, как только тело выходит из положения равновесия. Эта сила пропорциональна смещению и направлена в сторону, противоположную смещению тела (направлена к положению равновесия). Для такой силы справедливо . Называется такая сила упругой силой. Под действием такой силы, например, может сжиматься и разжиматься пружина.

Но может случиться, что сила иного происхождения обнаруживает такую же закономерность.

Рассмотрим колебания математического маятника (рис. 8.1).

Отклоним маятник на некоторый угол j от положения равновесия и разложим силу тяжести на две составляющие:

- P_t – перпендикулярную нити;

- P_n – параллельную нити.

Под действием силы P_t шарик будет стремиться вернуться в положение равновесия. P_t=P·sinj. При малых углах sinj @ j и тогда Pt=-m·g·j. Знак «-», т.к. сила P_t препятствует возрастанию угла j. Сила P_t не упругая сила, но по своему действию и характеру аналогична упругой силе. Такая сила называется квазиупругой силой.

Несмотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими (от греческого “гармоникс” – стройный).